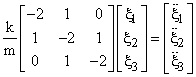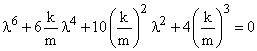|
Gravity, Entropy, and Coherence |
|
|
|
The second law of thermodynamics holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equations - then so much the worse for Maxwell's equations. If it is found to be contradicted by observation, well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation. |
|
Arthur Eddington |
|
|
|
Given a quantity of gas initially concentrated in a small region, the gas will naturally tend to expand to fill a progressively larger volume of space. This is an example of how the entropy of physical systems tends to increase. It is called an irreversible process, because a concentrated region of gas will spontaneously disperse, whereas the reverse does not normally occur, i.e., a dispersed quantity of gas will not spontaneously become concentrated into a smaller region… or will it? In the treatment of small quantities of gas the gravitational attraction of the gas molecules on each other is negligible, but for a sufficiently large quantity of gas – such as in some regions of interstellar space – there exist large enough regions of gas (of sufficient density) that a cloud of gas will naturally contract due to the mutual gravitational attraction of the molecules. Indeed this is (presumably) how stars are formed. Does the spontaneous contraction of a cloud of gas due to gravity violate the second law of thermodynamics? In other words, does entropy decrease as a result of the gravitational contraction? |
|
|
|
Consider two perfectly inelastic lumps of clay, each of mass m and temperature T0, initially at rest and separated by a distance L in an isolated region of space. The initial potential energy is V, the initial kinetic energy is K = 0, and the initial thermal energy is some function U(T0) of the temperature. The mutual gravitational attraction will cause the two lumps of clay to accelerate toward each other, and eventually collide. During the period of free-fall, potential energy is converted to kinetic energy, and when the collision takes place the kinetic energy is converted into thermal energy. So the initial state consisted of two relatively cool lumps of clay at rest and separated by a distance L, and the final state consists of a single lump of clay at rest with a higher temperature. |
|
|
|
From the initial state to the instant just prior to the collision, the process is clearly reversible. For example, if the objects were perfectly elastic, they would bounce off each other, and return to the initial state. Another possibility is if the objects have shapes (such as a ball and a torus) that allow them to pass through each other without making contact, so they would oscillate by exchanging positions. A third possibility is for the system to possess a small amount of angular momentum, so instead of falling directly together, the two objects are in highly elongated elliptical orbits about their center of mass. In all three of these cases the process has the characteristics of reversibility, as it very promptly and periodically recurs to its original state. There is no secular change. |
|
|
|
In contrast, the original scenario of two perfectly inelastic lumps of clay leads very quickly to an irrevocable change, because we cannot see how the final combined lump of warm clay could ever spontaneously recur to the initial state consisting of two separate cool lumps of clay. Clearly the final collapsed and heated state has higher entropy than the initial state, and the increase in entropy occurred not during the gravitational free-fall as potential energy is converted into kinetic energy, but during the collision, as kinetic energy is converted into thermal energy (heat). It’s worthwhile to examine this process in more detail, to understand clearly how this conversion takes place, and why it is irreversible – despite the fact that the elementary physical interactions are all explicitly reversible. We will find that an increase in entropy corresponds to a loss of coherence. |
|
|
|
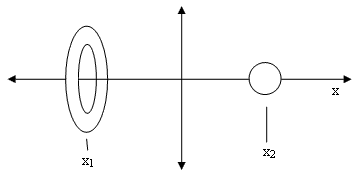
First, consider two solid objects, a ball and ring, of equal masses, initially at rest on the x-axis, equidistant from x = 0, as shown below. |
|
|
|
|
|
|
|
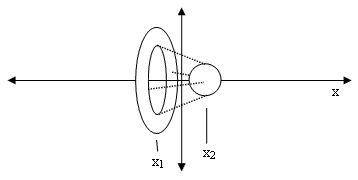
The mutual gravitational attraction of the two objects will cause them to accelerate toward each other, and they will pass each other at x = 0, and then their inertias will carry them on until they are slowed to rest again due to their mutual gravity, having exchanged places. They will continue to oscillate in this way, periodically recurring to their initial state, so we deem this process to be reversible, with constant entropy. |
|
|
|
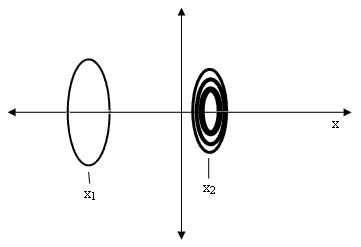
Now suppose there is a harness attached to the ring by some springs, and on one of the transits of the ball through the ring we attach the harness to the ball (which can be done with no expenditure of effort), so the ball and ring now oscillate with a much smaller amplitude and higher frequency, as illustrated below for the configuration of maximum extension. |
|
|
|
|
|
|
|
This oscillating configuration is quite distinct from the initial slow oscillation of the two objects interacting solely through their mutual gravitational attraction. With the springs attached, we might regard the overall configuration as a single object with an internal energy mode, i.e., we might say the final state is a single object with an elevated temperature, since the original potential-kinetic energy has been converted into the small rapid oscillation of the combined masses. This is conceptually similar to the example of two lumps of inelastic clay, which collide to form a single lump with elevated temperature, because the internal vibrational modes of the clay have absorbed the kinetic energy of the collision. Superficially the linking of the ball and ring by means of the spring harness might appear to be an irreversible action… and yet we can, at any time when the ball and ring coincide at x = 0, disconnect the relaxed spring harness, and return the system to its original gravitationally bound oscillation. In other words, it is quite easy to recover the initial state with no expenditure of effort. Admittedly the restoration of the initial state requires the spring harness to be released at a precise point in the cycle, so if it is released at random there is zero probability of re-attaining the original state, so in this sense the attachment of the springs has removed the system from immediate contact with its initial state. Nevertheless we can easily conceive of the springs being released at the point of alignment, so we may be inclined to regard this process as reversible, and therefore to think the entropy of the system has not changed. |
|
|
|
The reason it is so easy to recover the initial state in this example is that the energy of the system has not lost any coherence. All the particles of the ball still move together in unison, as do all the particles of the ring. In fact, it’s worth noting that the spring cycle and the gravitational cycle share a common point in phase space, namely, the point when the ball and ring are aligned and all the energy of the system is kinetic. Naturally this is the point at which we can shift from one cycle to the other with no expenditure of effort. |
|
|
|
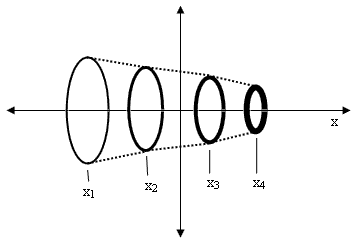
But now suppose we have an arrangement of N rings (of equal mass) whose axes are all aligned with the x axis, and suppose three of the rings are initially rigidly attached to each other, and the fourth is positioned so the center of mass is at x = 0, as illustrated below. |
|
|
|
|
|
|
|
As with the ball and ring, the two elements of this system will undergo a simple oscillation under the influence of their mutual gravitational attraction. Of course, the amplitude of the single ring will be three times the amplitude of the three rigidly connected rings, so the center of mass remains constantly at x = 0. As before, we can imagine that the single ring has a harness of springs that can be attached to the largest of the three other springs with no expenditure of effort when all the rings are aligned at x = 0, and this will lead to an oscillating system with much smaller amplitude and higher frequency. Also, we can easily restore the original purely gravitational oscillation by disconnecting the springs at any alignment event. |
|
|
|
Now, to change the situation slightly, suppose each of the three clustered rings is linked to its nearest neighbors by springs (as well as being rigidly attached), and suppose at one of the alignment events when all four rings are at x = 0 we attach the outer-most ring and we release the rigid connections between the three clustered rings. In this condition we now have four rings of equal mass, each attached to its nearest neighbor(s) by springs, somewhat as illustrated in the exploded view below. |
|
|
|
|
|
|
|
The initial condition for this system is |
|
|
|
|
|
|
|
In the spring-bound oscillation the effects of gravity are negligible, and we can assume each spring exerts a force directly proportional to its extension, i.e., to the difference in position between neighboring rings. On this basis the equations of motion are |
|
|
|
|
|
|
|
Noting that x1 + x2 + x3 + x4 = 0, there are really just three independent equations, so we can define the differences ξj = xj+1 – xj and write the system equations as |
|
|
|
|
|
|
|
The characteristic polynomial is |
|
|
|
|
|
|
|
with the roots |
|
|
|
|
|
|
|
It follows that the general solution is of the form |
|
|
|
|
|
|
|
Where |
|
|
|
|
|
We also stipulate that ξj(0) = 0 for all j, and we are given the initial differences in velocity for each neighboring pair of rings, so we can use this information together with the basic equations of motion to generate a table of initial conditions: |
|
|
|
|
|
|
|
The even-order derivatives are all zero, so the cosine terms in the expressions for the xj are zero. The coefficients of the sine terms can be found by differentiating the general solution to give the first, third, and fifth derivatives, and setting them equal to the expressions from the above table of initial conditions. Writing the jth solution as |
|
|
|
|
|
|
|
we get the system of equations |
|
|
|
|
|
|
|
Hence we have |
|
|
|
|
|
|
|
where the symbol |
|
|
|
|
|
|
|
In our example we have the initial conditions |
|
|
|
|
|
|
|
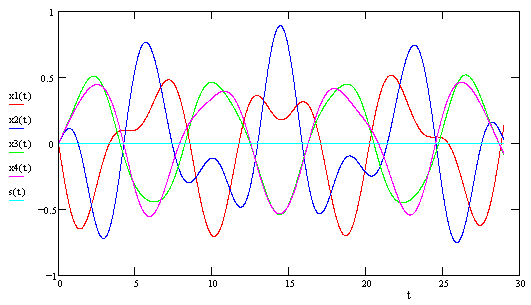
The positions of the four rings as functions of time are shown in the plot below. |
|
|
|
|
|
|
|
As in the previous cases, the total energy is conserved, merely having been converted to small and rapid oscillatory motions. However, in this case there is an obvious loss of coherence. Each of the four masses follows a unique “orbit”, and the periods of these orbits are not rational multiples of each other. Therefore, there is no instant (after t = 0) at which we could, without the expenditure of effort, cause the system to recur to its original state. (Note that “free” changes in the configuration effected by attachment or disconnection of ideal massless springs between two entities must occur only when the entities are coincident to avoid non-ideal losses due to snapping or stretching of the spring, and similarly ideal rigid connections must be made and broken only when the entities are matched in speed to avoid non-ideal losses due to impact.) As a result, we consider the transition from the initial gravity-dominated cycle to this spring-dominated cycle to be irreversible. |
|
|
|
These examples illustrate several different ways in which the state of a system may evolve. In the first case, with sphere and torus, the system began with gravitational potential energy but no kinetic energy, and then the components underwent gravitational contraction, converting potential to kinetic energy, but coherence was maintained, and the system followed a simple cyclical path through phase space. Then we introduced a different energy mode, but again coherence was maintained, so the system followed one of two simple cyclical paths through phase space, and could effortlessly be switched from one path to the other at the points of intersection. Then we introduced multiple internal energy modes for the main components, and found that coherence was immediately lost, so it was no longer possible to effortlessly restore the original cycle. The transition from coherent to incoherent energy modes characterizes the conversion of kinetic energy into “heat”. Incidentally, these examples also suggest the possibility of creating “pseudo-heat”, by putting energy into numerous energy modes that appear to be incoherent, but that actually maintain an underlying coherence which could be exploited to restore the initial state. |
|
|
|
However, the above discussion makes use of idealized classical entities, such as the massless ideal springs. We considered the microscopic forces of attraction between particles that enable them to have vibrational modes that absorb as “heat” the kinetic energy produced by the gravitational collapse, but we represented these microscopic (inter-molecular) forces of attraction as ideal springs, so energy was conserved within the system. This is perfectly legitimate from a classical mechanical perspective, but (like classical physics in general) it ultimately leads to an “ultraviolet catastrophe”. Ideal springs are incompatible with the second law of thermodynamics. In order to correctly account for thermodynamic phenomena, it is necessary to take account of the fundamental nature of the oscillators on the smallest scale, which ultimately involve electromagnetic interactions and Coulomb exchanges between discrete charged particles. The oscillations are therefore necessarily accompanied by the emission of radiation, which will tend toward an equilibrium condition. All bodies have a radiant temperature, and this must be taken into account when determining the thermodynamic equilibrium of a system (such as a collapsing gas cloud) with its surrounding. To express this in easily visualized terms for our mechanistic discussion above, we must take account of the fact that compressing a spring causes the temperature of the material to rise. The molecular interactions unavoidably involve the emission (as well as absorption) of radiation. With the addition of enough compression energy, the springs would begin to glow red hot (and then white hot) as more and more energy is put into them. This represents radiant energy, elevating the entropy of the surroundings. This is a good illustration of how a general fundamental principle like the second law of thermodynamics can lead us to non-trivial conclusions about detailed physical processes – such as the physical impossibility of ideal springs. The second law requires us to explicitly account for the irreducible quantum processes at the molecular level, and the associated electromagnetic radiation, when evaluating gravitational collapse. |
|
|