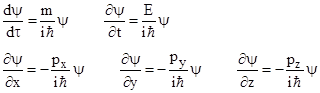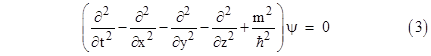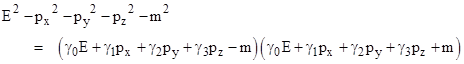Polarization and Spin

Every ray of light has therefore two opposite sides… And since the crystal by this disposition or virtue does not act upon the rays except when one of their sides of unusual refraction looks toward that coast, this argues a virtue or disposition in those sides of the rays which answers to and sympathizes with that virtue or disposition of the crystal, as the poles of two magnets answer to one another…

                                                                           Newton, 1717

A transparent crystalline substance, now known as calcite, was discovered by a naval expedition to Iceland in 1668, and samples of this “Iceland crystal” were examined by the Danish scientist Erasmus Bartholin, who noticed that a double image appeared when objects were viewed through this crystal. He found that rays of light passing through calcite are split into two refracted rays. Some of the incoming light is always refracted at the normal angle of refraction for the density of the substance and a given angle of incidence, but some of the incoming light is refracted at a different angle. If the incident ray is perpendicular to the face of the crystal, the ordinary ray undergoes no refraction and passes straight through, just as we would expect, but the extraordinary ray is refracted upon entering the crystal and again upon departing the crystal. Bartholin noted that the direction in which the extraordinary ray diverges from the perpendicular as it passes into the crystal depends on the orientation of the crystal about the incident axis. Thus by rotating the crystal about the incident axis, the second image appearing through the crystal revolves around the first image. This phenomenon could have been observed at any time in human history, and might not have been regarded as terribly significant, but by the middle of the 17th century the study of optics had reached a point where the occurrence of two distinct refracted rays was a clear anomaly. Bartholin called this “one of the greatest wonders that nature has produced”. (It’s interesting that Bartholin’s daughter, Anne Marie, married Ole Roemer, whose discovery of the finite speed of light was discussed in Section 3.3.)

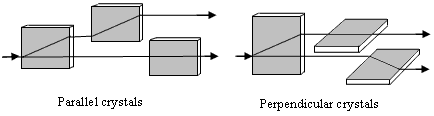
Christiaan Huygens had previously derived the ordinary law of refraction from his wave theory light by assuming that the speed of light in a refracting substance is the same in all directions, i.e., isotropic. When Huygens learned of the double refraction in the Iceland crystal (also known as Iceland spar) he concluded that the crystal must contain two different media interspersed, and that the speed of light is isotropic in one of these media but anisotropic in the other. Hence he imagined that two distinct wave fronts emanated from each point, one spherical and the other ellipsoidal, and the directions of the two rays were normal to these two wave fronts. He didn’t explain why part of the light propagated purely in one of the media, and part of the light purely in the other. Moreover, he discovered another very remarkable phenomena related to this double refraction that was even more difficult to reconcile with his implicitly longitudinal conception of light waves. He found that if a ray of light, after passing through an Iceland crystal, is passed through a second crystal aligned parallel with the first, then all of the ordinary ray passes through the second crystal without refraction, and all of the extraordinary ray is refracted in the second crystal just as it was in the first. On the other hand, if the secondary crystals are aligned perpendicular to the first, the refracted ray from the first crystal is not refracted at all in the second crystal, whereas the un-refracted ray from the first crystal undergoes refraction in the second. These two cases are depicted in the figures below.

Huygens was unable to account for this behavior in any way that was consistent with his conception of light as a longitudinal wave with radial symmetry. He conceded

…it seems that one is obliged to conclude that the waves of light, after having passed through the first crystal, acquire a certain form or disposition in virtue of which, when meeting the texture of the second crystal, in certain positions, they can move the two different kinds of matter which serve for the two species of refraction; and when meeting the second crystal in another position are able to move only one of these kinds of matter. But to tell how this occurs, I have hitherto found nothing which satisfies me.

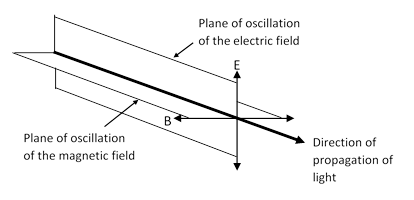
Newton considered this phenomena to be inexplicable “if light be nothing other than pression or motion through an aether”, and argued that “the unusual refraction is [due to] an original property of the rays”, namely, an axial asymmetry or sidedness, which he thought must be regarded as an intrinsic property of individual corpuscles of light. In the Opticks he wrote that “rays of light seem to be hard bodies, for otherwise they would not retain different properties in their different sides”. At the beginning of the 19th century the “sidedness” of Newton of reconciled with the wave concept of Huygens by the idea of light as a transverse (rather than longitudinal) wave. Later this transverse wave was found to be a feature of the electromagnetic waves predicted by Maxwell’s equations, according to which the electric and magnetic fields oscillate transversely in the plane normal to the direction of motion (and perpendicular to each other). Thus an electromagnetic wave "looks" something like this:

where E signifies the oscillating electric field and B the magnetic field. The wave is said to be polarized in the direction of E. The osculating planes are perpendicular to each other, but their orientations are not necessarily fixed − it's possible for them to rotate like a windmill about the axis of propagation. In general the electric field of a plane wave of frequency ω propagating along the z axis of Cartesian coordinates can be resolved into two perpendicular components that can be written as

where ϕ is the phase difference between the two components, and C_x and C_y are the constant amplitudes. If the amplitudes of these two components both equal a single constant E₀, and if the phase difference is –π/2, then remembering the trigonometric identity sin(u) = cos(u – π/2), we have

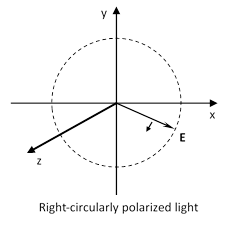
In this case the amplitude of the overall wave is constant, and, as can be seen in the figure below, the electric field vector at constant z rotates (at the angular speed ω) in the clockwise direction as seen by an observer looking back toward the approaching wave.

This is conventionally called right-circularly polarized light. On the other hand, if the amplitudes are equal but the phase difference is +π/2, then remembering the trigonometric identity sin(u) = –cos(u + p/2), the two components are

so the direction of the electric field rotates in the counter-clockwise direction. This is called left-circularly polarized light. If we superimpose left and right circularly polarized waves (with the same frequency and phase), The result is simply

which represents a linearly polarized wave, since the electric field oscillates entirely in the xz plane. By combining left and right circularly polarized light in other proportions and with other phase relations, we can also produce what are called elliptically polarized light waves, which are intermediate between the extremes of circularly polarized and linearly polarized light. Conversely, a circularly polarized light wave can be produced by combining two perpendicular linearly polarized waves.

A typical plane wave of ordinary light (such as from the Sun) consists of components with all possible polarizations mixed together, but it can be decomposed into left and right circularly polarized waves, and this can be done relative to any orthogonal set of axes. Calcite crystals (as well as some other substances) have an isotropic index of refraction for light whose electric field oscillates in one particular plane, but an anisotropic index of refraction for light whose electric field oscillates in the perpendicular plane. Hence it acts as a filter, decomposing the incident wave (normal to the surface) into perpendicular linearly polarized waves aligned with the characteristic axis of the crystal. As the wave enters the crystal, only the component whose electric plane of oscillation encounters anisotropic refractivity is subjected to refraction. This is the classical account of the phenomena observed by Bartholin and Huygens.

It could be argued that the classical account of polarization phenomena is incomplete, because it relies on the assumption that a superposition of plane waves can be decomposed into an arbitrary set of orthogonal components, and that the interactions of those components with matter will yield the same results, regardless of the chosen basis of decomposition. The difficulty can be seen by considering how a polarizing crystal can prevent exactly half of the waves from passing through while allowing the other half to pass through. The incident beam consists of waves whose polarization axes are distributed uniformly in all direction, so one might expect to find that only a very small fraction of the waves would pass through a perfect polarizing substance. In fact, the fraction of waves from a uniform distribution with polarizations exactly aligned with the polarizing axis of a substance should be vanishingly small. Likewise it isn’t easy to explain, from the standpoint of classical electrodynamics, why half of the incident wave energy is diverted in one discrete direction, rather than being distributed over a range of refraction angles. The process seems to be discretely binary, i.e., each bit of incident energy must go in one of just two directions, even though the polarization angles of the incident energy are uniformly distributed over all directions. The precise mechanism for how this comes about requires a detailed understanding of the interactions between matter and electromagnetic radiation – something which classical electrodynamics was never able to provide.

If we discard the extraordinary ray emerging from a calcite polarizing prism, the crystal functions as a filter, producing a beam of a linearly polarized light. The thickness of a polarizing filter isn't crucial (assuming the polarization axis is perfectly uniform throughout the substance), because the first surface effectively "selects" the suitably aligned waves, which then pass freely through the rest of the substance. The light emerging from the other side is plane-polarized with half the intensity of the incident light. Now, as noted above, if we pass this polarized beam through another polarizing filter oriented parallel to the first, then all the energy of the incident polarized beam will be passed through the second filter. On the other hand, if the second filter is oriented perpendicular to the first, none of the polarized beam’s energy will get through the second filter. For intermediate angles, Etienne Malus (a captain in the army of Napoleon Bonaparte) discovered in 1809 that the intensity of the beam emerging from the second polarizing filter is I cos(θ)², where I is the intensity of the beam emerging from the first filter and θ is the angle between the two filters.

Incidentally, it’s possible to convert circularly polarized incident light into plane-polarized light of the same intensity. The traditional method is to use a "quarter-wave plate" thickness of a crystal substance such as mica. In this case we're not masking the non-aligned components, but rather introducing a relative phase shift between them so as to force them into alignment. Of course, a particular thickness of plate only "works" this way for a particular frequency.

In 1922 the Dutch physicists Otto Stern and Walther Gerlach made a discovery remarkably similar to that of Erasmus Bartholin, but instead of light rays their discovery involved the trajectories of elementary particles of matter. They passed a beam of particles (atoms of silver) through an oriented magnetic field, and found that the beam split into two beams, with about half the particles in each beam, one deflected up (relative to the direction of the magnetic field) and the other down. This is depicted in the figure below.

Ultimately this behavior was recognized as being a consequence of the intrinsic spin of elementary particles. The idea of intrinsic spin was introduced by Uhlenbeck and Goudsmit in 1925, and was soon incorporated (albeit in a somewhat ad hoc way) into the formalism of quantum mechanics by postulating that the wave function of a particle can be decomposed into two components, which we might label ψ_UP and ψ_DOWN, relative to any given orientation of the magnetic field. These components are weighted and the sum of the squares of the weights equals 1. (The overall state-vector for the particle can be expressed as the Cartesian product of a non-spin vector times the spin vector.) The observable "spin" then corresponds to three operators that are proportional to the Pauli spin matrices:

These operators satisfy the commutation relations

as we would expect by the correspondence principle from ordinary (classical) angular momentum. Not surprisingly, this non-commutation is closely related to the non-commutation of ordinary spatial rotations of a classical particle, in the sense that they're both related to the cross-product of orthogonal vectors. Given an orthogonal coordinate system [x,y,z] the angular momentum of a classical particle with momentum [p_x, p_y, p_z] is (in component form)

Guided by the correspondence principle, we replace the classical components p_x, p_y, p_z with their quantum mechanical equivalents, the differential operators

leading to the S operators noted above. Although this works, it is not entirely satisfactory, first because it is ad hoc, and second because it is not relativistic. Both of these shortcomings were eliminated by Dirac in 1928 when he developed the first relativistic equation for an elementary massive particle. The Dirac equation is one of the greatest examples of the heuristic power of the principle of relativity, leading not only to an understanding of the necessity of intrinsic spin, but also to the prediction of anti-matter, and ultimately to quantum field theory. Recall from Section 2.3 that the invariant spacetime interval along the path of a timelike particle of mass m in special relativity is

and if we multiply through by m²/(dt)² and make the identifications E = m(dt/dτ), p_x = m(dx/dτ), etc., this gives

Also, if we postulate that the particle is described by a wave function ψ(t,x,y,z) we can differentiate with respect to τ to give

multiplying through by m and making the identifications for E, p_x, p_y, p_z, we get

This relation would be equivalent to equation (1) if we put

where  is a constant. This suggests the operator correspondences

on the basis of which equation (2) can be re-written as

which, if we identify  with the reduced Planck constant h/(2π), is the Klein-Gordon wave equation. Unfortunately the solutions of this equation do not give positive-definite probabilities, so it was ruled out as a possible quantum mechanical wave function for a massive particle. Schrödinger’s provisional alternative was to base his wave mechanics on the non-relativistic version of equation (1), which is simply E = p²/(2m). This led to the familiar Schrödinger equation, whose solutions do give positive-definite probabilities, and which was highly successful in non-relativistic contexts. Still, Dirac was dissatisfied, and sought a relativistic wave equation with positive-definite probabilities. Dirac’s solution was to factor the quadratic equation (1) into linear factors, and take one of those factors as the basis of the quantum mechanical wave equation. Of course, equation (1) doesn’t factor if we restrict ourselves to the set of real numbers, but it can be factored in different classes of mathematical entities, just as x²+1 can’t be factored if we are restricted to real numbers, but it factors as (x+i)(x–i) if we allow imaginary as well as real units.

In order to factor equation (1), Dirac postulated a set of basis variables γ₀, γ₁, γ₂, and γ₃ (not necessarily commuting) such that

Expanding the product and collecting terms, we find that this is a valid equality if and only if the four variables γ_j satisfy the relations

for all i,j = 0,1,2,3 with i ≠ j. These four quantities, along with unity, form the basis of what is called a Clifford algebra. The natural representation of these “quantities” is as 4x4 matrices. Equation (1) is solved provided either of the factors equals zero. Setting the first factor equal to zero and making the operator substitutions for energy and momentum, we arrive at Dirac’s equation

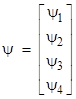
Since the operator is four-dimensional, the wave function must be a vector with four components, i.e., we have

The four components encode the different possible intrinsic spin states of the particle, subsuming the earlier ad hoc two-dimensional state vector. The appearance of four components instead of just two is due to the fact that these state vectors also encompass negative energy states as well as positive energy states. This was inevitable, considering that the relativistic equation (1) is satisfied equally well by –E as well as +E.

It may be surprising at first that equation (4), which is linear, is nevertheless covariant under Lorentz transformations. The covariance certainly isn’t obvious, and it is achieved only by stipulating that the components of ψ transform not as an ordinary four-vector, but as two spinors. Thus the requirement for Lorentz covariance leads directly to the existence of intrinsic spin for any massive particle described by Dirac’s equation, including electrons. (Such particles are said to possess “spin 1/2”, since it can be shown that the angular momentum represented by their intrinsic spin is .) In addition, when the interaction with an electromagnetic field is included in the Dirac equation, the requirement for Lorentz covariance leads to the existence of anti-particles. The positron, which is the anti-particle of the electron, was predicted by Dirac around 1929, and found experimentally just two years later. Fundamentally, the Dirac equation introduced, for the first time, the idea that any relativistic treatment of one particle must inevitably involve consideration of other particles, and from this emerged the concept of second quantization and quantum field theory. In effect, quantum field theory requires us to consider not just the field of a single identified particle, but the field of all such fields. (It’s interesting to compare this with the view of the metric of spacetime as the “field of all fields” discussed in Section 4.6.)

One outcome of quantum field theory was a quantization of the electromagnetic field, the necessity of which had been pointed out by Einstein as early as 1905. On an elementary level, Maxwell’s equations are inadequate to describe the phenomena of radiation. The quantum of electromagnetic radiation is called the photon, which behaves in some ways like an elementary particle, although it is massless, and therefore always propagates at the speed of light. Hence the "spin axis" of a photon is always parallel to its direction of motion, pointing either forward or backward, as illustrated below.

These two states correspond to left-handed and right-handed photons. Whenever a photon is absorbed by an object, an angular momentum of either  or  is imparted to the object. Each photon is characterized not only by its energy (frequency) and its phase, but also by it’s propensity to exhibit each of the two possible states of spin when it interacts with an object. A beam of light, consisting of a large number of photons, is characterized by the energies, phase relations, and spin propensities of its constituent photons. This could be said to vindicate Newton’s belief that rays of light posses a previously unknown “original property” that affects how they are refracted. Recall that, in classical electromagnetic theory, the plane of oscillation of the electric field of circularly polarized light rotates about the axis of propagation (in one direction or the other). When such light impinges on a surface, it imparts angular momentum due to the rotation of the electric field. In quantum theory this corresponds to a stream of photons with a high propensity for being right-handed (or for being left-handed), so that each photon contributes to the overall angular momentum imparted to the absorbing object.

On the other hand, linearly polarized light (in classical electrodynamics) does not impart any angular momentum to the absorbing object. This is represented in quantum theory by a stream of photons, each with equal propensity to exhibit right-handed or left-handed spin. Each individual interaction, i.e., each absorption of a photon, imparts either  or  to the absorbing object, so if the intensity of a linearly polarized beam of light is lowered to the point that only one photon is transmitted at a time, it will appear to be circularly polarized (either left or right) for each photon, which of course is not predicted by classical theory. (In a sense, Maxwell’s equations can be regarded as a crude form of the Schrödinger equation for light, but it obviously does not represent all the quantum mechanical effects.) However, for a large stream of such photons, the net angular momentum is essentially zero, because half of the photons interact in the right-handed sense and half in the left-handed sense. This corresponds (loosely) to the fact in classical theory that linearly polarized light can be regarded as a superposition of left and right circularly polarized light.

Incidentally, most people have personal "hands on" knowledge of polarized electromagnetic waves without even realizing it. The waves broadcast by a radio or television tower are naturally polarized, and if you've ever adjusted the orientation of "rabbit ears" and found that your reception is better at some orientations than at others, for a particular station, you've demonstrated the effects of electromagnetic wave polarization.

The behavior of intrinsic spin of elementary particles can be used to illustrate some important features of quantum mechanics – features which Einstein famously referred to as “spooky action at a distance”. This behavior is discussed in the next section.

Return to Table of Contents