9.1  In the Neighborhood

 

Nothing puzzles me more than time and space; and yet nothing troubles me less, as I never think about them.

                                       Charles Lamb (1775-1834)

 

It's customary to treat the relativistic spacetime manifold as an ordinary topological space with the same topology as a four-dimensional Euclidean manifold, denoted by R4.  This is typically justified by noting that the points of spacetime can be parameterized by a set of four coordinates x,y,z,t, and defining the "neighborhood" of a point somewhat informally as follows (quoted from Ohanian and Ruffinni):

 

...the neighborhood of a given point is the set of all points such that their coordinates differ only a little from those of the given point.

 

Of course, the neighborhoods given by this definition are not Lorentz-invariant, because the amount by which the coordinates of two points differ is highly dependent on the frame of reference.  Consider, for example, two spacetime points in the xt plane with the coordinates {0,0} and {1,1} with respect to a particular system of inertial coordinates.  If we consider these same two points with respect to the frame of an observer moving in the positive x direction with speed v (and such that the origin coincides with the former coordinate origin), the differences in both the space and time coordinates are reduced by a factor of , which can range anywhere between 0 and ∞.  Thus there exist valid inertial reference systems with respect to which both of the coordinates of these points differ (simultaneously) by as little or as much as we choose.  Based on the above definition of neighborhood (i.e., points whose coordinates “differ only a little”), how can we decide if these two points are in the same neighborhood?

 

It might be argued that the same objection could be raised against this coordinate-based definition of neighborhoods in Euclidean space, since we're free to scale our coordinates arbitrarily, which implies that the numerical amount by which the coordinates of two given (distinct) points differ is arbitrary.  However, in Euclidean space this objection is unimportant, because we will arrive at the same definition of limit points, and thus the same topology, regardless of what scale factor we choose.  In fact, the same applies even if we choose unequal scale factors in different directions, provided those scale factors are all finite and non-zero. 

 

From a strictly mathematical standpoint, the usual way of expressing the arbitrariness of metrical scale factors for defining a topology on a set of points is to say that if two systems of coordinates are related by a diffeomorphism (a differentiable mapping that possess a differentiable inverse), then the definition of neighborhoods in terms of "coordinates that differ only a little" will yield the same limit points and thus the same topology.  However, from the standpoint of a physical theory it's legitimate to ask whether the set of distinct points (i.e., labels) under our chosen coordinate system actually corresponds one-to-one with the distinct physical entities whose connectivities we are tying to infer.  For example, we can represent formal fractions x/y for real values of x and y as points on a Euclidean plane with coordinates (x,y), and conclude that the topology of formal fractions is R2, but of course the value of every fraction lying along a single line through the origin is the same, and the values of fractions have the natural topology of R1 (because the reals are closed under division, aside from divisions by zero). If the meanings assigned to our labels are arbitrary, then these are simply two different manifolds with their own topologies, but for a physical theory we may wish to decide whether the true objects of our study - the objects with ontological status in our theory - are formal fractions or the values of fractions.  When trying to infer the natural physical topology of the points of spacetime induced by the Minkowski metric we face a similar problem of identifying the actual physical entities whose mutual connectivities we are trying to infer, and the problem is complicated by the fact that the "Minkowski metric" is not really a metric at all (as explained below).

 

Recall that for many years after general relativity was first proposed by Einstein there was widespread confusion and misunderstanding among leading scientists (including Einstein himself) regarding various kinds of singularities. The main source of confusion was the failure to clearly distinguish between singularities of coordinate systems as opposed to actual singularities of the manifold/field. This illustrates how we can be misled by the belief that the local topology of a physical manifold corresponds to the local topology of any particular system of coordinates that we may assign to that physical manifold. It’s entirely possible for the “manifold of coordinates” to have a different topology than the physical manifold to which those coordinates are applied. With this in mind, it’s worthwhile to consider carefully whether the most physically meaningful local topology of spacetime is necessarily the same as the topology of the usual four-dimensional systems of coordinates that are conventionally applied to it.

 

Before examining the possible topologies of Minkowski spacetime in detail, it's worthwhile to begin with a review of the basic definitions of point set topologies and topological spaces.  Given a set S, let P(S) denote the set of all subsets of S.  A topology for the set S is a mapping T from the Cartesian product {S ´ P(S)} to the discrete set {0,1}.  In other words, given any element e of S, and any subset A of S, the mapping T(A,e) returns either 0 or 1.  In the usual language of topology, we say that e is a limit point of A if and only if T(A,e) = 1.

 

As an example, we can define a topology on the set of points of 2D Euclidean space equipped with the usual Pythagorean metric

 

 

by saying that the point e is a limit point of any subset A of points of the plane if and only if for every positive real number ε there is an element u (other than e) of A such that d(e,u) < ε.  Clearly this definition relies on prior knowledge of the "topology" of the real numbers, which is denoted by R1.  The topology of 2D Euclidean space is called R2, since it is just the Cartesian product R1 x R1. 

 

The topology of a Euclidean space described above is actually a very special kind of topology, called a topological space.  The distinguishing characteristic of a topological space S,T is that S contains a collection of subsets, called the open sets (including S itself and the empty set) which is closed under unions and finite intersections, and such that a point p is a limit point of a subset A of S if and only if every open set containing p also contains a point of A distinct from p.  For example, if we define the collection of open spherical regions in Euclidean space, together with any regions that can be formed by the union or finite intersection of such spherical regions, as our open sets, then we arrive at the same definition of limit points as given previously.  Therefore, the topology we've described for the points of Euclidean space constitutes a topological space.  However, it's important to realize that not every topology is a topological space.

 

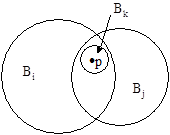
The basic sets that we used to generate the Euclidean topology were spherical regions defined in terms of the usual Pythagorean metric, but the same topology would also be generated by any other metric.  In general, a basis for a topological space on the set S is a collection B of subsets of S whose union comprises all of S and such that if p is in the intersection of two elements Bi and Bj of B, then there is another element Bk of B which contains p and which is entirely contained in the intersection of Bi and Bj, as illustrated below for circular regions on a plane.

 

 

Given a basis B on the set S, the unions of elements of B satisfy the conditions for open sets, and hence serve to define a topological space.  (This relies on the fact that we can represent non-circular regions, such as the intersection of two circular open sets, as the union of an infinite number of circular regions of arbitrary sizes.)

 

If we were to substitute the metric

 

d(a,b)  =  |xa − xb|  +  |ya − yb|

 

in place of the Pythagorean metric, then the basis sets, defined as loci of points whose "distances" from a fixed point p are less than some specified real number r, would be square-shaped diamonds instead of circles, but we would arrive at the same topology, i.e., the same definition of limit points for the subsets of the Euclidean plane E2.  In general, any true metric will induce this same local topology on a manifold.  Recall that a metric is defined as a distance function d(a,b) for any two points a,b in the space satisfying the three axioms

 

                        (1)  d(a,b) = 0   if and only if a = b

                        (2)  d(a,b) = d(b,a)   for each a,b

                        (3)  d(a,c) ≤ d(a,b) + d(b,c)   for all a,b,c

 

It follows that d(a,b) ≥ 0 for all a,b.  Any distance function that satisfies the conditions of a metric will induce the same (local) topology on a set of points, and this will be a topological space.

 

However, it's possible to conceive of more general "distance functions" that do not satisfy all the axioms of a metric.  For example, we can define a distance function that is commutative (axiom 2) and satisfies the triangle inequality (axiom 3), but that allows d(a,b) = 0 for distinct points a,b.  Thus we replace axiom (1) with the weaker requirement d(a,a) = 0.  Such a distance function is called a pseudometric.  Obviously if a,b are any two points with d(a,b) = 0 we must have d(a,c) = d(b,c) for every point c, because otherwise the points a,b,c would violate the triangle inequality.  Thus a pseudometric partitions the points of the set into equivalence classes, and the distance relations between these equivalence classes must be metrical.  We've already seen a situation in which a pseudometric arises naturally, if we define the distance between two points in the plane of formal fractions as the absolute value of the difference in slopes of the lines from the origin to those two points.  The distance between any two points on a single line through the origin is therefore zero, and these lines represent the equivalence classes induced by the pseudometric.  Of course, the distances between the slopes satisfy the requirements of a metric.  Therefore, the absolute difference of value is a pseudometric for the space of formal fractions. 

 

Now, we know that the points of a two-dimensional plane can be assigned the R2 topology, and the values of fractions can be assigned the R1 topology, but what kind of local topology is induced on the two-dimensional space of formal fractions by the pseudometric?  We can use our pseudometric distance function to define a basis, just as with a metrical distance function, and arrive at a topological space, but this space will not generally possess all the separation properties that we commonly expect for distinct points of a topological space. 

 

It's convenient to classify the separation properties of topological spaces according to the "trennungsaxioms", also called the Ti axioms, introduced by Alexandroff and Hopf.  These represent a sequence of progressively stronger separation axioms to be met by the points of a topological space.  A space is said to be T0 if for any two distinct points at least one of them is in a neighborhood that does not include the other.  If each point is contained in a neighborhood that does not include the other, then the space is called T1.  If the space satisfies the even stronger condition that any two points are contained in disjoint open sets, then the space is called T2, also known as a Hausdorff space.  There are still more stringent separation axioms that can be applied, corresponding to T3 (regular), T4 (normal), and so on.

 

Many topologists will not even consider a topological space which is not at least T2 (and some aren't interested in anything which is not at least T4), and yet it's clear that the topology of the space of formal fractions induced by the pseudometric of absolute values is not even T0, because two distinct fractions with the same value (such as 1/3 and 2/6) cannot be separated into different neighborhoods by the pseudometric.  Nevertheless, we can still define the limit points of the set of formal fractions based on the pseudometric distance function, thereby establishing a perfectly valid topology.  This just illustrates that the distinct points of a topology need not exhibit all the separation properties that we usually associate with distinct points of a Hausdorff spaces (for example).

 

Now let's consider 1+1 dimensional Minkowski spacetime, which is physically characterized by an invariant spacetime interval whose magnitude is

 

 

Empirically this appears to be the correct measure of absolute separation between the points of spacetime, i.e., it corresponds to what clocks measure along timelike intervals and what rulers measure along spacelike intervals.  However, this distance function clearly does not satisfy the definition of a metric, because it can equal zero for distinct points.  Moreover, it is not even a pseudo-metric, because the interval between points a and b is always greater than the sum of the intervals from a to c and from c to b, contradicting the triangle inequality.  For example, it's quite possible in Minkowski spacetime to have two sides of a "triangle" equal to zero while the remaining side is billions of light years in length.  Thus, the absolute interval of space-time does not provide a metrical measure of distance in the strict sense.  Nevertheless, in other ways the magnitude of the interval d(a,b) is quite analogous to a metrical distance, so it's customary to refer to it loosely as a "metric", even though it is neither a true metric nor even a pseudometric.  We emphasize this fact to remind ourselves not to prejudge the topology induced by this distance function on the points of Minkowski spacetime, and not to assume that distinct events possess the separation properties or connectivities of a topological space.

 

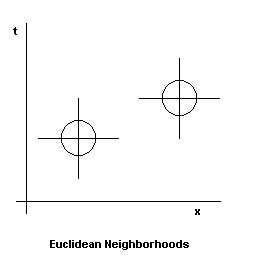
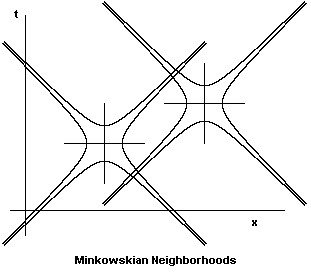
The ε-neighborhood of a point p in the Euclidean plane based on the Pythagorean metric (1) consists of the points q such that d(p,q) < ε.   Thus the ε-neighborhoods of two points in the plane are circular regions centered on the respective points, as shown in the left-hand illustration below.  In contrast, the ε-neighborhoods of two points in Minkowski spacetime induced by the Lorentz-invariant distance function (2) are the regions bounded by the hyperbolic envelope containing the light lines emanating from those points, as shown in the right-hand illustration below.

 

This illustrates the important fact that the concept of "nearness" implied by the Minkowski metric is non-transitive.  In a metric (or even a pseudometric) space, the triangle inequality ensures that if A and B are close together, and B and C are close together, then A and C cannot be very far apart.  This transitivity obviously doesn't apply to the absolute magnitudes of the spacetime intervals between events, because it's possible for A and B to be null-separated, and for B and C to be null separated, while A and C are arbitrarily far apart.

 

Interestingly, it is often suggested that the usual Euclidean topology of spacetime might break down on some sufficiently small scale, such as over distances on the order of the Planck length of roughly 10−35 meters, but the system of reference for evaluating that scale is usually not specified.  As noted previously, the spatial and temporal components of two null-separated events can both simultaneously be regarded as arbitrarily large or arbitrarily small (including less than 10−35 meters), depending on which system of inertial coordinates we choose.  This null-separation condition permeates the whole of spacetime (recall Section 1.10 on Null Coordinates), so if we take seriously the possibility of non-Euclidean topology on the Planck scale, we can hardly avoid considering the possibility that the effective physical topology ("connectedness") of the points of spacetime may be non-Euclidean along null intervals in their entirety, which span all scales of spacetime.

 

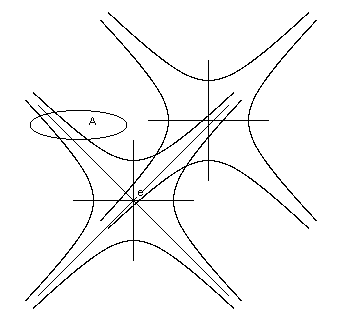
It's certainly true that the topology induced by a direct application of the Minkowski distance function (2) is not even a topological space, let alone Euclidean.  To generate this topology, we simply say that  the point e is a limit point of any subset A of points of Minkowski spacetime if and only if for every positive real number ε there is an element u (other than e) of A such that d(e,u) < ε.   This is a perfectly valid topology, and arguably the one most consistent with the non-transitive absolute intervals that seem to physically characterize spacetime, but it is not a topological space.  To see this, recall that in order for a topology to be a topological space it must be possible to express the limit point mapping in terms of open sets such that a point e is a limit point of a subset A of S if and only if every open set containing e also contains a point of A distinct from e.  If we define our topological neighborhoods in terms of the Minkowski absolute intervals, our open sets would naturally include complete Minkowski neighborhoods, but these regions don't satisfy the condition for a topological space, as illustrated below, where e is a limit point of A, but e is also contained in Minkowski neighborhoods containing no point of A.

 

The idea of a truly Minkowskian topology seems unsatisfactory to many people, because they worry that it implies every two events are mutually "co-local" (i.e., their local neighborhoods intersect), and so the entire concept of "locality" becomes meaningless.  However, the fact that a set of points possesses a non-positive-definite line element does not imply that the set degenerates into a featureless point  (which is fortunate, considering that the spacetime we inhabit is characterized by just such a line element).  It simply implies that we need to apply a more subtle understanding of the concept of locality, taking account of its non-transitive aspect.  In fact, the overlapping of topological neighborhoods in spacetime suggests a very plausible approach to explaining the "non-local" quantum correlations that seem so mysterious when viewed from the viewpoint of Euclidean topology.   We'll consider this in more detail in subsequent chapters.

 

It is, of course, possible to assign the Euclidean topology to Minkowski spacetime, but only by ignoring the non-transitive null structure implied by the Lorentz-invariant distance function.  To do this, we can simply take as our basis sets all the finite intersections of Minkowski neighborhoods.  Since the contents of an ε-neighborhood of a given point are invariant under Lorentz transformations, it follows that the contents of the intersection of the ε-neighborhoods of two given points are also invariant.  Thus we can define each basis set by specifying a finite collection of events with a specific value of ε for each one, and the resulting set of points is invariant under Lorentz transformations.  This is a more satisfactory approach than defining neighborhoods as the set of points whose coordinates (with respect to some arbitrary system of coordinates) differ only a little, but the fact remains that by adopting this approach we are still tacitly abandoning the Lorentz-invariant sense of nearness and connectedness, because we are segregating null-separated events into disjoint open sets.  This is analogous to saying, for the plane of formal fractions, that 4/6 is not a limit point of every set containing 2/3, which is certainly true on the formal level, but it ignores the natural topology possessed by the values of fractions.  In formulating a physical theory of fractions we would need to decide at some point whether the observable physical phenomena actually correspond to pairings of numerators and denominators, or to the values of fractions, and then select the appropriate topology.  In the case of a spacetime theory, we need to consider whether the temporal and spatial components of intervals have absolute significance, or whether it is only the absolute intervals themselves that are significant.

 

It's worth reviewing why we ever developed the Euclidean notion of locality in the first place, and why it's so deeply engrained in our thought processes, when the spacetime which we inhabit actually possesses a Minkowskian structure.  This is easily attributed to the fact that our conscious experience is almost exclusively focused on the behavior of macro-objects whose overall world-lines are nearly parallel relative to the characteristic of the metric.  In other words, we're used to dealing with objects whose mutual velocities are small relative to c, and for such objects the structure of spacetime does approach very near to being Euclidean.  On the scales of space and time relevant to macro human experience the trajectories of incoming and outgoing light rays through any given point are virtually indistinguishable, so it isn't surprising that our intuition reflects a Euclidean topology.  (Compare this with the discussion of Postulates and Principles in Chapter 3.1.)

 

Another important consequence of the non-positive-definite character of Minkowski spacetime concerns the qualitative nature of geodesic paths.  In a genuine metric space the geodesics are typically the shortest paths from place to place, but in Minkowski spacetime the timelike geodesics are the longest paths, in terms of the absolute value of the invariant intervals.  Of course, if we allow curvature, there may be multiple distinct "maximal" paths between two given events.  For example, if we shoot a rocket straight up (with less than escape velocity), and it passes an orbiting satellite on the way up, and passes the same satellite again on the way back down, then each of them has followed a geodesic path between their meetings, but they have followed very different paths.

 

From one perspective, it's not surprising that the longest paths in spacetime correspond to physically interesting phenomena, because the shortest path between any two points in Minkowski spacetime is identically zero.  Hence the structure of events was bound to involve the longest paths.  However, it seems rash to conclude that the shortest paths play no significant role in physical phenomena.  The shortest absolute timelike path between two events follows a "dog leg" path, staying as close as possible to the null cones emanating from the two events.  Every two points in spacetime are connected by a contiguous set of lightlike intervals whose absolute magnitudes are zero.

 

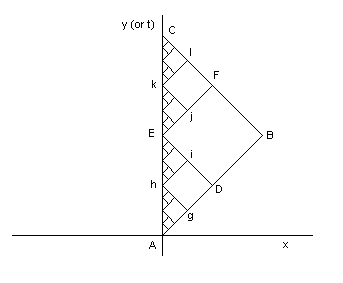
Minkowski spacetime provides an opportunity to reconsider the famous "limit paradox" from freshman calculus in a new context.  Recall the standard paradox begins with a two-part path in the xy plane from point A to point C by way of point B as shown below:

If the real segment AC has length 1, then the dog-leg path ABC has length , as does each of the zig-zag paths ADEFC, AghiEjklC, and so on.  As we continue to subdivide the path into more and smaller zigzags the envelope of the path converges on the straight line from A to C.  The "paradox" is that the limiting zigzag path still has length , whereas the line to which it converges (and from which we might suppose it is indistin­guishable) has length 1.  Needless to say, this is not a true paradox, because the limit of a set of convergents does not necessarily possess all the properties of the convergents.  However, from a physical standpoint it teaches a valuable lesson, which is that we can't necessarily assess the length of a path by assuming it equals the length of some curve from which it never differs by any measurable amount.

 

To place this in the context of Minkowski spacetime, we can simply replace the y axis with the time axis, and replace the Euclidean metric with the Minkowski pseudo-metric. We can still assume the length of the interval AC is 1, but now each of the diagonal segments is a null interval, so the total path length along any of the zigzag paths is identically zero.  In the limit, with an infinite number of infinitely small zigzags, the jagged "null path" is everywhere practically coincident with the timelike geodesic path AC, and yet its total length remains zero.  Of course, the oscillating acceleration required to propel a massive particle on a path approaching these light-like segments would be enormous, as would the frequency of oscillation.

 

Return to Table of Contents