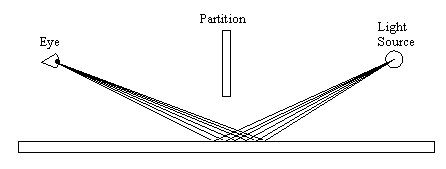8.11 Paths Not Taken |
|
|
|
Two roads diverged in a yellow wood, |
|
And sorry I could not travel both |
|
And be one traveler, long I stood |
|
And looked down one as far as I could |
|
To where it bent in the undergrowth… |
|
Robert Frost, 1916 |
|
|
|
The Archimedian definition of a straight line as the shortest path between two points was an early expression of a variational principle, leading to the modern idea of a geodesic path. In the same spirit, Hero explained the paths of reflected rays of light based on a principle of least distance, which Fermat reinterpreted as a principle of least time, enabling him to account for refraction as well. Subsequently, Maupertius and others developed this approach into a general principle of least action, applicable to mechanical as well as optical phenomena. Of course, as discussed in Chapter 3.4, a more correct statement of these principles is that systems evolve along stationary paths, which may be maximal, minimal, or neither (at an inflection point). |
|
|
|
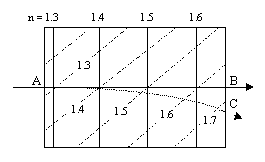
This is a tremendously useful principle, but as a realistic explanation it has always been at least slightly suspect, because (for example) it isn't clear how a single ray of light (or a photon) moving along a particular path can "know" that it is an extremal path in the variational sense. To illustrate the problem, consider a photon traveling from A to B through a transparent medium whose refractive index n increases in the direction of travel, as indicated by the solid vertical lines in the drawing below: |
|
|
|
|
|
|
|
Since the path AB is parallel to the gradient of the refractive index, it undergoes no refraction. However, if the lines of constant refractive index were tilted as shown by the dashed diagonal lines in the figure, a ray of light initially following the path AB will be refracted and arrive at C, even though the index of refraction at each point along the path AB is identical to what it was before, where there was no refraction. This shows that the path of a light ray cannot be explained solely in terms of the value of the refractive index the path. We must also consider the transverse values of the refractive index along neighboring paths, i.e., along paths not taken. |
|
|
|
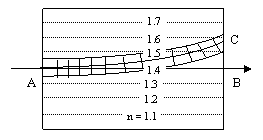
The classical wave explanation, proposed by Huygens, resolves this problem by denying that light can propagate in the form of a single ray. According to the wave interpretation, light propagates as a wave front possessing transverse width. A small section of a propagating wave front is shown in the figure below, with the gradient of the refractive index perpendicular to the initial trajectory of light: |
|
|
|
|
|
|
|
Clearly the wave front propagates more rapidly on the side where the refractive index is low (viz, the speed of light is high) than on the side where the refractive index is high. As a result, the wave front naturally turns in the direction of higher refractive index (i.e., higher density). It's easy to see that the amount of deflection of the normal to the wave front agrees precisely with the result of applying Fermat's principle, because the wave front represents a locus of points that are at an equal phase distance from the point of emission. Thus the normal to the wave front is, by definition, a stationary path in the variational sense. |
|
|
|
More generally, Huygens articulated the remarkable principle that every point of a wave front can be regarded as the origin of a secondary spherical wave, and the envelope of all these secondary waves constitutes the propagated wave front. This is illustrated in the figure below: |
|
|
|
|
|
|
|
Huygens also assumed the secondary wave originating at any point has the same speed and frequency as the primary wave at that point. The main defect in Huygens' wave theory of optics was it's failure to account for the ray-like properties of light, such as the casting of sharp shadows. Because of this failure (and also the inability of the wave theory to explain polarization), the corpuscular theory of light favored by Newton seemed more viable throughout the 18th century. However, early in the 19th century, Young and Fresnel modified Huygens' principle to include the crucial element of interference. The modified principle asserts that the amplitude of the propagated wave is determined by the superposition of all the (unobstructed) secondary wavelets originating on the wave front at any prior instant. (Young also proposed that light was a transverse rather than longitudinal wave, thereby accounting for polarization - but only at the expense of making it very difficult to conceive of a suitable material medium, as discussed in Chapter 3.5.) |
|
|
|
In his critique of the wave theory of light Newton (apparently) never realized that waves actually do exhibit "rectilinear motion", and cast sharp shadows, etc., provided that the wavelength is small on the scale of the obstructions. In retrospect, it's surprising that Newton, the superb experimentalist, never noticed this effect, since it can be seen in ordinary waves on the surface of a pool of water. Qualitatively, if the wavelength is large relative to an aperture, the phases of the secondary wavelets emanating from every point in the mouth of the aperture to any point in the region beyond will all be within a fraction of a cycle from each other, so they will (more or less) constructively reinforce each other. On the other hand, if the wavelength is very small in comparison with the size of the aperture, the region of purely constructive interference on the far side of the aperture will just be a narrow band perpendicular to the aperture. |
|
|
|
The wave theory of light is quite satisfactory for a wide range of optical phenomena, but when examined on a microscopic scale we find the transfer of energy and momentum via electromagnetic waves exhibits a granularity, suggesting that light comes in discrete quanta (packets). Planck had originated the quantum theory in 1900 by showing that the so-called ultra-violet catastrophe entailed by the classical theory of blackbody radiation (which predicted infinite energy at the high end of the spectrum) could be avoided - and the actual observed radiation could be accurately modeled - if we assume oscillators lining the walls of the cavity can absorb and emit electromagnetic energy only in discrete units proportional to the frequency, n. The constant of proportionality is now known as Planck's constant, denoted by h, and has the incredibly tiny value (6.626)10-34 Joule seconds. Thus a physical oscillator with frequency n emits and absorbs energy in integer multiples of hn. |
|
|
|
Planck's interpretation was that the oscillators were quantized, i.e., constrained to emit and absorb energy in discrete units, but he did not (explicitly) suggest that electro-magnetic energy itself was inherently quantized. However, in a sense, this further step was unavoidable, because ultimately light is nothing but its emissions and absorptions. It's not possible to "see" an isolated photon. The only perceivable manifestation of photons is their emissions and absorptions by material objects. Thus if we carry Planck's assumption to its logical conclusion, it's natural to consider light itself as being quantized in tiny bundles of energy hn. This was explicitly proposed by Einstein in 1905 as a heuristic approach to understanding the photoelectric effect. |
|
|
|
Incidentally, it was this work on the photoelectric effect, rather than anything related to special or general relativity, that was cited by the Nobel committee in 1921 when Einstein was finally awarded the prize. Interestingly, the divorce settlement of Albert and Mileva Einstein, negotiated through Einstein's faithful friend Besso in 1918, included the provision that the cash award of any future Nobel prize which Albert might receive would go to Mileva for the care of the children, as indeed it did. We might also observe that Einstein's work on the photoelectric effect was much more closely related to the technological developments leading to the invention of television than his relativity theory was to the unleashing of atomic energy. Thus, if we wish to credit or blame Einstein for laying the scientific foundations of a baneful technology, it might be more accurate to cite television rather than the atomic bomb. |
|
|
|
In any case, it had been known for decades prior to 1905 that if an electromagnetic wave shines on a metallic substance, which possesses many free valence electrons, some of those electrons will be ejected from the metal. However, the classical wave theory of light was unable to account for several features of this observed phenomena. For example, according to the wave theory the kinetic energy of the ejected electrons should increase as the intensity of the incident light is increased (at constant frequency), but in fact we observe that the ejected electrons invariably possess exactly the same kinetic energy for a given frequency of light. Also, the wave theory predicts that the photoelectric effect should be present (to some degree) at all frequencies, whereas we actually observe a definite cutoff frequency, below which no electrons are ejected, regardless of the intensity of the incident light. A more subtle point is that the classical wave theory predicts a smooth continuous transfer of energy from the wave to a particle, and this implies a certain time lag between when the light first strikes the metal and when electrons begin to be ejected. No such time lag is observed. |
|
|
|
Einstein's proposal for explaining the details of the photoelectric effect was to take Planck's quantum theory seriously, and consider the consequences of assuming that light of frequency n consists of tiny bundles - later given the name photons - of energy hn. Just as Planck had said, each material "oscillator" emits and absorbs energy in integer multiples of this quantity, which Einstein interpreted as meaning that material particles (such as electrons) emit and absorb whole photons. This is an extraordinary hypothesis, and might seem to restore Newton's corpuscular theory of light. However, these particles of light were soon found to possess properties and exhibit behavior quite unlike ordinary macroscopic particles. For example, in 1924 Bose gave a description of blackbody radiation using the methods of statistical thermodynamics based on the idea that the cavity is filled with a "gas" of photons, but the statistical treatment regards the individual photons as indistinguishable and interchangeable, i.e., not possessing distinct identities. This leads to the Bose-Einstein distribution |
|
|
|
|
|
|
|
which gives, for a system in equilibrium at temperature T, the expected number of particles in a quantum state with energy E. In this equation, k is Boltzman's constant and A is a constant determined by number of particles in the system. Particles that obey Bose-Einstein statistics are called Bosons. Compare this distribution with the classical Boltzman distribution, which applies to a collection of particles with distinct identities (such as complex atoms and molecules) |
|
|
|
|
|
|
|
A third equilibrium distribution arises if we consider indistinguishable particles that obey the Pauli exclusion principle, which precludes more than one particle from occupying any given quantum state in a system. Such particles are called fermions, the most prominent example being electrons. It is the exclusion principle that accounts for the variety and complexity of atoms, and their ability to combine chemically to form molecules. The energy distribution in an equilibrium gas of fermions is |
|
|
|
|
|
|
|
The reason photons obey Bose-Einstein rather than Fermi statistics is that they do not satisfy the Pauli exclusion principle. In fact, multiple bosons actually prefer to occupy the same quantum state, which led to Einstein's prediction of stimulated emission, the principle of operation behind lasers, which have become so ubiquitous today in CD players, fiber optic communications, and so on. Thus the photon interpretation has become an indispensable aspect of our understanding of light. |
|
|
|
However, it also raises some profound questions about our most fundamental ideas of space, time, and motion. First, the indistinguishability and interchangeability of fundamental particles (fermions as well as bosons) challenges the basic assumption that distinct objects can be identified from one instant of time to the next, which (as discussed in Chapter 1.1) underlies our intuitive concept of motion. Second, even if we consider the emission and absorption of just a single particle of light, we again face the question of how the path of this particle is chosen from among all possible paths between the emission and absorption events. We've seen that Fermat's principle of least time seems to provide the answer, but it also seems to imply that the photon somehow "knows" which direction at any given point is the quickest way forward, even though the knowledge must depend on the conditions at points not on the path being followed. Also, the principle presupposes either a fixed initial trajectory or a defined destination, neither of which is necessarily available to a photon at the instant of emission. |
|
|
|
In a sense, the principle of least time is backwards, because it begins by positing particular emission and absorption events, and infers the hypothetical path of a photon connecting them, whereas we should like (classically) to begin with just the emission event and infer the time and location of the absorption event. The principle of Fermat can only assist us if we assume a particular definite trajectory for the photon at emission, without reference to any absorption. Unfortunately, the assignment of a definite trajectory to a photon is highly problematical because, as noted above, a photon really is nothing but an emission and an associated absorption. To speak about the trajectory of a free photon is to speak about something that cannot, even in principle, ever be observed. |
|
|
|
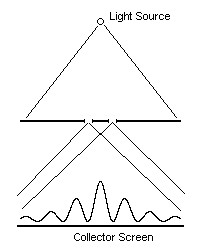
Moreover, many optical phenomena are flatly inconsistent with the notion of free photons with definite trajectories. The wavelike behavior of light, such as demonstrated in Young's two-slit interference experiment, defy explanation in terms of free particles of light moving along free trajectories independent of the emission and absorption events. The figure below gives a schematic of Young's experiment, showing that the intensity of light striking the collector screen exhibits the interference effects of the light emanating from the two slits in the intermediate screen. |
|
|
|
|
|
This interference pattern is easily explained in terms of interfering waves, but for light particles we expect the intensity on the collector screen to be just the sum of the intensities given by each slit individually. Still, if we regard the flow of light as consisting of a large number of photons, each with their own phases, we might be able to imagine that they somehow mingle with each other while passing from the source to the collector, thereby producing the interference pattern. However, the problem becomes more profound if we reduce the intensity of the light source to a sufficiently low level that we can actually detect the arrival of individual photons, like clicks on a Geiger counter, by an array of individual photo-detectors lining the collector screen. Each arrival is announced by just a single detector. We can even reduce the intensity to such a low level that no more than one photon is "in flight" at any given time. Under these conditions there can be no "mingling" of various photons, and yet if the experiment is carried on long enough we find that the number of arrivals at each point on the collector screen matches the interference pattern. |
|
|
|
The modern theory of quantum electrodynamics explains this behavior by denying that photons follow definite trajectories through space and time. Instead, an emitter has at each instant along its worldline a particular complex amplitude for emitting a photon, and a potential absorber has a complex amplitude for absorbing that photon. The amplitude at the absorber is the complex sum of the emission amplitudes of the emitter at various times in the past, corresponding to the times required to traverse each of the possible paths from the emitter to the absorber. At each of those times the light source had a certain complex amplitude for emitting a photon, and the phase of that amplitude advances steadily along the timeline of the emitter, giving a frequency equal to the frequency of the emitted light. |
|
|
|
For example, when we look at the reflection of a light source on a mirror our eye is at one end of a set of rays, each of slightly different length, which implies that amplitude for each path corresponds to the amplitude of the emitter at a slightly different time in the past. Thus, we are actually receiving an image of the light source from a range of times in the past. This is illustrated in the drawing below: |
|
|
|
|
|
|
|
If the optical path lengths of the bundle of incoming rays in a particular direction are all nearly equal (meaning that the path is "stationary" in the variational sense), their amplitudes will all be nearly in phase, so they reinforce each other, yielding a large complex sum. On the other hand, if the lengths of the paths arriving from a particular direction differ significantly, the complex sum of amplitudes will be taken over several whole cycles of the oscillating emitter amplitude, so they largely cancel out. This is why most of the intensity of the incoming ray arrives from the direction of the stationary path, which conforms with Hero's equi-angular reflection. |
|
|
|
To test the reality of this interpretation, notice that it claims the absence of reflected light at unequal angles is due to the canceling contributions of neighboring paths, so in theory we ought to be able to delete the paths corresponding to all but one phase angle of the emitter, and thereby enable us to see non-Heronian reflected light. This is actually the principle of operation of a diffraction grating, where alternating patches of a reflecting surface are scratched away, at intervals in proportion to the wavelength of the light. When this is done, it is indeed possible to see light reflected at highly non-Heronian angles, as illustrated below. |
|
|
|
|
|
|
|
All of this suggests that the conveyance of electromagnetic energy from an emitter to an absorber is not well-described in terms of a classical free particle following a free path through spacetime. It also suggests that what we sometimes model as wave properties of electromagnetic radiation are really wave properties of the emitter. This is consistent with the fact that the wave function of a putative photon does not advance along its null worldline. See Section 9.10, where it is argued that the concept of a "free photon" is meaningless, because every photon is necessarily emitted and absorbed. If we compare a photon to a clap, then a "free photon" is like clapping with no hands. |
|
|