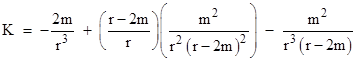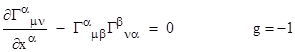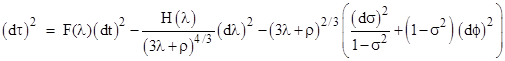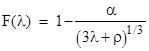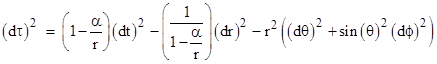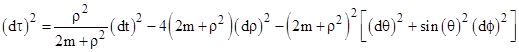|
|
|
It seemed that out of battle I escaped |
|
Down some profound dull tunnel... |
|
Willfred Owen (1893-1918) |
|
|
|
In the summer of 1913 Einstein accepted an offer of a professorship at the University of Berlin and membership in the Prussian Academy of Sciences. He left Zurich in the Spring of 1914, and his inaugural address before the Prussian Academy took place on July 2, 1914, just four days after the Austrian Archduke Franz Ferdinand was assasinated in Sarajevo. A month later, Germany was at war with Belgium, Russia, France, and Britain. Surprisingly, the world war did not prevent Einstein from continuing his intensive efforts to generalize the theory of relativity so as to make it consistent with gravitation − but his marriage almost did. By April of 1915 he was separated from his wife Mileva and their two young sons, who had once again taken up residence in Zurich. The marriage was not a happy one, and he later wrote to his friend Besso that if he had not kept Mileva at a distance, he would have been worn out, physically and emotionally. Besso and Fritz Haber (Einstein's close friend and colleague) both made efforts to reconcile Albert and Mileva, but without success. |
|
|
|
It was also during this period that Haber was working for the German government to develop poison gas for use in the war. On April 22, 1915 Haber directed the release of chlorine gas on the Western Front at Ypres in France. On May 23rd Italy declared war on Austria-Hungary, and subsequently against Germany itself. Meanwhile an Allied army was engaged in a disastrous campaign to take the Gallipoli Peninsula from Germany's ally, the Turks. Germany shifted the weight of its armies to the Eastern Front during this period, hoping to force Russia out of the war while fighting a holding action against the French and British in the West. In a series of huge battles from May to September the Austro-German armies drove the Russians back 300 miles, taking Poland and Lithuania and eliminating the threat to East Prussia. Despite these defeats, the Russians managed to re-form their lines and stay in the war (at least for another two years). The astronomer Karl Schwarzschild was stationed with the German Army in the East, but still kept close watch on Einstein's progress, which was chronicled like a serialized Dickens novel in almost weekly publications of the Berlin Academy. |
|
|
|
Toward the end of 1915, having failed to drive Russia out of the war, the main German armies were shifted back to the Western Front. Falkenhayn (the chief of the German general staff) was now convinced that a traditional offensive breakthrough was not feasible, and that Germany's only hope of ultimately ending the war on favorable terms was to engage the French in a war of attrition. His plan was to launch a methodical and sustained assault on a position that the French would feel honor-bound to defend to the last man. The ancient fortress of Verdun ("they shall not pass") was selected, and the plan was set in motion early in 1916. Falkenhayn had calculated that only one German soldier would be killed in the operation for every three French soldiers, so they would "bleed the French white" and break up the Anglo-French alliance. However, the actual casualty ratio turned out to be four Germans for every five French. By the end of 1916 a million men had been killed at Verdun, with no decisive change in the strategic position of either side, and the offensive was called off. |
|
|
|
At about the same time that Falkenhayn was formulating his plans for Verdun, on Nov 25, 1915, Einstein arrived at the final form of the field equations for general relativity. After a long and arduous series of steps (and missteps), he was able to announce that "finally the general theory of relativity is closed as a logical structure". Given the subtlety and complexity of the equations, one might have expected that rigorous closed-form solutions for non-trivial conditions would be difficult, if not impossible, to find. Indeed, Einstein's computations of the bending of light, the precession of Mercury's orbit, and the gravitational redshift were all based on approximate solutions in the weak field limit. However, just two months later, Schwarzschild had the exact solution for the static isotropic field of a mass point, which Einstein presented on his behalf to the Prussian Academy on January 16, 1916. Schwarzschild lived only another four months. He became ill at the front and died on May 11 at the age of 42. |
|
|
|
It's been said that Einstein was scandalized by Schwarzschild's solution, for two reasons. First, he still imagined that the general theory might be the realization of Mach's dream of a purely relational theory of motion, in which the inertia of a particle of matter is entirely determined by the relations to other matter. Schwarzschild’s solution gives a spherically symmetrical spacetime metric (inertial field) for a single mass point in an otherwise empty universe, determined largely by the boundary conditions at infinity, a result that Einstein regarded as inconsistent with “Mach’s Principle”. That such a situation could correspond to an exact solution of his field equations was worrisome to Einstein, and probably contributed to his eventual rejection of Mach's ideas. Second, the solution found by Schwarzschild − which was soon shown by Birkhoff to be the unique spherically symmetric solution to the field equations (barring a non-zero cosmological constant) − contained what looked like an unphysical singularity. Of course, since the source term was assumed to be an infinitesimal mass point, a singularity at r = 0 is perhaps not too surprising (noting that Newton's inverse square law is also singular at r = 0), but the metric coefficients of Schwarzschild solution are also singular at r = 2m, where m is the mass of the gravitating object in geometric units. |
|
|
|
Einstein and others argued that it wasn't physically realistic for a configuration of particles of total mass m to reside within their joint Schwarzschild radius r = 2m, so this "singularity" cannot exist in reality. However, subsequent analyses have shown that (barring some presently unknown physics) there is nothing to prevent a sufficiently massive object from collapsing to within its Schwarzschild radius, so it's worthwhile to examine the formal singularity at r = 2m to understand its physical significance. We find that the spacetime manifold at this boundary need not be considered as singular, because it can be shown that the singularity is removable, in the sense that all the invariant measures of the field smoothly approach fixed finite values as r approaches 2m from either direction. Thus we can analytically continue the solution through the singularity. |
|
|
|
Describing the Schwarzschild boundary as an "analytically removable singularity" is somewhat unconventional. It's customary to assert that the Schwarzschild solution is unequivocally non-singular at r = 2m, because the intrinsic curvature and proper time of a free-falling object are finite and well-behaved at that radius. Indeed we derived these facts in Section 6.4. However, it's worth remembering that even with respect to the proper frame of an in-falling test particle, there remains a formal singularity at r = 2m. (See the discussion in Section 6.4.) The free-falling coordinate system does not remove the singularity, but it makes the singularity analytically removable. Similarly our derivation in Section 6.4 of the intrinsic curvature K of the Schwarzschild solution at r = 2m tacitly glossed over the intermediate result |
|
|
|
|
|
Strictly speaking, the middle term on the right side is 0/0 (i.e., undefined) at r = 2m. Granted, we can divide the numerator and denominator by (r−2m), but this step is unambiguously valid only if (r−2m) is not equal to zero. If (r−2m) does equal zero, this cancelation is still possible, but it amounts to the analytic removal of a singularity. In addition, once we have removed this singularity, the resulting term is infinite, formally equal to the third term, which is also infinite, but with opposite sign. We then proceed to subtract the infinite third term from the infinite second term to arrive at the innocuous-looking finite result K = −2m/r3 at r = 2m. |
|
|
|
Naturally the form of the metric coefficients and their derivatives depends on the choice of coordinates, and in a sense we can attribute the troublesome behavior of the metric components at r = 2m to the unsuitability of the traditional Schwarzschild coordinates r,t at this location. From this we might be tempted to conclude that the Schwarzschild radius has no physical significance. This is true locally, but globally the Schwarzschild radius is physically significant, as the event horizon between two regions of the manifold. Hence it isn't surprising that, in terms of the r,t coordinates, we encounter singularities and infinities, because these coordinates are globally unique, viz., the Schwarzschild coordinate t is the essentially unique time coordinate for which the manifold is globally static. |
|
|
|
Incidentally, Schwarzschild’s paper actually gave the solution of the static spherical vacuum field equations in terms of two different systems of coordinates. One of these is what we today call ‘Schwarzschild coordinates’, and the other was identical except for an arbitrary shift of the radial coordinate. His derivation was based on Einstein’s paper of 18 November 1915, so the field equations didn’t yet contain the trace term, but this didn’t affect Schwarzschild’s result since he was solving the vacuum equations, which simply entail the vanishing of the Ricci tensor. Following Einstein, Schwarzschild sought to solve the simplified field equations |
|
|
|
|
|
|
|
which (as discussed in Section 5.8) are valid only if the determinant g of the metric is constant. Like Einstein (at this time), Schwarzschild thought the condition g = −1 was necessary in order for the field equations to apply. Only later was it realized that this is simply a condition that can be imposed on the coordinates to enable the use of simplified field equations, whereas the vanishing of the full Ricci tensor represents fully covariant field equations (for the vacuum) with no coordinate conditions, i.e., the field equations are not restricted to “unimodular” metrics. |
|
|
|
Schwarzschild began by considering the most general spherically symmetrical polar line element whose coefficients are independent of the time coordinate and for which the metrical area of the surface of simultaneous events at constant radial coordinate r is 4πr2, which can be written as |
|
|
|
|
|
|
|
where f and h are arbitrary functions of the radial coordinate r. (Schwarzschild also posited an arbitrary factor on the angular terms of the metric, but that was superfluous.) The determinant g of a diagonal metric is simply the product of the coefficients, so for this metric we have g = −f(r) h(r) r2 sin(θ)2. This would result in an extremely complicated and unwieldy condition if we set g = −1 to enable the use of the simplified field equations. To simplify the determinant condition, Schwarzschild defined two new coordinates |
|
|
|
|
|
|
|
where ρ is an arbitrary constant. (Schwarzschild didn’t introduce this constant until later, but it simplifies the derivation to introduce it at the start.) It’s worth noting that λ varies as the cube of r, so it differs drastically from any intuitive concept of a measure of radial distance. In any case, from this we get the differentials |
|
|
|
|
|
|
|
Substituting these into the general line element gives the transformed line element |
|
|
|
|
|
|
|
where F(λ) = f(r) and H(λ) = h(r). This metric has the determinant g = −F(λ)H(λ). Setting this equal to −1, we have the condition H(λ) = 1/F(λ). In order for the simplified Ricci tensor to vanish for this metric, and for the metric to approach flat Minkowski spacetime at sufficiently large distances, we must have |
|
|
|
|
|
|
|
where α is a constant of integration which must equal 2m to give the correct Newtonian limit. Hence, remembering that r = (3λ+ρ)1/3 and dλ = r2dR, we can substitute into the metric and revert back to the θ coordinate to give what is now called the Schwarzschild metric |
|
|
|
|
|
|
|
The metric coefficients are singular at r = α and r = 0. Now, Schwarzschild thought the singularity at r = α ought to occur at λ = 0, so he set ρ = α3. It follows that the singularity at r = 0 occurs at λ = −α3/3. This is certainly permissible, but there is no compelling reason to place the singularities at any particular values of the λ coordinate, and in any case it doesn’t affect the solution. (Note that in terms of the coordinates t,λ,σ,ϕ the metric coefficients are singular at σ = 0 and π for all radial positions, but this is obviously just due to a singularity in the coordinates, not in the metrical relations in the manifold.) |
|
|
|
Schwarzschild also proposed another radial coordinate, which we will call R, defined as R = (r3−α3)1/3, so the singularities in the metric components occur at R = 0 and R = −α. (In Schwarzschild’s paper the symbols r and R are swapped, but we use r to denote the usual radial Schwarzschild coordinate for consistency.) Again, this is permissible, but it doesn’t affect any of the metrical relations on the manifold, it merely relabels the events. For example, with this radial coordinate the area of the surface of constant radial coordinate R is equal to 4π(R3+α3)2/3, not 4πR2. In particular, at R = 0 the surface area is 4πα2, so it is certainly not a single point. |
|
|
|
Schwarzschild’s discussion of alternative coordinate systems has sometimes misled people (perhaps even himself) into thinking that they represents physically distinct solutions. This is obviously not true, because we can translate from one metric to the other simply by substituting the transformations from one set of coordinates to the other. Admittedly for Schwarzschild’s alternate radial coordinate R we can define quasi-orthogonal coordinates |
|
|
|
|
|
|
|
in terms of which X = Y = Z = 0 when R = 0, but just as the X,Y,Z coordinates take on negative values at various points of the manifold, nothing prevents us from extending the solution to negative values of the R coordinate, at least not until we arrive at the condition R = −α. At this location we have a genuine singularity in the manifold, because the curvature scalar becomes infinite. |
|
|
|
In terms of these alternate coordinates the entire surface of the Schwarzschild horizon has the same spatial coordinates X = Y = Z = 0, but this does not imply that it is a single point. Rather, these coordinates are ill-conditioned at this radius. It may seem that as we pass into negative values of X,Y,Z we simply increase R again, but this overlooks the duality of solutions to |
|
|
|
|
|
|
|
The distinction between the regions of positive and negative R is more clearly shown in terms of polar coordinates, because the point in the equatorial plane with polar coordinates R,0 need not be identified with the point −R,π. Essentially polar coordinates cover two separate planes, one with positive R and the other with negative R, and the only smooth paths between them are through the boundary at R = 0, which is the event horizon, whereas the physical singularity in the manifold occurs at the radial coordinate R = −α. In other words, the singularity at the "center" of the Schwarzschild solution occurs inside of the spherical surface at R = 0 of these polar coordinates. We can shift this boundary point arbitrarily by simply shifting the "zero point" of the complete R scale, which actually extends from −∞ to +∞. None of this changes any of the proper intervals along any physical paths, which are invariant under arbitrary (diffeomorphic) transformations. So the metric relations in terms of Schwarzschild's alternate coordinates are not physically distinct from those the usual interpretation, as explained by Johannes Droste in 1917. |
|
|
|
Furthermore, a singularity of the metric coefficients is not generally indicative of a singularity in the manifold itself, as shown by the usual latitude and longitude coordinates at the North Pole. Schwarzschild probably meant to impose continuity on the manifold itself, rather than on the coordinates and corresponding metric, but as Einstein remarked, "it is not so easy to free one's self from the idea that coordinates must have a direct metric significance". We also note that the coefficient of (dσ)2 in the metric in terms of Schwarzschild’s unimodular coordinates goes to infinity at σ = ±1, which corresponds to θ = 0 and π. Thus, in terms of those coordinates, the metric coefficients are drastically singular at all radial positions. This should have made it clear to Schwarzschild that a coordinate singularity does not imply any (local) singularity of the manifold. |
|
|
|
Interestingly, as late as 1936 (two decades after Schwarzschild's death) Einstein himself proposed to eliminate the coordinate singularity in the Schwarzschild metric by defining a radial coordinate r in terms of the usual Schwarzschild coordinate r by the relation ρ2 = r−2m. In terms of this coordinate the line element is |
|
|
|
|
|
|
|
Einstein notes that as r ranges from −∞ to +∞ the corresponding values of r range from +∞ down to 2m and them back to +∞, so he conceives of the complete solution as two identical sheets of physical space connected by the "bridge" at the boundary ρ = 0, where r = 2m and the determinant of the metric vanishes. This is called the Einstein-Rosen bridge. For values of r less than 2m he argues that "there are no corresponding real values of ρ". On this basis he asserts that the region r < 2m has been excluded from the solution. However, this is really just another re-expression of the original Schwarzschild solution, describing the "exterior" portions of the solution, but neglecting the interior portion, where ρ is imaginary. Just as we can allow Schwarzschild's r to take on negative values, we can allow Einstein's r to take on imaginary values. The maximal analytic extension of the Schwarzschild solution necessarily includes the interior region, and it can't be eliminated simply by a change of variables. Ironically, the reason the manifold seems to be well-behaved across Einstein's "bridge" between the two exterior regions while jumping over the interior region is precisely that the r coordinate is locally ill-behaved at ρ = 0. Birkhoff proved that the Schwarzschild solution is the unique spherically symmetrical solution of the field equations, and it has been shown that the maximal analytic extension of this solution (called the Kruskal extension, discussed in Section 6.4) consists of two exterior regions connected by the internal region, and contains a genuine manifold singularity. |
|
|
|
On the other hand, just because the maximally extended Schwarzschild solution satisfies the field equations, it doesn't necessarily follow that such a thing exists. In fact, there is no known physical process that would produce two asymptotically flat regions of spacetime connected at a singularity, and there is no reason to believe that such a thing would ever happen. In contrast, it's fairly plausible that some part of the complete Schwarzschild solution could be produced, such as by the collapse of a sufficiently massive star. The implausibility of the maximally extended solutions doesn't preclude the existence of black holes − although it does remind us to be cautious about assuming the actual existence of things just because they are solutions of the field equations. |
|
|
|
Despite the implausibility of an Einstein-Rosen bridge connecting two distinct sheets of spacetime, this idea has recently gained widespread attention, the term "bridge" having been replaced with "wormhole". It's been speculated that under certain exotic conditions it might be possible to actually traverse a wormhole, passing from one region of spacetime to another. As discussed above this is definitely not possible for the classical Schwarzschild solution, because of the unavoidable singularity, but people have recently explored the possibilities of traversable wormholes. Naturally if such direct conveyance between widely separate regions of spacetime were possible, and if those regions were also connected by (much longer) ordinary time-like paths, this raises the prospect of various kinds of "time travel", assuming a wormhole connected to the past was somehow established and maintained. However, these rather far-fetched scenarios all rely on the premise of negative energy density, which of course violates the so-called "null energy condition", not to mention the weak, strong, and dominant energy conditions of classical relativity. In other words, on the basis of classical relativity and the traditional energy conditions we could rule out traversable wormholes altogether. It is only the fact that some quantum phenomena do apparently violate these energy conditions (albeit very slightly) that leaves open the remote possibility of such things. |
|
|