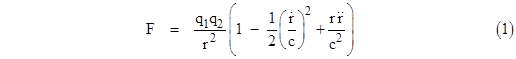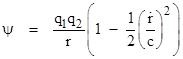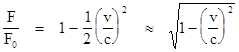8.6† On Gauss's Mountains |
|
|
|
Grossmann is getting his doctorate on a topic that is connected with fiddling around and non-Euclidean geometry. I donít know exactly what it is. |
|
†††††††††††††††††††††††††††††††††††††††††††† Einstein to Mileva Maric, 1902 |
|
|
|
One of the most famous stories about Gauss depicts him measuring the angles of the great triangle formed by the mountain peaks of Hohenhagen, Inselberg, and Brocken for evidence that the geometry of space is non-Euclidean. It's certainly true that Gauss acquired geodetic survey data during his ten-year involvement in mapping the Kingdom of Hanover during the years from 1818 to 1832, and this data included some large "test triangles", notably the one connecting the those three mountain peaks, which could be used to check for accumulated errors in the smaller triangles. It's also true that Gauss understood how the intrinsic curvature of the Earth's surface would theoretically result in slight discrepancies when fitting the smaller triangles inside the larger triangles, although in practice this effect is negligible, because the Earth's curvature is so slight relative to even the largest triangles that can be visually measured on the surface. Still, Gauss computed the magnitude of this effect for the large test triangles because, as he wrote to Olbers, "the honor of science demands that one understand the nature of this inequality clearly". (The government officials who commissioned Gauss to perform the survey might have recalled Napoleon's remark that Laplace as head of the Department of the Interior had "brought the theory of the infinitely small to administration".) It is sometimes said that the "inequality" which Gauss had in mind was the possible curvature of space itself, but taken in context it seems he was referring to the curvature of the Earth's surface. |
|
|
|
On the other hand, if the curvature of space was actually great enough to be observed in optical triangles of this size, then presumably Gauss would have noticed it, so we may still credit him with having performed an empirical observation of geometry, but in this same sense every person who ever lived has made such observations. It might be more meaningful to name people who have explicitly argued against the empirical status of geometry, i.e., who have claimed that the character of spatial relations could be known without empirical observation. In his "Critique of Pure Reason", Kant famously declared that Euclidean geometry is the only possible way in which the mind can organize information about extrinsic spatial relations. One could also cite Plato and other idealists and a priorists. On the other hand, Poincare advocated a conventionalist view of geometry, arguing that we can always, if we wish, cast our physics within a Euclidean spatial framework - provided we are prepared to make whatever adjustments in our physical laws are necessary to preserve this convention. In any case, it seems reasonable to agree with Buhler, who concludes in his biography of Gauss that "the oft-told story according to which Gauss wanted to decide the question [of whether space is perfectly Euclidean] by measuring a particularly large triangle is, as far as we know, a myth." |
|
|
|
The first person to publicly propose an actual test of the geometry of space was apparently Lobachevski, who suggested that one might "investigate a stellar triangle for an experimental resolution of the question." The "stellar triangle" he proposed was the star Sirius and two different positions of the Earth at 6-month intervals. This was used by Lobachevski as an example to show how we could place limits on the deviation from flatness of actual space, based on the fact that, in a hyperbolic space of constant curvature, there is a limit to how small a star's parallax can be, even the most distant star. Gauss had already (in private correspondence with Taurinus in 1824) defined the "characteristic length" of a hyperbolic space, which he called "k", and had derived several formulas for the properties of such a space in terms of this parameter. For example, the circumference of a circle of radius r in a hyperbolic space whose "characteristic length" is k is given by |
|
|
|
|
|
|
|
Since sinh(x) = x + x3/3! +..., it follows that C approaches 2πr as k increases to infinity. From the fact that the maximum parallax of Sirius (as seen from the Earth at various times) is 1",24, Lobachevski deduced that the value of k for our space must be at least 166,000 times the radius of the Earth's orbit. Naturally the same analysis for more distant stars gives an even larger lower bound on k. |
|
|
|
The first definite measurement of parallax for a fixed star was performed by Friedrich Bessel (a close friend of Gauss) in 1838, on the star 61 Cygni. Shortly thereafter he measured Sirius (and discovered its binary nature). Lobachevski's first paper on "the new geometry" was presented as a lecture at Kasan in 1826, followed by publications in 1829, 1835, 1840, and 1855 (a year before his death). He presented his lower bound on "k" in the later editions based on the still fairly recent experimental results of stellar parallax measurements. In 1855 Lobachevski was completely blind, so he dictated his exposition. |
|
|
|
The other person credited with discovering non-Euclidean geometry, Janos Bolyai, was the son of Wolfgang Bolyai, who was a friend (almost the only friend) of Gauss during their school days at Gottingen in the late 1790's. The elder Bolyai had also been interested in the foundations of geometry, and spent many years trying to prove that Euclid's parallel postulate is a consequence of the other postulates. Eventually he concluded that it had been a waste of time, and he became worried when his son Janos became interested in the same subject. The alarmed father wrote to his son |
|
|
|
For God's sake, I beseech you, give it up. Fear it no less than sensual passions because it, too, may take all your time, and deprive you of your health, peace of mind, and happiness in life. |
|
|
|
Undeterred, Janos continued to devote himself to the study of the parallel postulate, and in 1829 he succeeded in proving just the opposite of what his father (and so many others) had tried in vain to prove. Janos found (as had Gauss, Taurinnus, and Lobachevesky just a few years earlier) that Euclid's parallel postulate is not a consequence of the other postulates, but is rather an independent assumption, and that alternative but equally consistent geometries based on different assumptions may be constructed. He called this the "Absolute Science of Space", and wrote to his father that "I have created a new universe from nothing". The father then, forgetting his earlier warnings, urged Janos to publish his findings as soon as possible, noting that |
|
|
|
...ideas pass easily from one to another, and secondly... many things have an epoch, in which they are found at the same time in several places, just as violets appear on every side in spring. |
|
|
|
Naturally the elder Bolyai sent a copy of his son's spectacular discovery to Gauss, in June of 1831, but it was apparently lost in the mail. Another copy was sent in January of 1832, and then seven weeks later Gauss sent a reply to his old friend: |
|
|
|
If I commenced by saying that I am unable to praise this work, you would certainly be surprised for a moment. But I cannot say otherwise. To praise it would be to praise myself. Indeed the whole contents of the work, the path taken by your son, the results to which he is led, coincide almost entirely with my meditations, which have occupied my mind partly for the last thirty or thirty-five years. So I remained quite stupefied. So far as my own work is concerned, of which up till now I have put little on paper, my intention was not to let it be published during my lifetime. ... I have found very few people who could regard with any special interest what I communicated to them on this subject. ...it was my idea to write down all this later so that at least it should not perish with me. It is therefore a pleasant surprise for me that I am spared this trouble, and I am very glad that it is just the son of my old friend, who takes the precedence of me in such a remarkable manner. |
|
|
|
In his later years Gauss' response to many communications of new mathematical results was similar to the above. For example, he once remarked that a paper of Abel's saved him the trouble of having to publish about a third of his results concerning elliptic integrals. Likewise he confided to friends that Jacobi and Eisenstein had "spared him the trouble" of publishing important results that he (Gauss) had possessed since he was a teenager, but had never bothered to publish. Dedekind even reports that Gauss made a similar comment about Riemann's dissertation. It's true that Gauss' personal letters and notebooks substantiate to some extent his private claims of priority for nearly every major mathematical advance of the 19th century, but the full extent of his early and unpublished accomplishments did not become known until after his death, and in any case it wouldn't have softened the blow to his contemporaries. Janos Bolyai was so embittered by Gauss's backhanded response to his non-Euclidean geometry that he never published again. |
|
|
|
As another example of what
Wolfgang Bolyai called "violets appearing on every side", Maxwell's
great 1865 triumph of showing that electromagnetic waves propagate at the
speed of light was, to some degree, anticipated by others. In 1848 Kirchoff
had noted that the ratio of electromagnetic and electrostatic units was equal
to the speed of light, although he gave no explanation for this coincidence. In
1858 Riemann presented a theory based on the hypothesis that electromagnetic
effects propagate at a fixed speed, and then deduced that this speed must
equal the ratio of electromagnetic and electrostatic units, i.e., |
|
|
|
Even in this field we find that Gauss can plausibly claim priority for some interesting developments. Recall that, in addition to being the foremost mathematician of his day, Gauss was also prominent in studying the phenomena of electricity and magnetism (in fact the unit of magnetism is called a Gauss), and even dabbled in electrodynamics. As mentioned in Section 3.5, he reached the conclusion that the keystone of electrodynamics would turn out to depend on an understanding of how electric effects propagate in time. In 1835 he wrote (in an unpublished papers, discovered after his death) that |
|
|
|
Two elements of electricity in a state of relative motion attract or repel one another, but not in the same way as if they are in a state of relative rest. |
|
|
|
He even suggested the following mathematical form for the complete electromagnetic force F between two particles with charges q1 and q2 in arbitrary states of motion |
|
|
|
|
|
|
|
where r is the scalar distance, r is the vector distance, u is the relative velocity between the particles, and dots signify derivatives with respect to time. This formula actually gives the correct results for particles in uniform (inertial) motion, in which case the second derivative of the vector r is zero. However, the dot product in Gaussís formula violates conservation of energy for general motions. A few years later (in 1845), Gaussís friend Wilhelm Weber proposed a force law identical to Gaussís, except he excluded the dot product, i.e., he proposed the formula |
|
|
|
|
|
|
|
Weber pointed out that, unlike Gaussís original formula, this force law satisfies conservation of energy, as shown by the fact that it can be derived from the potential function |
|
|
|
|
|
|
|
In terms of this potential, the force given by F = Ėdψ/dr is precisely Weberís force law. Equation (1) was used by Weber as the basis of his theory of electrodynamics published in 1846. Indeed this formula served as the basis for most theoretical studies of electromagnetism until it was finally superseded by Maxwell's theory beginning in the 1870s. Itís interesting that in order for energy to be conserved it was necessary to eliminate the vectors from Gaussís formula, making the result entirely in terms of the scalar distance and its derivatives. Compare this with the separation equations discussed in Sections 4.2 and 4.4. Note that according to (1) the condition for the force between two charged particles to vanish is that the quantity in parentheses equals zero, i.e., |
|
|
|
|
|
|
|
Differentiating both sides
and dividing by r gives the condition |
|
|
|
|
|
|
|
So, to press the point, one could argue that Gauss' offhand suggestion for the formula expressing electrodynamic force already represents the seeds of Lorentz's molecular force hypothesis, from which follows the length contraction and time dilation of the Lorentz transformations and special relativity. In fact, pursuing this line of thought, Riemann (one of Gaussí successors at Gottingen) proposed in 1858 that the electric potential should satisfy the equation |
|
|
|
|
|
|
|
where ρ is the charge density. This equation does indeed give the retarded electrostatic potential, which, combined with the similar equation for the vector potential, serves as the basis for the whole classical theory of electromagnetism. Assuming conservation of charge, the invariance of the Minkowski spacetime metric clearly emerges from this equation, as does the invariance of the speed of light in terms of any suitable (i.e., inertially homogeneous and isotropic) system coordinates. |
|
|