|
8.1 Kepler, Napier, and the Third Law |
|
|
|
There is special providence in the fall of a sparrow. |
|
Shakespeare |
|
|
|
By the year 1605 Johannes Kepler, working with the relativistic/inertial view of the solar system suggested by Copernicus, had already discerned two important mathematical regularities in the orbital motions of the planets: |
|
|
|
I. Planets move in ellipses with the Sun at one focus. |
|
II. The radius vector describes equal areas in equal times. |
|
|
|
This shows the crucial role that interpretations and models sometimes play in the progress of science, because it's obvious that these profoundly important observations could never even have been formulated in terms of the Ptolemaic earth-centered model. |
|
|
|
Oddly enough, Kepler arrived at these conclusions in reverse order, i.e., he first determined that the radius vector of a planet's "oval shaped" path sweeps out equal areas in equal times, and only subsequently determined that the "ovals" were actually ellipses. It's often been remarked that Kepler's ability to identify this precise shape from its analytic properties was partly due to the careful study of conic sections by the ancient Greeks, particularly Apollonius of Perga, even though this study was conducted before there was even any concept of planetary orbits. Thus Kepler's first law is often cited as an example of how purely mathematical ideas (e.g., the geometrical properties of conic sections) can sometimes find significant applications in the descriptions of physical phenomena. |
|
|
|
After painstakingly extracting the above two "laws" of planetary motion (first published in 1609) from the observational data of Tycho Brahe, there followed a period of more than twelve years during which Kepler exercised his ample imagination searching for any further patterns or regularities in the data. He seems to have been motivated by the idea that the orbits of the planets must satisfy a common set of simple mathematical relations, analogous to the mathematical relations which the Pythagoreans had discovered between harmonious musical tones. However, despite all his ingenious efforts during these years, he was unable to discern any significant new pattern beyond the two empirical laws which he had found in 1605. Then, as Kepler later recalled, on the 8th of March in the year 1618, something marvelous "appeared in my head". He suddenly realized that |
|
|
|
III. The proportion between the periodic times of any two planets is precisely one and a half times the proportion of the mean distances. |
|
|
|
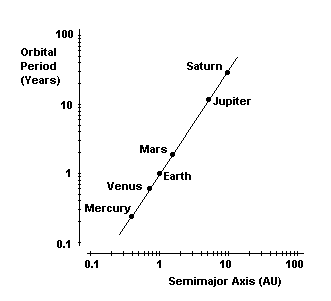
Presumably he used the word “proportion” here to signify the logarithm of the ratio, so he is asserting that log(T1/T2) = (3/2)log(r1/r2), where Tj are the periods and rj are the mean radii of the orbits of any two planets. In the form of a diagram, his insight looks like this: |
|
|
|
|
|
|
|
At first it may seem surprising that it took a mathematically insightful man like Kepler over twelve years of intensive study to notice this simple linear relationship between the logarithms of the orbital periods and radii. In modern data analysis the log-log plot is a standard format for analyzing physical data. However, we should remember that logarithmic scales had not yet been invented in 1605. A more interesting question is why, after twelve years of struggle, this way of viewing the data suddenly "appeared in his head" early in 1618. (Kepler made some errors in the calculations in March, and decided the data didn't fit, but two months later, on May 15 the idea "came into his head" again, and this time he got the computations right, and thought he was dreaming because the fit is so exact.) |
|
|
|
Is it just coincidental that John Napier's "Mirifici Logarithmorum Canonis Descripto" (published in 1614) was first seen by Kepler towards the end of the year 1616? We know that Kepler was immediately enthusiastic about logarithms, which is not surprising, considering the masses of computation involved in preparing the Rudolphine Tables. Indeed, he even wrote a book of his own on the subject in 1621. It's also interesting that Kepler initially described his "Third Law" in terms of a 1.5 ratio of proportions, exactly as it would appear in a log-log plot, rather than in the more familiar terms of squared periods and cubed distances. It seems as if a purely mathematical invention, namely logarithms, whose intent was simply to ease the burden of manual arithmetical computations, may have led directly to the discovery/formulation of an important physical law, i.e., Kepler's third law of planetary motion. (Ironically, Kepler's academic mentor, Michael Maestlin, chided him − perhaps in jest? − for even taking an interest in logarithms, remarking that "it is not seemly for a professor of mathematics to be childishly pleased about any shortening of the calculations".) By the 18th of May, 1618, Kepler had fully grasped the logarithmic pattern in the planetary orbits: |
|
|
|
Now, because 18 months ago the first dawn, three months ago the broad daylight, but a very few days ago the full Sun of a most highly remarkable spectacle has risen, nothing holds me back. |
|
|
|
It's interesting to compare this with Einstein's famous comment about "...years of anxious searching in the dark, with their intense longing, the final emergence into the light--only those who have experienced it can understand it". |
|
|
|
Kepler announced his Third Law in Harmonices Mundi, published in 1619, and also included it in his "Ephemerides" of 1620. The latter was actually dedicated to Napier, who had died in 1617. The cover illustration showed one of Galileo's telescopes, the figure of an elliptical orbit, and an allegorical female (Nature?) crowned with a wreath consisting of the Naperian logarithm of half the radius of a circle. It has usually been supposed that this work was dedicated to Napier in gratitude for the "shortening of the calculations", but Kepler obviously recognized that it went deeper than this, i.e., that the Third Law is purely a logarithmic harmony. In a sense, logarithms played a role in Kepler's formulation of the Third Law analogous to the role of Apollonius' conics in his discovery of the First Law, and with the role that tensor analysis and Riemannian geometry played in Einstein's development of the field equations of general relativity. In each of these cases we could ask whether the mathematical structure provided the tool with which the scientist was able to describe some particular phenomenon, or whether the mathematical structure effectively selected an aspect of the phenomena for the scientist to discern. |
|
|
|
Just as we can trace Kepler's Third Law of planetary motion back to Napier's invention of logarithms, we can also trace Napier's invention back to even earlier insights. It's no accident that logarithms have applications in the description of Nature. Indeed in his introduction to the tables, Napier wrote |
|
|
|
A logarithmic table is a small table by the use of which we can obtain a knowledge of all geometrical dimensions and motions in space... |
|
|
|
The reference to motions in space is very appropriate, because Napier originally conceived of his "artificial numbers" (later renamed logarithms, meaning number of the ratio) in purely kinematical terms. In fact, his idea can be expressed in a form that Zeno of Elea would have immediately recognized. Suppose two runners leave the starting gate, travelling at the same speed, and one of them maintains that speed, whereas the speed of the other drops in proportion to his distance from the finish line. The closer the second runner gets to the finish line, the slower he runs. Thus, although he is always moving forward, the second runner never reaches the finish line. As discussed in Section 3.7, this is exactly the kind of scenario that Zeno exploited to illustrate paradoxes of motion. Here, 2000 years later, we find Napier making very different use of it, creating a continuous mapping from the real numbers to his "artificial numbers". With an appropriate choice of units we can express the position x of the first runner as a function of time by x(t) = t, and the position X of the second runner is defined by the differential equation dX/dt = 1 − X where the position "1" represents the finish line. The solution of this equation is X(t) = 1 − e−t, where ex is the function that equals its own derivative. Then Napier defined x(t) as the "logarithm" of 1 − X(t), which is to say, he defined t as the "logarithm" of e−t. The definition of logarithm was subsequently revised so that we now define t as the logarithm of et, the latter being the function that equals its own derivative. |
|
|
|
The logarithm was one of many examples throughout history of ideas that were "in the air" at a certain time. It had been known since antiquity that the exponents of numbers in a geometric sequence are additive when terms are multiplied together, i.e., we have anam = a(m+n). In fact, there are ancient Babylonian tablets containing sequences of powers and problems involving the determination of the exponents of given numbers. In the 1540's Stifel's "Arithmetica integra" included tables of the successive powers of numbers, which was very suggestive for Napier and others searching for ways to reduce the labor involved in precise manual computations. |
|
|
|
In the 1580's Viete derived several trigonometric formulas such as |
|
|
|
|
|
If we have a table of cosine values this formula enables us to perform multiplication simply by means of addition. For example, to find the product of 0.7831 and 0.9348 we can set cos(x) = 0.7831 and cos(y) = 0.9348 and then look up the angles x,y with these cosines in the table. We find x = 0.67116 and y = 0.36310, from which we have the sum x+y = 1.03426 and the difference x−y = 0.30806. The cosines of the sum and difference can then be looked up in the table, giving cos(x+y) = 0.51116 and cos(x−y) = 0.95292. Half the sum of these two numbers equals the product 0.73204 of the original two numbers. This technique was called prosthaphaeresis (the Greek word for addition and subtraction), and was quickly adopted by scientists such as the Dane Tycho Brahe for performing astronomical calculations. Today we recognize that the above formula is just a disguised version of the simple exponent addition rule, noting that cos(x) = (eix + e−ix)/2. |
|
|
|
At about this same time (1594), John Napier was inventing his logarithms, whose purpose was also to reduce multiplication and division to simple addition and subtraction by means of a suitable transformation. However, Napier might never have set aside his anti-Catholic polemics to work on producing his table of logarithms had it not been for an off-hand comment made by Dr. John Craig, who was the physician to James VI of Scotland (later James I of England and Ireland). In 1590 Craig accompanied James and his entourage bound for Norway to meet his prospective bride Anne, who was supposed to have journeyed from Denmark to Scotland the previous year, but had been diverted by a terrible storm and ended up in Norway. (The storm was so severe that several supposed witches were held responsible and were burned.) James' party, too, encountered severe weather, but eventually he met Anne in Oslo and the two were married. On the journey home the royal party visited Tycho Brahe's observatory on the island of Hven, and were entertained by the famous astronomer, well known as the discoverer of the "new star" in the constellation Cassiopeia. During this stay at Brahe's lavish Uraneinborg ("castle in the sky") Dr. Craig observed the technique of prosthaphaeresis that Brahe and his assistants used to ease the burden of calculation. When he returned to Scotland, Craig mentioned this to his friend the Baron of Murchiston (aka John Napier), and this seems to have motivated Napier to devote himself to the development of his logarithms and the generation of his tables, on which he spent the remaining 25 years of his life. During this time Napier occasionally sent preliminary results to Brahe for comment. |
|
|
|
Several other people had similar ideas about exploiting the exponential mapping for purposes of computation. Indeed, Kepler's friend and assistant Jost Burgi evidently devised a set of "progress tables" (basically anti-logarithm tables) around 1600, based on the indices of geometric progressions, and made some use of these in his calculations. However, he didn't fully perceive the potential of this correspondence, and didn't develop it very far. |
|
|
|
Incidentally, if the story of a group of storm-tossed nobles finding themselves on a mysterious island ruled over by a magician sounds familiar, it may be because of Shakespeare's "The Tempest", written in 1610. This was Shakespeare's last complete play and, along with Love's Labor's Lost, his only original plot, i.e., these are the only two of his plays whose plots are not known to have been based on pre-existing works. It is commonly believed that the plot of "The Tempest" was inspired by reports of a group of colonists bound for Virginia who were shipwrecked in Bermuda in 1609. However, Shakespeare may also have had in mind the story of James VI (who by 1610 was James I, King of England) and his marriage expedition, arriving after a series of violent storms on the island of the Danish astronomer and astrologer Tycho Brahe and his “castle in the sky” (which included a menagerie of exotic animals). We know "The Tempest" was produced at the royal court in 1611 and again in 1612 as part of the festivities preceding the marriage of the King's daughter, and it seems possible that a story involving a tempest might evoke memories of the great storms of 1589 and 1590 that delayed Anne's voyage to Scotland and prompted James' journey to meet her. The providential aspects of Shakespeare's "The Tempest" and its parallels with their own experiences could hardly have been lost on them. (Incidentally, Kepler dedicated Harmonice Mundi to James I.) |
|
|
|
Shakespeare's choice of the peculiar names Rosencrantz and Guildenstern for two minor characters in "Hamlet, Prince of Denmark" gives further support to the idea that he was familiar with Tycho, since those were the names of two of Tycho's ancestors appearing on his coat of arms. There is also evidence that Shakespeare was personally close to the Digges family (e.g., Leonard Digges contributed a sonnet to the first Folio), and Thomas Digges was an English astronomer and mathematician who, along with John Dee, was well acquainted with Tycho. Digges was an early supporter and interpreter of Copernicus' relativistic ideas, and was apparently the first to suggest that our Sun was just an ordinary star in an infinite universe of stars. |
|
|
|
Considering all this, it may not be too far-fetched to suggest that Tycho was one of the models for Prospero, whose name, being composed of Providence and sparrow, is an example of Shakespeare's remarkable ability to weave a variety of ideas, influences, and connotations into the fabric of his plays, just as we can see in Kepler's three laws the synthesis of the heliocentric model of Copernicus, Apollonius' conics, and the logarithms of Napier. |
|
|