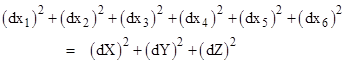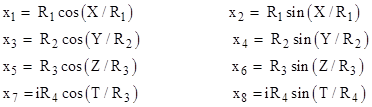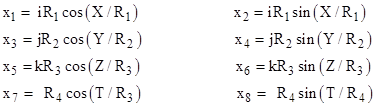|
7.4† Curled-Up Dimensions |
|
|
|
I do not mind confessing that I personally have often found relief from the dreary infinities of homaloidal space in the consoling hope that, after all, this other may be the true state of things. |
|
††††††††††††††††††††††††††††††† William Kingdon Clifford, 1873 |
|
|
|
The simplest cylindrical space can be represented by the perimeter of a circle of radius R. This one-dimensional space with the coordinate X has the natural embedding in two-dimensional space with orthogonal coordinates (x1,x2) given by the circle formulas |
|
|
|
|
|
From the derivatives dx1/dX = −sin(X/R) and dx2/dX = cos(X/R) we have the Pythagorean identity (dx1)2 + (dx2)2 = (dX)2. The length of this cylindrical space is 2πR. |
|
|
|
We can form the Cartesian product of n such cylindrical spaces, with radii R1, R2, ..,Rn respectively, to give an n-dimensional space that is cylindrical in all directions, with a total "volume" of |
|
|
|
|
|
|
|
For example, a three-dimensional space that is everywhere locally Euclidean and yet cylindrical in all directions can be constructed by embedding the three spatial dimensions in a six-dimensional space according to the parameterization |
|
|
|
|
|
|
|
so the spatial Euclidean line element is |
|
|
|
|
|
|
|
giving a Euclidean spatial metric in a closed three-space with total volume (2π)3R1R2R3. Subtracting from this an ordinary temporal component gives an everywhere-locally-Lorentzian spacetime that is cylindrical in the three spatial directions, i.e., |
|
|
|
|
|
|
|
However, this last step seems half-hearted. We can imagine a universe cylindrical in all directions, temporal as well as spatial, by embedding the entire four-dimensional spacetime in a manifold of eight dimensions, two of which are purely imaginary, as follows: |
|
|
|
|
|
|
|
This leads again to the locally Lorentzian four-dimensional metric (1), but now all four of the dimensions X,Y,Z,T are periodic. So here we have an everywhere-locally-Lorentzian manifold that is closed and unbounded in every spatial and temporal direction. Obviously this manifold contains closed time-like worldlines, although they circumnavigate the entire universe. Whether such a universe would appear (locally) to possess a directional causal structure is unclear. |
|
|
|
We might imagine that a flat, closed, unbounded universe of this type would tend to collapse if it contained any matter, unless a non-zero cosmological constant is assumed. However, it's not clear what "collapse" would mean in this context. For example, it might mean that the Rn parameters would shrink, but they are not strictly dynamical parameters of the model. The four-dimensional field equations of general relativity operate only on X,Y,Z,T, so we have no context within which the Rn parameters could "evolve". Any "change" in Rn would imply some meta-time parameter τ, so that all the Rn coefficients in the embedding formulas would actually be functions Rn(τ). |
|
|
|
Interestingly, the local flatness of the cylindrical four-dimensional spacetime is independent of the value of R(τ), so if our "internal" field equations are satisfied for one set of Rn values they would be satisfied for any other values. The meta-time τ and associated meta-dynamics would be independent of the internal time T for a given observer unless we imagine some "meta field equations" relating τ to the internal parameters X,Y,Z,T. We might even speculate that these meta-equations would allow (require?) the values of Rn to be "increasing" versus τ, and therefore indirectly versus our internal time T = f(τ), in order to ensure stability. (One interesting question raised by these considerations of locally flat n-dimensional spaces embedded in flat 2n-dimensional spaces is whether every orthogonal basis in the n-space maps to an orthogonal basis in the 2n-space according to a set of formulas formally the same as those shown above, and, if not, whether there is a more general mapping that applies to all bases.) |
|
|
|
The above totally-cylindrical spacetime has a natural expression in terms of "octonion space", i.e., the Cayley algebra whose elements are two ordered quaternions |
|
|
|
|
|
|
|
Thus each point (X,Y,Z,T) in four-dimensional spacetime represents two quaternions |
|
|
|
|
|
|
|
To determine the absolute distances in this eight-dimensional manifold we again consider the eight coordinate differentials, exemplified by |
|
|
|
|
|
|
|
(using the rule for total differentials) so the squared differentials are exemplified by |
|
|
|
|
|
|
|
Adding up the eight squared differentials to give the square of the absolute differential interval leads again to the locally Lorentzian four-dimensional metric |
|
|
|
|
|
|
|
Naturally it isn't necessary to imagine an embedding of our hypothesized closed dimensions in a higher-dimensional space, but it can be helpful for visualizing the structure. One of the first suggestions for closed cylindrical dimensions was made by Theodor Kaluza in 1919, in a paper communicated to the Prussian Academy by Einstein in 1921. The idea proposed by Kaluza was to generalize relativity from four to five dimensions. The introduction of the fifth dimension increases the number of components of the Riemann metric tensor, and it was hoped that some of this additional structure would represent the electromagnetic field on an equal footing with the gravitational field on the "left side" of Einstein's field equations, instead of being lumped into the stress-energy tensor Tμν. Kaluza showed that, at least in the weak field limit for low velocities, we can arrange for a five dimensional manifold with one cylindrical dimension such that geodesic paths correspond to the paths of charged particles under the combined influence of gravitational and electromagnetic fields. In 1926 Oskar Klein proved that the result was valid even without the restriction to weak fields and low velocities. |
|
|
|
The fifth dimension seems to have been mainly a mathematical device for Kaluza, with little physical significance, but subsequent researchers have sought to treat it as a real physical dimension, and more recent "grand unification theories" have postulated field theories in various numbers of dimensions greater than four (though none with fewer than four, so far as I know). In addition to increasing the amount of mathematical structure, which might enable the incorporation of the electromagnetic and other fields, many researchers (including Einstein and Bergmann in the 1930's) hoped the indeterminacy of quantum phenomena might be simply the result of describing a five-dimensional world in terms of four-dimensional laws. Perhaps by re-writing the laws in the full five dimensions quantum mechanics could, after all, be explained by a classical field theory. Alas, as Bergmann later noted, "it appears these high hopes were unjustified". |
|
|
|
Nevertheless, theorists ever since have freely availed themselves of whatever number of dimensions seemed convenient in their efforts to devise a fundamental "theory of everything". In nearly all cases the extra dimensions are spatial and assumed to be closed with extremely small radii in terms of macroscopic scales, thus explaining why it appears that macroscopic objects exist in just three spatial dimensions. Oddly enough, it is seldom mentioned that we do, in fact, have six extrinsic relational degrees of freedom, consisting of the three open translational dimensions and the closed orientational dimensions, which can be parameterized (for example) by the Euler angles of a frame. These three dimensions are not individually cylindrical, nor do they commute, but at each point in three-dimensional space they constitute a closed three-dimensional manifold isomorphic to the group of rotations. It's also worth noting that while translational velocity in the open dimensions is purely relativistic, angular velocity in the closed dimensions is absolute, and there is no physical difficulty in discerning a state of absolute non-rotation. This is interesting because, even though a closed cylindrical space may be locally Lorentzian, it is globally absolute, in the sense that there is a globally distinguished state of motion with respect to which an inertial observer's natural surfaces of simultaneity are globally coherent. In any other state of motion the surfaces of simultaneity are helical in time, similar to the analytically continued systems of reference of observers at rest on the perimeter of a rotating disk. |
|
|
|
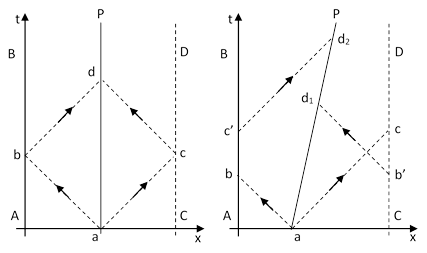
To illustrate, consider two possible worldlines of a single particle P in a one-dimensional cylindrical space as shown in the spacetime diagrams below. |
|
|
|
|
|
|
|
The cylindrical topology of the space is represented by identifying the worldline AB with the worldline CD. Now, in the left-hand figure the particle P is stationary, and it emits pulses of light in both directions at event a. The rightward-going pulse passes through event c, which is the same as event b, and then it proceeds from b to d. Likewise the leftward-going pulse goes from a to b and then from c to d. Thus both pulses arrive back at the particle P simultaneously. However, if the particle P is in absolute motion as shown in the right-hand figure, the rightward light pulse goes from a to c and then from cí to d2, whereas the leftward pulse goes from a to b and then from bí to d1, so in this case the pulses do not arrive back at particle P simultaneously. The absolutely stationary worldlines in this cylindrical space are those for which the diverging-converging light cones remain coherent. (In the one-dimensional case there are discrete absolute speeds greater than zero for which the leftward and rightward pulses periodically re-converge on the particle P.) |
|
|
|
Naturally for a different mapping between the events on the line AB and the events on the line CD we would get a different state of rest. The worldlines of identifiable inertial entities establish the correct mapping. If we relinquish the identifiability of persistent entities, both through time and under completed loops around the cylindrical dimension, then the mapping becomes ambiguous. For example, we assume particle P associates the pulses absorbed at event d with the pulses emitted at event a, although this association is not logically necessary. |
|
|