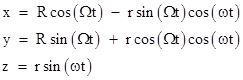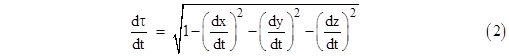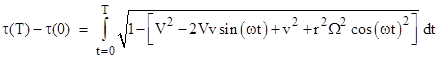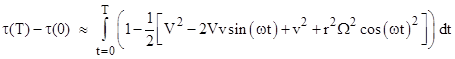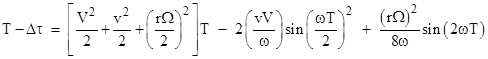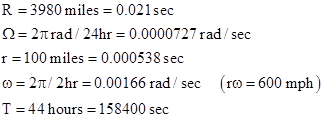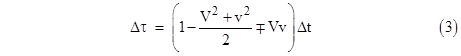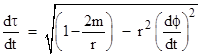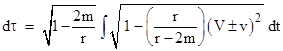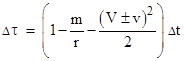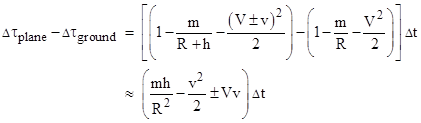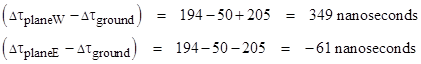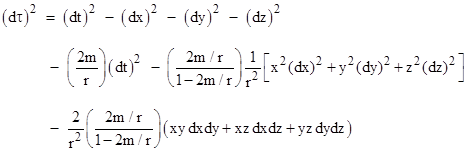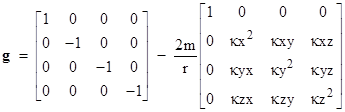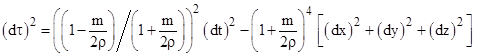6.6  Ideal Clocks in Arbitrary Motion

What is a clock? By a clock we understand any thing characterized by a phenomeon passing periodically through identical phases so that we must assume, by the principle of sufficient reason, that all that happens in a given period is identical with all that happens in any arbitrary period.

                                                                                      Albert Einstein, 1910

In his 1905 paper on the electrodynamics of moving bodies, Einstein noted that the Lorentz transformation has a “peculiar consequence”, namely, the elapsed time on an ideal clock as it proceeds from one given event to another depends on the path followed by that clock between those two events. The maximum elapsed time between two given events (in flat spacetime) applies to a clock that proceeds inertially between those events, whereas clocks that follow any other path will exhibit a lesser elapsed time. He expressed this as follows

If at the points A and B there are stationary clocks which, viewed in the resting system, are synchronous; and if the clock at A is moved with the velocity v along the line AB to B, then on its arrival at B the two clocks no longer synchronize, but the clock moved from A to B lags behind the other which has remained at B… It is at once apparent that this result still holds good if the clock moves from A to B in any polygonal line, and also when the points A and B coincide. If we assume that the result proved for a polygonal line is also valid for a continuously curved line, we obtain the theorem: If one of two synchronous clocks at A is moved in a closed curve with constant velocity until it returns to A… then the clock that moved runs slower than the one that remained at rest. Thus we conclude that a balance-clock at the equator must go more slowly… than a precisely similar clock situated at one of the poles under otherwise identical conditions.

The qualifying words “under otherwise identical conditions”, as well as the context, make it clear that the clocks are to be situated at the same gravitational potential – which will not be the case if they are both located at sea level (because the Earth’s rotation causes it to bulge at the equator by just the amount necessary to cause clocks at sea level to run at the same rate). This complication has sometimes caused people to claim that Einstein’s assertion about polar and equatorial clocks was in error, but at worst it just unnecessarily introduced an extraneous factor.

A more serious point of criticism of the above passage was partially addressed by a footnote added by Sommerfeld to the 1913 re-printing of Einstein’s paper. This pertains to the term “balance clock”, about which Sommerfeld said “Not a pendulum clock, which is physically a system to which the earth belongs. This case had to be excluded.” This reinforces the point that we are to exclude any differential effects of the earth’s gravitation, but it leaves unanswered the deeper question of what precisely constitutes a suitable “clock” for purposes of quantifying the elapsed proper time along any path. Some critics have claimed that Einstein’s assertion about time dilation involves circular reasoning, arguing that if any particular clock (or physical process) should fail to conform to the assertion, it would simply be deemed an unsuitable clock. Of course, ultimately all physical assertions involve this kind of circularity of definition, but the value of an assertion and definition depends not on its truth but on its applicability. If no physical phenomena were found to conform to the definition of proper time, then the assertion would indeed be worthless, but experience shows that the advance of the quantum wave function of any physical system moving from the event with coordinates x,y,z,t (in terms of an inertial coordinate system) to the event x+dx, y+dy, z+dz, t+dt is invariably in proportion to dτ where

Nevertheless, it can be argued that Einstein was not in a position to know this in 1905, because observations of the decay rates of sub-atomic particles (for example) under conditions of extreme acceleration had not yet been made. Miller has commented that Einstein’s “extension to the case where [the clock’s] trajectory was a continuous curve was unwarranted in 1905, but perhaps he considered that this case could always be treated as the limiting case of a many-sided polygon”. It should be noted, though, that Einstein carefully prefaced this “extension” with the words “if we assume”, so he can hardly be accused of smuggling. Also, as many others have pointed out, this “assumption” (the so-called “clock hypothesis”) can simply be taken as the definition of an ideal clock, and we are quite justified in expecting any real system with a periodic process to conform to this definition provided the restoring forces involved in the process are much greater than the inertial forces due to the acceleration of the overall system. Whether this kind of mechanistic assessment can be applied to the decay rates of sub-atomic particles is less clear. If for some extreme acceleration the decay rates of sub-atomic particles were found to differ from dτ given by (1), would we conclude that the Minkowski structure of spacetime was falsified, or that we had reached a level of acceleration that affects the decay process? Presumably if (1) broke down at the same point for a wide variety of processes, we would interpret this as the failure of Lorentz covariance, but if various processes begin to violate (1) at different levels of acceleration, we would be more likely to interpret those violations as being characteristics of the respective processes.

From the rationalist point of view, proper time can be conceived as independent of acceleration precisely because we can sense acceleration and correct for its effect, just as we can sense and correct for temperature, pressure, humidity, and so on. In contrast, we cannot sense velocity in any intrinsic way, so a purely local intrinsic clock cannot be corrected for velocity. Our notion of true time seems to be based on the idea of a characteristic periodic process under standard reference conditions, and then any intrinsically sensible changes in conditions are abstracted away. But even this notion involves idealizations, because (for example) there do not appear to be any perfectly periodic isolated processes. An ordinary clock is not in exactly the same state after each cycle of the escapement mechanism, because the driving spring has slightly relaxed. We regard the clock as essentially periodic because of the demonstrated insensitivity of the periodic components to the secular changes in the non-periodic components.

It’s possible to conceive of paradoxical “clocks”, such as a container of cooled gas, whose gradual increase in temperature (up to the ambient temperature) is used to indicate the passage of time. If we have two such containers, initially cooled to the same temperature, and then send one on a high speed journey in a spaceship with the same ambient temperature, we expect to find that the traveling container will be cooler than the stationary container when they are re-united. Furthermore, if the gas consisted of radioactive particles, we expect less decay in the gas in the traveling container. However, this applies only because we accelerated the gas molecules coherently. Another way of increasing the velocities of the molecules in a container is by applying a separate heat source. Obviously this has the effect of “speeding up” the time as indicated by the temperature rise, but it slows down the radio-active decay of those molecules. This is just a simple illustration of how the rate of progression of a macroscopic system toward thermodynamic equilibrium may be affected in the opposite sense as the rate of quantum decay of the elementary particles comprising that system. The key to maintaining a consistent proper time for macroscopic as well as microscopic processes seems to be coherent acceleration (work) as opposed to incoherent acceleration (heat).

In the preceding sections we've looked at circular and radial free-falling paths in a spherically symmetrical gravitational field, but many circumstances involve more complicated paths, including acceleration. For example, suppose we place highly accurate cesium clocks in an airplane and fly it around in a circle with a 100 mile radius above an airport on the equator. Assume that for the duration of the experiment the Earth has uniform translational velocity and rotates once per 24 hours. In terms of an inertial coordinate system whose origin is at the center of the Earth, the coordinates of the plane are

where R is the radius of the Earth plus the height of the airplane above the Earth's surface, Ω is the Earth's rotational speed, r is the radius of the circular flight path, and ω is the airplane's angular speed. Differentiating these inertial coordinates with respect to the coordinate time t gives expressions for dx/dt, dy/dt, and dz/dt. Now, the proper time of the clock is given by the integral of dτ over its worldline. Neglecting (for the moment) the effect of the Earth's gravitational field, we can divide through equation (1) by (dt)² and take the square root to give

Therefore, if we let V and v denote the speeds RΩ and rω respectively, the elapsed proper time for the clock corresponding to T of inertial coordinate time is given exactly by the integral

Since all the dimensionless parameters V, v, rΩ are extremely small compared to 1, we can approximate the square root very closely using  ≈ 1 − u/2, which gives the easily integrable expression

Subtracting the result from T gives the amount of dilation for the path in question. The result is

Only the first on the right is multiplied by T, so it represents the secular contributions to the time dilation, i.e., the parts that grow in proportion to the total elapsed time, whereas the two right hand terms are cyclical and don't accumulate as T increases. Not surprisingly, if we set v = r = 0 the amount of dilation is simply V²T/2, which is the dilation for the fixed point at the airplane's height above the equator, due entirely to the Earth's rotation. On the other hand, if we take the following values

we find that the clock fixed at a point on the equator runs slow by 100.69 nsec per 24 hours relative to our Earth-centered inertial coordinate system, whereas a clock going around in a circle of radius 100 miles at 600 mph would lose 134.99 nsec per 24 hours (neglecting the cyclical components).

Another experiment that could be performed is to fly clocks completely around the Earth's equator in opposite directions, so the eastbound clock's flight speed v (relative to the ground) would be added to the circumferential speed V of the Earth's surface due to the Earth's rotation, whereas the westbound clock's flight speed v would be subtracted. In this situation the spatial coordinates of the clocks in the equatorial plane would be given by

where we take the + sign for the eastbound plane and – for the westbound plane. This gives the derivatives

Substituting into equation (2) and simplifying gives

Multiplying through by dt and integrating from t = 0 to some arbitrary coordinate time Δt, we find that the corresponding lapse of proper time for the plane is

It follows that the lapse of time on the westbound clock by any coordinate time Δt will exceed the lapse of time on the eastbound clock by 2(Δt)Vv.

To this point we have neglected the gravitational field of the Earth by assuming that the metric of spacetime was the flat Minkowski metric. To account for the effects of gravity we should really use the Schwarzschild metric (assuming a spherical Earth). We saw in Section 6.4 that the metric in the equatorial plane of a spherical gravitating body of mass m at a constant Schwarzschild radial parameter r from the center of that body is

where τ is the proper time along the path, t is the coordinate time, and ϕ is the longitude. Dividing through by (dt)² and taking the square root of both sides gives

Let R denote the "radius" of the Earth, and let r = R + h denote the radius of the airplane's flight path at the constant altitude h. If we again let V denote the tangential speed of the Earth's rotation at the airplane's radial position at the equator, and let v denote the tangential speed of the airplane (either eastward or westward), we have dϕ/dt = (V±v)/r, so the above equation leads to the integral for the elapsed proper time along a path in the equatorial plane at radial parameter r = R+h from the Earth's center and with a tangential speed (relative to a fixed position above a point on the Earth's surface) is

Again making use of the approximation ≈ 1 − u/2 for small u, we can integrate this over some interval Δt of coordinate time to give (to the first order) the corresponding lapse Δτ of proper time along the path

Naturally this is the same as equation (3) except for the extra term –m/r, which represents the effect of the gravitational field. The difference in elapsed times between a clock at rest on the ground at the equator and a clock in an airplane at height h above the ground moving east or west along the equator at speed v is therefore

The mass of the Earth in gravitational units is about m = 0.0044 meters. Assume the airplanes are flying at an altitude of h = 10000 meters (about 35000 ft) above the Earth's surface, which has a radius of R = (6.378)10⁶ meters. Also, assume the speed of the airplanes (relative to the ground) is v = 500 mph, which is v = (0.747)10⁻⁶ in dimensionless units, compared with the tangential speed of the Earth's surface at the equator V = (1.527)10⁻⁶. In these conditions the clocks will circumnavigate the Earth in about Δt = 50 hours. The first term in the above formula, representing the gravitational effect, is about 194 nanoseconds, and the second term subtracts about 50 nanoseconds. The third term adds about 205 nanoseconds for the westbound clock, and subtracts that amount for the eastbound clock. This gives the overall results

Note that, in terms of the Earth-centered inertial coordinates, the eastbound clock has the greatest speed, the ground based clock has the middle speed, and the westbound clock has the lowest speed, so the latter shows the greatest elapsed time.

These effects are extremely small, but they are measureable with with modern atomic clocks. Cesium clocks can achieve accuracy of 2 nanoseconds per day, and other more advanced clocks are even more precise. Experiments of this type have actually been performed on airplanes circumnavigating the globe (though not at the equator), and the results have agreed with the predictions of relativity. The best current clocks are reportedly capable of detecting the gravitational time dilation for changes in elevation of just half a meter, and for speeds of just 20 miles per hour.

Suppose we return to our original problem, which involved airplanes flying in a small circle around a fixed point on the Earth's equator, but now we want to include the effects of the Earth's gravity. The principles are the same as in the circumnavigating case, i.e., we need only integrate the proper time along the path, making use of the Schwarzschild metric to give the correct line element. However, the path of the airplane in this case is not so easy to express in terms of the usual Schwarzschild polar coordinates. One way of approaching a problem such as this is to work with the Schwarzschild metric expressed in terms of "orthogonal" quasi-Minkowskian coordinates. If we split up the coefficient of (dr)² into the form 1 + 2m/(r–2m), then the usual Schwarzschild metric can be written as

Now if we define the quasi-Euclidean parameters

we recognize the last three terms of the preceding equation as just the expression of (dx)² + (dy)² + (dz)² in polar coordinates. Also, since r² = x² + y² + z², we have dr = (xdx + ydy + zdz)/r, so the Schwarzschild metric can be written in the quasi-Minkowskian form

This form is similar to Riemann normal coordinates if we expand this metric about any radius r. Also, for sufficiently large r the quantity 2m in the denominator of the final term becomes negligible, and the coefficient approaches –2m/r³, so it isn't surprising that this is one of the characteristic magnitudes of the sectional curvature of Schwarzschild spacetime at radius r. Expanding the above expression, we find that the Schwarzschild metric can be expressed as a sum of the Minkowski metric plus some small quantities as shown below

Thus in matrix notation the Schwarzschild metric tensor for these coordinates is

where κ = 1 / [r²(1 – 2m/r)]. The determinant of this metric is –1. Dividing the preceding expression by (dt)² and taking the square root of both sides, we arrive at a relation between dt and dτ into which we can substitute the expressions for x,y,z, r, dx/dt, dy/dt, and dz/dt, and then integrate to give the proper time Δτ along the path as a function of coordinate time Δt. Hence if we know x,y, and z as explicit functions of t along a particular path, we can immediately write down the explicit integral for the lapse of proper time along that path.

The above discussion was expressed in terms of quasi-Euclidean coordinates based on the Schwarzschild radial coordinate r in accord with (4), but if we replace r in (4) with the radial coordinate ρ of isotropic coordinates (see the end of Section 8.4) the line element is

which to lowest order in m/ρ is (1 – 2m/ρ)(dt)² – (1 + 2m/ρ)[(dx)² + (dy)² + (dz)²].

Return to Table of Contents