6.1  An Exact Solution

Einstein had been so preoccupied with other studies that he had not realized such confirmation of his early theories had become an everyday affair in the physical laboratory. He grinned like a small boy, and kept saying over and over “Ist das wirklich so?”

                                                                    A. E. Condon

The special theory of relativity posits the existence of a unique class of global coordinate systems - called inertial coordinates - with respect to which inertia is homogeneous and isotropic. It was natural, then, to express physical laws in terms of this preferred class of coordinate systems. The special theory also strongly suggested the fundamental equivalence of mass and energy, according to which light – and every other form of energy – must be regarded as possessing inertia. It follows that the speed of light in vacuum has an invariant value, c, in all directions in terms of any inertial coordinate system. However, it soon became clear that the existence of global inertial coordinate systems (with invariant light speed) together with the idea that energy has inertia (as expressed in the famous relation E² = m² + |p|²) were incompatible with one of the most firmly established empirical results of physics, namely, the exact proportionality of inertial and gravitational mass. The latter implies that a pulse of light must be deflected in a gravitational field, which clearly requires the wavefront to have different speeds at different locations in terms of suitable global coordinates. This incompatibility led Einstein, as early as 1907, to the belief that the premise of global inertial coordinate systems could not be maintained. We can establish inertial coordinates over any sufficiently small region of space and time, but there do not exist any global systems of inertial coordinates in regions where gravitating mass-energy is present.

Since no preferred class of global coordinate systems exists, the general theory essentially places all (smoothly related) systems of coordinates on an equal footing, and expresses physical laws in a way that is applicable to any of these systems. As a result, the laws of physics will hold good even with respect to coordinate systems in which the speed of light takes on values other than c. For example, the laws of general relativity are applicable to a system of coordinates that is fixed rigidly to the rotating Earth. According to these coordinates the distant galaxies are "circumnavigating" nearly the entire universe in just 24 hours, so their speed is obviously far greater than the constant c. The huge implied velocities of the celestial spheres was always problematical for the ancient conception of an immovable Earth, but it is beautifully accommodated within general relativity, in which any “fictitious forces” that arise in accelerating coordinates affect the values of the metric components g_uv for those coordinates. When expressed in a rotating system of coordinates, the distant stars are indeed moving with dx/dt values that far exceed the usual numerical value of c, but they are not moving faster than light, because the speed of light at those locations, expressed in terms of those coordinates, is correspondingly greater.

In general, for any given system of coordinates the velocity of light can always be inferred from the components of the metric tensor, and typically looks something like 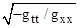. To understand this, recall that in special relativity we have global inertial coordinate systems such that the metric tensor has the constant form

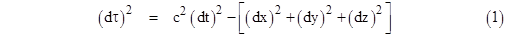
The trajectory of a light ray follows a null path, i.e., a path with dτ = 0, so dividing by (dt)² we see that the path of light everywhere satisfies the equation

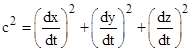
Hence the velocity of light is unambiguous in terms of these preferred systems of coordinates. However, in the general theory we are no longer guaranteed the existence of a global coordinate system with a constant metric of the simple form (1). It is true that over a sufficiently small spatial and temporal region surrounding any given event in spacetime there exists a coordinate system of that simple Minkowskian form, but in the presence of a non-vanishing gravitational field ("curvature") equation (1) applies only with respect to "free-falling" inertial coordinates, which are necessarily transient and don't extend globally.

So, for an extended region of spacetime, instead of writing the metric in the xt plane as (dτ)² = (dt)² – (dx)² , we must consider the more general form

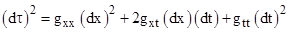
where the coefficients are functions of the coordinates. As always, the path of a light ray is null, so dτ = 0 and the differentials dx and dt satisfy the equation

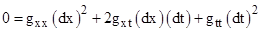
Solving this gives

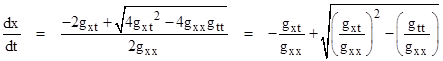
If we diagonalize our metric we get g_xt = 0, in which case the "velocity" of a null path in the xt plane with respect to this coordinate system is simply dx/dt = 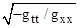. This quantity can (and does) take on any value, depending on our choice of coordinate systems.

Around 1911 Einstein proposed to incorporate gravitation into a modified version of special relativity by allowing the speed of light to vary as a scalar from place to place in Euclidean space as a function of the gravitational potential. This "scalar c field" is remarkably similar to a simple refractive medium, in which the speed of light varies as a function of the density. Fermat's principle of least time can then be applied to define the paths of light rays as geodesics in the spacetime manifold (as discussed in Section 8.4). Specifically, Einstein wrote in 1911 that the speed of light at a place with the gravitational potential φ would be c₀ (1 + φ/c₀²), where c₀ is the nominal speed of light in the absence of gravity. In geometrical units we define c₀ = 1, so Einstein's 1911 formula can be written simply as c = 1 + φ. However, this formula for the speed of light – indeed, this whole approach to gravity – turned out to be incorrect. In the general theory of relativity, completed in 1915, the speed of light in a gravitational field cannot generally be represented by a simple scalar field of c values in Euclidean space, due to the intrinsic curvature of spacetime. In terms of some quite natural coordinate systems, the speed of light varies not only from place to place, but also in different directions at any given place (even though the speed of light always has the invariant value c in terms of local free-falling inertial coordinates, consistent with the equivalence principle). For example, near a spherically symmetrical and non- rotating mass, we can define stationary coordinates in which the speed of light is isotropic, but in these coordinates the circumference of a circular orbit of radius r is not equal to 2πr. On the other hand, we can define stationary coordinates in which a circular orbit of radius r does equal 2πr, but in terms of these coordinates the circumferential speed of light differs from the radial speed. The former is given by the same formula as in Einstein’s 1911 paper, but the latter differs from the 1911 formula by a factor of 2 on the “potential” term. To explain this in detail, we must first consider how the Schwarzschild metric is derived from the field equations of general relativity.

To deduce the implications of the field equations for observable phenomena Einstein originally made use of approximate methods, since no exact solutions were known. These approximate methods were adequate to demonstrate that the field equations lead in the first approximation to Newton's laws, and in the second approximation to a natural explanation for the anomalous precession of Mercury (see Section 6.2). However, these results can now be directly computed from the exact solution for a spherically symmetric field, found by Karl Schwarzschild in 1916. As Schwarzschild wrote, it's always pleasant to find exact solutions, and the simple spherically symmetrical line element "let's Mr. Einstein's result shine with increased clarity". To this day, most of the empirically observable predictions of general relativity are consequences of this simple solution.

We will discuss Schwarzschild's original derivation in Section 8.7, but for our present purposes we will take a slightly different approach. Recall from Section 5.5 that the most general form of the metrical spacetime line element for a spherically symmetrical static field (although it is not strictly necessary to assume the field is static) can be written in polar coordinates as

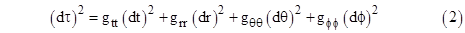
where g_θθ = –r², g_ϕϕ = –r² sin(θ)², and g_tt and g_rr are functions of r and the gravitating mass m. (These stipulations ensure that the circumference of a circular orbit of radius r is 2πr.) We expect that if m = 0, and/or as r increases to infinity, we will have g_tt = 1 and g_rr = –1 in order to give the flat Minkowski metric in the absence of gravity. We saw in Section 5.5 that in this highly symmetrical context there is a fairly plausible way to derive the metric coefficients g_tt and g_rr simply from the requirement to satisfy Kepler's third law and the inverse-square law, but with some ambiguity over the choice between proper time and coordinate time. We can now determine unambiguously the values of these metric coefficients consistent with Einstein's field equations.

In any region that is free of (non-gravitational) mass-energy the vacuum field equations must apply, which means the Ricci tensor

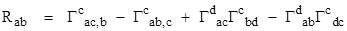
must vanish, i.e., all the components are zero. Since our metric is in diagonal form, it's easy to see that the Christoffel symbols for any three distinct indices a,b,c reduce to

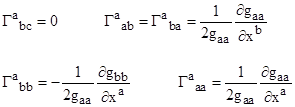
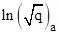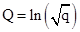with no summations implied. In two of the non-vanishing cases the Christoffel symbols are of the form q_a/(2q), where q is a particular metric component and subscripts denote partial differentiation with respect to x^a. By an elementary identity these can also be written as . Hence if we define the new variable  we can write the Christoffel symbol in the form Q_a with q = e^2Q. Accordingly if we define the variables (functions of r)

then we have

and the non-vanishing Christoffel symbols (as given in Section 5.5) can be written as

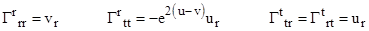
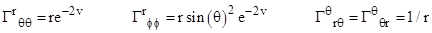
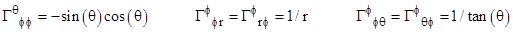
We can now write down the components of the Ricci tensor, each of which must vanish in order for the field equations to be satisfied. Writing them out explicitly and expanding all the implied summations for our line element, we find that all the non-diagonal components are identically zero (which we might have expected from symmetry arguments), so the only components of interest in our case are the diagonal elements

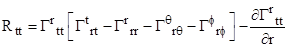
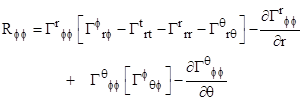
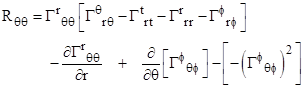
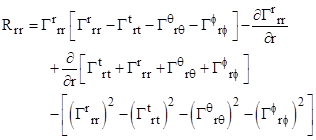
Inserting the expressions for the Christoffel symbols gives the equations for the four diagonal components of the Ricci tensor as functions of u and v:

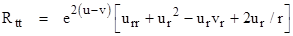
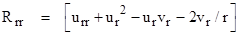
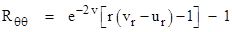
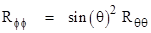
The necessary and sufficient condition for the field equations to be satisfied by a line element of the form (2) is that these four quantities each vanish. Combining the expressions for R_tt and R_rr we immediately have u_r = –v_r , which implies u = –v + k for some arbitrary constant k. Making these substitutions into the equation for R_θθ we get the condition

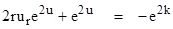
Remembering that e^2u = g_tt, and that the derivative of e^2u is 2u_r e^2u, this condition expresses the requirement

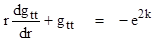
The left side is just the chain rule for the derivative of the product rg_tt, and since this derivative equals the constant –e^2k we immediately have rg_tt = –e^2kr + α for some constant α, and hence g_tt = –e^2k + α/r. As r increases to infinity the metric must go over to the Minkowski metric, which has g_tt = 1, so we must have –e^2k = 1, which implies that k = πi/2. Also, since g_rr = e^2v where v = –u + πi/2, it follows that g_rr = –1/g_tt, and so we have the results

To match the Newtonian limit we set a = –2m where m is classically identified with the mass of the gravitating body. These metric coefficients were derived by combining the expressions for R_tt and R_rr, but it's easy to verify that they also satisfy each of those equations separately. Thus, substituting these expressions into the line element (2), we arrive at the essentially unique (up to changes in coordinate systems) spherically symmetrical static solution of Einstein's field equations

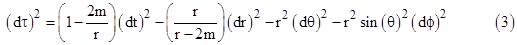
Now that we have derived the Schwarzschild metric, we can easily correct the "speed of light" formula that Einstein gave in 1911. A ray of light always travels along a null trajectory, i.e., with dτ = 0, and for a radial ray we have dθ and dϕ both equal to zero, so the equation for the light ray trajectory through spacetime, in Schwarzschild coordinates (which are essentially the only spherically symmetrical ones in which the metric is independent of t and the circumference of a circle of radius r is 2πr) is simply

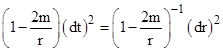
from which we get

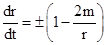
where the ± sign just indicates that the light can be going radially inward or outward. (We're using geometric units, so c = G = 1.) In the Newtonian limit the classical gravitational potential at a distance r from mass m is φ = –m/r, so if we let c_r = dr/dt denote the radial speed of light in Schwarzschild coordinates, we have

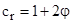
which corresponds to Einstein's 1911 equation, except that we have a factor of 2 instead of 1 on the potential term. Thus, as φ becomes increasingly negative (i.e., as the magnitude of the potential increases), the radial "speed of light" c_r defined in terms of the Schwarzschild parameters t and r is reduced to less than the nominal value of c. The factor of 2 relative to the equation of 1911 arises because in the full theory there is gravitational length contraction as well as time dilation. The length contraction doesn’t affect the gravitational redshift, which is purely a function of the time dilation, so the redshift prediction of 1911 remains valid. Only the radial speed of light (in terms of Schwarzschild coordinates) is changed.

On the other hand, if we define the tangential speed of light at a distance r from a gravitating mass center in the equatorial plane (θ = π/2) in terms of the Schwarzschild coordinates as c_t = r(dϕ/dt), then the metric divided by (dt)² immediately gives

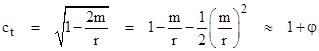
Thus, we again find that the "velocity of light" is reduced a region with a strong gravitational field, but this speed is the square root of the radial speed at the same point, and to the first order in m/r this is the same as Einstein's 1911 formula, although it is understood now to signify just the tangential speed. This illustrates the fact that the general theory doesn't lead to a simple scalar field of c values in Euclidean space. The effects of gravitation can only be accurately represented by a tensor field. (It’s possible to define so-called isotropic coordinates, as discussed in Section 8.4, in terms of which the speed of light is the same in all directions, but only by using a radial coordinate in terms of which the circumference of a circular orbit of radius r is not 2πr, which shows the non-Euclidean character of the space.)

As mentioned, one of the observable implications of general relativity (as well as any other metrical theory that respects the equivalence principle) is gravitational redshift, which is a consequence of the fact that, for any stationary metric, the rate of proper time at a fixed radial position in a gravitational field relative to the coordinate time is given by

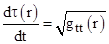
Since the coordinate time for successive wavecrests to traverse a fixed interval is the same, the characteristic frequency ν₁ of light emitted by some known physical process at a radial location r₁ will represent a different frequency ν₂ with respect to the proper time at some other radial location r₂ according to the formula

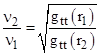
From the Schwarzschild metric we have g_tt(r_j) = 1+2φ_j where φ_j = –m/r_j is the gravitational potential at r_j, so

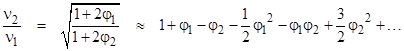
Neglecting the higher-order terms and rearranging, this can also be written as

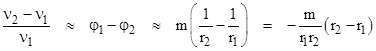
Observations of the light emitted from the surface of the Sun, and from other stars, is consistent with this predicted amount of gravitational redshift (up to first order), although measurements of this slight effect are difficult. A terrestrial experiment performed by Rebka and Pound in 1960 exploited the Mossbauer effect to precisely determine the redshift between the top and bottom of a tower. The results were in good agreement with the above formula, and subsequent experiments of the same kind have improved the accuracy to within about 1 percent. (Note that if r₁ and r₂ are nearly equal, as, for example, at two heights near the Earth's surface, then the leading factor of the right-most expression is essentially just the acceleration of gravity a = –m/r², and the factor in parentheses is the difference in heights Δh, so we have Δν/ν = a Δh.)

However, it's worth noting that this amount of gravitational redshift is a feature of just about any viable metrical theory of gravity that includes the equivalence principle (e.g., Nordstrom’s scalar theory), so these experimental results, although useful for validating that principle, are not very robust for distinguishing between competing theories of gravity. For this we need to consider other observations, such as the paths of light near a gravitating body, and the precise orbits of planets. These phenomena are discussed in the subsequent sections.

Return to Table of Contents