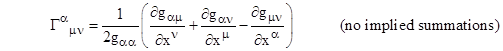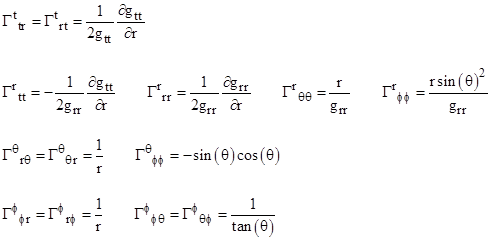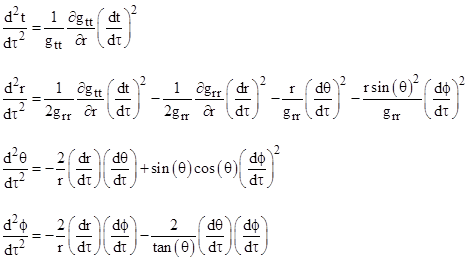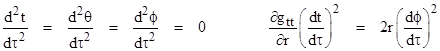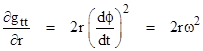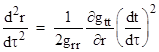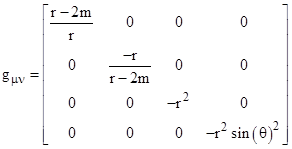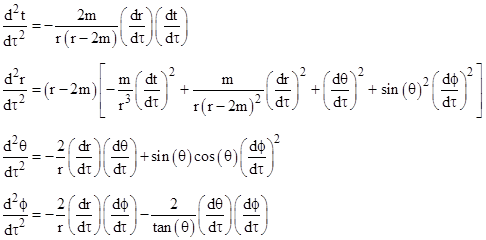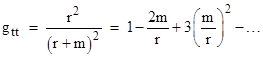5.5  Schwarzschild Metric From Kepler's 3rd Law

In that same year [1665] I began to think of gravity extending to the orb of the Moon & from Kepler’s rule of the periodical times of the Planets being in sesquialterate proportion of their distances from the centers of their Orbs, I deduced that the forces which keep the Planets in their Orbs must be reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the earth, and found them answer pretty nearly.

                                                                                                                   Isaac Newton

The simplest non-trivial configuration of spacetime in which gravity plays a role is for the region surrounding a static mass point, for which we can assume that the metric has perfect spherical symmetry and is independent of time. Historically this was first found by Karl Schwarzschild in 1916 as a solution of Einstein’s field equations (see Section 6.1), and all the original empirical tests of general relativity can be inferred from this solution. However, even without knowing the field equations of general relativity, it is possible to give a very plausible (if not entirely rigorous) derivation of the Schwarzschild metric purely from knowledge of the inverse square characteristic of gravity, Kepler’s third law for circular orbits, and the null intervals of light paths.

Let r denote the radial spatial coordinate, so that every point on a surface of constant r has the same intrinsic geometry and the same relation to the mass point, which we fix at r = 0. Also, let t denote our temporal coordinate. Any surface of constant r and t must possess the two-dimensional intrinsic geometry of a 2-sphere, and we can scale the radial parameter r such that the area of this surface is 4π r². (Notice that since the space may not be Euclidean, we don't claim that r is "the radial distance" from the mass point. Rather, at this stage r is simply an arbitrary radial coordinate scaled to give the familiar Euclidean surface area.) With this scaling, we can parameterize the two-dimensional surface at any given r (and t) by means of the ordinary "longitude and latitude" spherical metric

where dS is the incremental distance on the surface of an ordinary sphere of radius r corresponding to the incremental coordinate displacements dθ and dϕ. The coordinate θ represents "latitude", with θ = 0 at the north pole and θ = π/2 at the equator. The coordinate ϕ represents the longitude relative to some arbitrary meridian.

It follows that the complete spacetime metric near a spherically symmetrical mass m can be written in the diagonal form

where g_θθ = -r², g_ϕϕ = -r² sin(θ)², and g_tt and g_rr are (as yet) unknown functions of r and the central mass m. Of course, with m = 0 the functions g_tt and -g_rr must both equal 1 in order to give the flat Minkowski metric (in polar form), and we also expect that as r increases to infinity these functions both approach 1, regardless of m, since we expect the metric to approach flatness sufficiently far from the gravitating mass.

This metric is diagonal, so the non-zero components of the contravariant metric tensor are g^αα = 1/g_αα. In addition, the diagonality of the metric allows us to simplify the definition of the Christoffel symbols to

Now, the only non-zero partial derivatives of the metric coefficients are

along with ∂g_tt/dr and ∂g_rr/dr, which are yet to be determined. Inserting these values into the preceding equation, we find that the only non-zero Christoffel symbols are

As explained in Section 5.4, these are the coefficients of the four geodesic equations near a spherically symmetrical mass, i.e., the equations of paths for which the integrated path length is unchanged by incremental variations of the path. Writing them out in full, we have

In the absence of non-gravitational forces, we postulate that any test particle follows a geodesic path, so these equations characterize inertial/gravitational motions of test particles in a spherically symmetrical field. All that remains is to determine the metric coefficients g_tt and g_rr.

We expect that one possible solution should be circular Keplerian orbits, i.e., if we regard r as corresponding (at least approximately) to the Newtonian radial distance from the center of the mass, then there should be a circular geodesic path at constant r that revolves around the central mass m with an angular velocity of ω, and these quantities must be related (at least approximately) in accord with Kepler's third law

(The original deductions of an inverse-square law of gravitation by Hooke, Wren, Newton, and others were all based on this same empirical law. See Section 8.1 for a discussion of the origin of Kepler's law.) If we consider purely circular motion on the equatorial plane (θ = π/2) at constant r, the metric reduces to

and since dr/dτ = 0 the geodesic equations for these circular paths reduce to

Multiplying through by (dτ/dt)² and identifying the angular speed ω with the derivative of ϕ with respect to the coordinate time t, the right hand equation becomes

For consistency with Kepler's Third Law we must have ω² equal (or very nearly equal) to m/r³, so we make this substitution to give

Integrating this equation, we find that the metric coefficient g_tt must be of the form k - (2m/r) where k is a constant of integration. Since g_tt must equal 1 when m = 0 and/or as r approaches infinity, it's clear that k = 1, so we have

Also, for a photon moving away from the gravitating mass in the purely radial direction, we have dτ = 0, and so our basic metric for a purely radial ray of light gives

Next we consider a stationary test particle at a radial coordinate r. The metric equation gives the line element for the worldline of this test particle

and we also have the radial geodesic equation for this particle

The left hand side is the acceleration of gravity d²r/dτ² in geometrical units, which is taken to be the inverse square expression –m/r². Inserting this expression and substituting from equations (1) and (4), we get

This implies g_rr = -1/g_tt (corresponding to the “perpendicular” factorization g_tt = dr/dt and g_rr = -dt/dr in equation (3)), so we have the complete Schwarzschild metric

from which nearly all of the experimentally accessible consequences of general relativity follow.

In matrix form the Schwarzschild metric is written as

Now that we've determined g_tt and g_rr, we have the partials

so the Christoffel symbols that we previously left undetermined are

Therefore, the complete set of geodesic equations for the Schwarzschild metric are

In these equations we’ve taken the proper time τ as our path length parameter, which is suitable for massive particles that follow time-like paths. On the other hand, the lapse of proper time along the path of a massless pulse of energy (such as a photon) is zero by definition, so this raises an interesting question: How can we make stationary the “length” of a path whose length is identically zero? One approach is to evaluate the integrated equations of motion for timelike paths in the limit as dτ goes to zero, but for a metric whose coefficients are independent of coordinate time another approach is to set dτ = 0 in the basic metric and solve for the light-like geodesics by taking coordinate time as the path parameter, which leads to Fermat’s principle of least time as will be discussed in Sections 6.3 and 8.4.

To show that the equations of motion derived above correspond to those of Newtonian gravity in the weak slow limit, we need only note that if the speed dr/dτ is very small compared with the speed of light, the square of this speed will be negligibly small. Likewise in this limit the value of dt/dτ is essentially equal to 1, and it's easy to see that if the motion of a test particle is initially in the plane θ = π/2 then it remains always in that plane, and by spherical symmetry this applies to all planes. So we can assume θ = π/2 and with the stated approximations the equations of motion reduce to the familiar Newtonian equations

where ω is the angular velocity.

Despite this agreement, there is an undeniable ambiguity in the application of Kepler's third law and the inverse square law as heuristic guides to the equations of motion, due to the distinction between coordinate time t and proper time τ. Newtonian physics didn't distinguish between these two, which is not surprising, since the two are practically indistinguishable in weak gravitational fields for objects moving at much less than the speed of light. Nevertheless, the slight deviation between these two time parameters has observable consequences, and provides important tests for distinguishing between the spacetime geodesic approach and the Newtonian force-at-a-distance approach to gravitation. In our derivation we assumed that Kepler's third law is exactly satisfied with respect to coordinate time t rather than to the proper time τ of the orbiting particle, i.e., we defined the angular speed ω of the orbit as dϕ/dt rather than dϕ/dτ, whereas we assumed that the simple inverse-square acceleration law is satisfied with respect to the proper time τ of the falling particle. Thus, without some rationale for why Kepler’s law for circular orbits should have its simplest expression in terms of this particular coordinate time (i.e., the time coordinate in terms of which the metric is stationary) while the radial acceleration of a stationary particle should have its simplest expression in terms of proper time, the derivation is not free of ambiguity. In fact, had we assumed Kepler’s law applies in terms of proper time by defining ω as dϕ/dτ instead of dϕ/dt, we would have gotten

and the negative inverse of this for g_rr. These coefficients give the same Newtonian limit as the Schwarzschild metric, differing from the latter only in the second order of m/r, but their behavior is drastically different when m/r becomes large. For example, unlike the Schwarzschild metric coefficients, they do not exhibit a coordinate singularity at r = 2m. From an empirical standpoint, this alternative metric would give the same gravitational red shift and the same deflection of light as does general relativity, since those effects depend only on the first order terms. However, the precession of elliptical orbits depends on a second-order term in g_rr, and this alternative metric gives just one half of the correct value for the precession. (In terms of the “Robertson-Eddington” parameters this metric has α = γ = 1 and β = 5/2.) This shows the importance of the field equations for providing a sound basis for the metric – and it also shows the importance of orbital precession as a test to discriminate between alternative metrical theories of gravity.

Return to Table of Contents