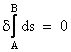4.6  The Field of All Fields

Classes and concepts may be conceived as real objects, existing independently of our definitions and constructions. It seems to me that the assumption of such objects is quite as legitimate as the assumption of physical bodies, and there is quite as much reason to believe in their existence.

                                                                                                                Kurt Gödel, 1944

Where is the boundary between the special and general theories of relativity? It is sometimes said that any invocation of "general covariance" implies general relativity, but just about any theory can be expressed in a generally covariant form, so this doesn't even distinguish general relativity from Newtonian physics, let alone from special relativity. For example, it's perfectly possible to transform the special relativistic solution of a rotating platform into some arbitrary accelerated coordinate system, and although the result is ugly, it is no less (or more) valid than when it was expressed in terms of non-accelerating coordinates, because the transformation from one stipulated set of coordinates to another has no physical content. But the key word there is "stipulated", because the special and general theories differ significantly in what they take for granted.

Special relativity is analogous to "naive set theory" in mathematics, in the sense that it is based on certain plausible-sounding premises which actually are quite serviceable for treating a wide class of problems, but which, on close examination, are susceptible to self-referential antinomies. This is most evident with regard to the assumption of the identifiability of inertial frames. As Einstein remarked, "in the special theory of relativity there is an inherent epistemological defect", namely, that the preferred class of reference frames on which the theory relies is circularly defined. Special relativity asserts that the lapse of proper time between two (timelike-separated) events is greatest along the inertial worldline connecting those two events - a seemingly interesting and useful assertion - but if we ask which of the infinitely many paths connecting those two events is the "inertial" one, we can only answer that it is the one with the greatest lapse of proper time, or with other attributes the ultimately reduce to the same thing. The definition of an inertial path from event A to event B through spacetime is based on the variational principle

according to which the proper time is stationary along the path. If we simply accept this uncritically, and are willing to naively rely on the testimony of accelerometers as unambiguous indicators of "inertia", we have a fairly solid basis on which to do physics, and we can certainly work out correct answers to many questions. However, the circularity in this procedure was worrisome to Einstein, since we can conclude that the path of an object is straight only if it is sufficiently unaffected by other objects, but we know it is sufficiently unaffected by other objects only based on whether its path is straight. This epistemological defect caused him (in a remarkably short time) to abandon special relativity and global Lorentz invariance as a suitable conceptual framework for the formulation of physics. More specifically, the naive reliance on accelerometers as unambiguous indicators of global inertia in the context of special relativity is immediately undermined by the equivalence principle, because we're then required to predicate any application of special relativity on the absence (or at least the negligibility) of irreducible gravitational fields, and this condition is simply not verifiable within special relativity itself, because of the circularity in the principle of inertia.

Given the recognized limitations of special relativity, and considering how successfully it was generalized and extended in 1915, we may wonder why it's even necessary to continue carrying along the special theory as a conceptually distinct entity. Will this duality persist indefinitely, or will we eventually just say there is a single theory of relativity (the theory traditionally called general relativity), which subsumes and extends the earlier theory called special relativity?  The reluctance to discard the special theory as a separate theory may be due largely to the fact that it represents a simple and widely- applicable special case of the general theory, and it's convenient to have a name for this limiting case. (There are, however, many situations in which the holistic approach of the general theory is actually much simpler than the traditional special-theory-plus-general-corrections approach.) Another reason that's sometimes mentioned is the (remote) possibility that Einstein's general relativity is not the "right" generalization/extension of the special theory. For example, if observation were ever to conclusively rule out the existence of gravitational waves (which is admittedly hard to imagine in view of the available binary star data), it might be necessary to seek another framework within which to place the special theory. In this sense, we might regard special relativity as roughly analogous to set theory without the axiom of choice, i.e., a restricted and less ambitious theory that avoids making use of potentially suspect concepts or premises.

However, it's hard to say exactly which of the fundamental principles of general relativity is considered to be suspect. We've seen that "general covariance" is a property of almost any theory, so that can't be a problem, although it also can’t be cited as giving unique support to general relativity, unless it’s combined with a criterion of simplicity or naturalness. We might doubt the equivalence principle in one or more of its various flavors, but it happens to be one of the most thoroughly tested principles in physics. (Many scholar have argued that the equivalence principle is actually false, but only in a sense that makes it irrelevant to the validity of general relativity.) It seems most likely that if general relativity fails, it would be because one or more of its "simplicities" is inappropriate. For example, the restriction to second order equations, or the assumption of Riemannian metrics rather than, say, Finsler metrics, or the naive assumption of R⁴ topology, or perhaps even the basic assumption of a continuum. Still, each of these would also have conceptual implications for the special theory, so these aren't valid reasons for continuing to regard special relativity as a separate theory.

Suppose we naively superimpose special relativity on Newtonian physics, and adopt a naive definition of "inertial worldline", such as a worldline with no locally sensible acceleration. On that basis we find that there can be multiple distinct "inertial" worldlines connecting two given events (e.g., intersecting elliptical orbits of different eccentricities), which conflicts with the special relativistic principle of a unique inertial interval between any pair of timelike separated events. To press the antinomy analogy further, we could arrange to have special relativity conclude that each of these worldlines has a lesser lapse of proper time than each of the others. (If the barber shaves everyone who doesn't shave himself, who shaves the barber?) Of course, with special relativity (as with set theory) we can easily block such specific conundrums - once they are pointed out - by imposing one or more restrictions on the definition of "inertial" (or the definition of a "set"), and in so doing we make the theory somewhat less naive, but the experience raises legitimate questions about whether we can be sure that we have blocked all possible antinomies.

We shouldn't push the analogy too far, since there are obvious differences between a purely mathematical theory and a physical theory, the latter being exposed to potential conflict with a much wider class of "external" constraints (such as the requirement to possess a consistent mapping to a representation of experience). Nevertheless, when considering naive set theory's assumption of the existence of sets, and its assertions about how to manipulate and reason with sets, all in the absence of a comprehensive and reliable criteria of how to identify what can legitimately be called a set, there is an interesting parallel with special relativity's assumption of the existence of inertial frames and how to reason with them and in them, all in the absence of a comprehensive and reliable framework for deciding what does and what does not constitute an inertial frame.

It might be argued that relativity is a purely formalistic theory, which simply assumes an inertial frame is specified, without telling how to identify one. Certainly we can completely insulate special relativity from any and all conflict by simply adopting this strategy, i.e., asserting that special relativity avers no mapping at all between it's elements and the objects of our experience. This strategy effectively blocks falsification, but it also renders the theory meaningless from a physical standpoint. Moreover, even recognizing the distinction between logical inconsistency and empirical falsification, we must also remember that the rules of logic and reason are ultimately grounded in "observations", albeit of a very abstract nature, and mathematical theories no less than physical theories are attempts to formalize "observations". As such, they are comparably subject to upset when they're found to conflict with other observations (such as barbers or gravity).

It might also be argued that we cannot really attribute any antinomies to special relativity, because the cases noted above (multiply intersecting elliptical orbits, etc) arise only from attempting to apply special relativistic reasoning to a class of entities for which it is not suited. However, the same is true of naive set theory, i.e., it works perfectly well when applied to a wide class of sets, but leads to logically impossible conclusions if we attempt to apply it to a class of sets that "act on themselves"... just as gravity is found to act on itself in the general theory. In a real sense, gravity in general relativity is a self-referential phenomenon, as revealed by the non-linearity of the field equations. Notice that our antinomies in the special theory arise only when trying to reason with "self-referential inertial frames", i.e., in the presence of irreducible gravitational fields.

The basic point is that although special relativity serves as the local limiting case of the general theory, it is not able to stand alone, because it cannot identify the phenomena to which it is applicable, and this renders it incapable of yielding definite macroscopic conclusions about the physical world. Given all the indeterminate qualifiers on the scope of its applicability, we effectively remove special relativity from the set of physical theories. This just re-affirms the point that any application of special relativity is, strictly speaking, legitimized only within the context of the general theory, which provides the framework for assessing the validity of the application. We can, of course, still practice the special theory from a naive standpoint, and be quite successful at it, just as we can practice naive set theory without running into trouble very often. Naturally none of this implies that special relativity, by itself, is unfalsifiable. Indeed it is falsifiable, but only when superimposed on some other framework (such as Newtonian physics) and combined with some auxiliary assumptions about how to identify inertial frames. In fact, the special theory of relativity is not only falsifiable, it is falsified, and was superceded in 1915 by a superior and more comprehensive theory. Of course, strict epistemological scruples don't have a great deal of relevance to the actual day-to-day practice of science.

From a more formal standpoint, it's interesting to consider the correspondence between the foundations of set theory and the theories of relativity. The archetypal example of a problematic concept in naive set theory was the notion of the "set of all sets". It soon became apparent to Cantor, Russell, Frege, and other mathematicians that this plausible- sounding notion could not consistently be treated as a set in the usual sense. The problem was recognized to be the self-referential nature of the concept. We can compare this to the general theory of relativity, which is compelled by the equivalence principle to represent the metric of spacetime as (so to speak) "the field of all fields". To make this more precise, recall that Newtonian gravity can be represented by a scalar field φ defined over a pre-existing metrical space, whose metric we may denote as g. The vacuum field equation is L_g(φ) = 0 where L_g signifies the Laplacian operator over the space with the fixed metric g. In general relativity the Laplacian is replaced by a more complicated operator R_g which, like the Laplacian, is effectively a differential operator whose components are evaluated on the spacetime with the metric g. However, in general relativity the field on which R_g operates is nothing but the spacetime metric g itself. In other words, the vacuum field equations are R_g(g) = 0. The entity R_g(g) is called the Ricci tensor in differential geometry, usually denoted in covariant form as R_μν.

This highlights the essentially self-referential nature of the Einstein field equations, as opposed to the Newtonian field equations where the operator and the field being operated on are completely independent entities. It's interesting to compare this situation to schematic representations of Goedel's formalization of arithmetic, leading to his proof of the Incompleteness Theorem. Given a well-defined mapping between single-variable propositional statements and the natural numbers (which Goedel showed is possible, though far from trivial), let P_n(w) denote the nth statement applied to the variable w. Since every possible proposition maps to some natural number, there is a natural number k such that P_k(w) represents the proposition that P_w(w) has no proof. But then what happens if we set the variable w equal to k? We see that P_k(k) represents that proposition that there is no proof of P_k(k), from which it follows that if there is no proof of P_k(k) then P_k(k) is true, whereas if there is a proof of P_k(k) then P_k(k) is false. Hence, assuming our system of arithmetic is self-consistent, so that it doesn't contain proofs of false propositions, we must conclude that P_k(k) is true but unprovable. Obviously the negation of P_k(k) must also be unprovable, assuming our arithmetic is consistent, so the proposition is strictly undecidable within the formal system encoded by our numbering scheme.

The analogy between Goedel’s propositions P_k(k) and the field equations of general relativity R_g(g) = 0 should not be pressed too far, but it does hint at the real and profound subtleties that can arise when we allow self-referential statements. It’s worth noting that, like set theory and the theory of relativity, the other great branch of physics developed during the 20th century – quantum physics – also emerged as a theory with two different levels. The first level is ordinary quantum mechanics, which assigns to each classical particle a quantum field. Then, in order to account for the creation and annihilation of particles during their interactions (and also to achieve consistency with special relativity), it was found necessary to introduce “second quantization”, leading to quantum field theory, which is essentially a consideration of (again!) “the field of all fields”. Thus the two great competetors for the soul of physics, namely, general relativity and quantum field theory, both emerged out of the necessity to place their more naïve predecessors (special relativity and quantum mechanics) into a more comprehensive context, and to encompass a broader range of interactions. The results are two theories, each of which attempts, in very different ways, to represent the field of all fields.

It's interesting that Einstein seems to have been mindful very early of the eventual necessity of such considerations, although he deferred it for quite some time. Prior to 1905 many physicists were attempting to construct a purely electromagnetic theory of matter based on Maxwell's equations, according to which "the particle would be merely a domain containing an especially high density of field energy". However, in presenting the special theory of relativity Einstein carefully avoided proposing any particular theory as to the ultimate structure of matter, and showed that a purely kinematical interpretation could account for the relation between energy and inertia. He took this approach not because he was disinterested in the nature of matter, but because he recognized immediately that

Maxwell's equations did not permit the derivation of the equilibrium of the electricity that constitutes a particle. Only different, nonlinear field equations could possibly accomplish such a thing. But no method existed for discovering such field equations without deteriorating into adventurous arbitrariness.

So in 1905 Einstein took the more conservative route and merely(!) redefined the traditional concepts of time and space. A few years later he himself embarked on an adventure leading ultimately in 1915 to the non-linear field equations of general relativity, but even in this he managed to make important progress by again side-stepping the question of the ultimate constituency of matter and light. As he recalled in his Autobiographical Notes

It seemed hopeless to me at that time to venture the attempt of representing the total field [as opposed to the pure gravitational field] and to ascertain field laws for it. I preferred, therefore, to set up a preliminary formal frame for the representation of the entire physical reality; this was necessary in order to be able to investigate, at least preliminarily, the effectiveness of the basic idea of general relativity.

In his later years it seems Einstein had decided he had made all the progress that could be made on this preliminary basis, and set about the attempt to represent the total field. He wrote the above comments in 1949, after a quarter-century of fruitless efforts to discover the non-linear equations for the "total field", including electromagnetism and matter, so he knew only too well the risks of deteriorating into adventurous arbitrariness.

Return to Table of Contents