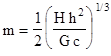4.4  Force, Curvature, and Uncertainty

 

The atoms, as their own weight bears them down plumb through the void, at scarce determined times, in scarce determined places, from their course decline a little - call it, so to speak, mere changed trend. For were it not their wont thuswise to swerve, down would they fall, each one, like drops of rain, through the unbottomed void; and then collisions ne'er could be, nor blows among the primal elements; and thus Nature would never have created aught.

                                                  Lucretius, 50 BC

 

The trajectory of radial non-rotating gravitational freefall can be expressed by the simple differential equation

 

 

where k is a constant and dots signify derivatives with respect to time. This equation is valid for both Newtonian gravity and general relativity, provided we identify Newton's time parameter with the free-falling particle's proper time, and Newton's radial distance with the radial Schwarzschild coordinate. Notice that no gravitational constant appears in this equation (k is just a constant of integration determined by the initial conditions), so equation (1) is a purely kinematic description of gravity. Why did Newton not adopt this simple kinematic view? Historically the reasons involved considerations of rotating systems, but the basic problem with the kinematic view is present even with simple non-rotating free-fall.

 

The problem is that equation (1) has an unrealistic "static solution" at . This condition implies that k=0, and the separation between the two objects has no proper "trajectory" (i.e., time drops out of the equation), so the equation cannot extrapolate the position forward or backward in time. Of course, this condition can never arise naturally from any non-static condition with k ≠ 0, but we can imagine that by the imposition of some external force we can arrange to have the two objects initially at rest and not accelerating relative to each other. Then when the objects are released from the "outside" force we expect them to immediately begin falling toward each other under the influence of their mutual gravitational attraction. This implies that k, and therefore , must immediately assume some non-zero values, but equation (1) gives us no information about these values, because the entire equation identically vanishes at the static solution.

 

To escape from the static solution, Newtonian mechanics splits the kinematic equation of motion into two parts, coupled together by the dynamical concepts of force and mass. Two objects are said to exert (equal and opposite) force on each other proportional to the inverse of the square of the separation between them, and the second derivative of that separation is proportional (per mass) to this force. Thus, the relation between separation and time for two identical particles, each of mass m, is given not by a single kinematic equation but by two simultaneous equations

 

 

If we combine these two equations by eliminating F, we have

 

 

which shows that when the two objects are released, the separation instantly acquires the second derivative −2Gm/s2. Once this "initialization" has been accomplished, the subsequent free fall is entirely determined by equation (1), as can be seen by differentiating (2) to give

 

 

which, assuming the separation is not zero, can be divided by s to give , the derivative of (1). This shows that, for non-rotating radial free-fall, the coupling parameters F and m are entirely superfluous except that they serves to establish the proper initial condition when the two objects are released from rest. Thus, Newton's dual concepts of force-at-a-distance and the proportionality of acceleration to force serve only (in this context) to enable us to solve for a non-vanishing  as a function of s when  = 0, which equation (1) obviously cannot do.

 

Furthermore, the constant G does not appear in (1) or (3), even though they give a complete description of gravitational free-fall except for the singularity at  = 0. Thus the gravitational constant is also needed only at this singular point, the "static solution" of equation (1), which is the only point at which the dynamical concepts of force and mass are used. Aside from this singular condition, non-rotating radial Newtonian gravity is a purely kinematical phenomenon.

 

There are several essentially equivalent formulations of the kinematic equation of non-rotating radial gravitational motion, but all lead to an indeterminate condition at the static solution. For example, if we set k = β/2α in equation (1) and multiply through by 2 we have . Integrating this over time gives  where γ is a constant of integration. Dividing by s gives

 

 

which we recognize as expressing the classical conservation of energy, with the first term representing potential energy and the second term denoting kinetic energy. Taking the derivative of this gives

 

 

Notice that in each of the preceding equations the condition  still represents a solution for any s, even though it is unrealistic. At this point we may be tempted to solve our problem by dividing through equation (4) by to give

 

 

 which is the Newtonian inverse-square "force" law of gravity. This does indeed determines the second derivative  as a function of s, and thereby provides the information needed to depart from the externally imposed static initial condition. However, notice that the condition which concerns us is precisely when = 0, so when we divided equation (4) by we were essentially just eliminating the singular pole arbitrarily by dividing by zero. Thus we can't properly say that the "force-at-a-distance" law (5) follows from equation (1). The removal of the indeterminate singularity actually represents an independent assumption relative to the basic kinematic equation of motion.

 

Of course, this assumption is perfectly compatible with the equation of motion, as can be seen by solving equation (5) for g/s and substituting into the energy equation to give

 

and thus

 

which is the same as equation (1). This compatibility is a necessary consequence of the fact that the equation of motion is totally indeterminate when =0, which is the only condition at which the force law introduces new information not contained in the basic equation of motion.

 

In view of the above relations, it is not surprising that in the general theory of relativity we find gravity expressed without the concept of force. Einstein avoided the problem of the static solution - without invoking an auxiliary concept such as force - simply by recasting the phenomena in four-dimensional space-time, within which no material object is ever static. Every object, even one "at rest" in space, necessarily has a proper trajectory through spacetime, because it's moving forward in time. Furthermore, if we allow the spacetime manifold to posses intrinsic curvature, it follows that a purely time-like trajectory can "veer off" and acquire space-like components.

 

Of course, this tendency to "veer off" depends on the degree of curvature of the space-time, which general relativity relates to the mass-energy in the region. One of Einstein's motivations for the general theory was the desire to eliminate arbitrary constants, particularly the gravitational constant G, from the expressions of physical laws, but in the general theory it is still necessary to determine the proportionality between mass and curvature empirically, so the arbitrary gravitational constant remains. In any case, we see that Newtonian mechanics and general relativity give formally identical relations between separation and time for non-rotating free-fall, and the conceptual differences between the two theories can be expressed in terms of the ways in which they escape from or avoid the static condition.

 

It's interesting to note that the static solution of (1) is unstable in the direction collapse. Given a positive separation s, the signs of  must be {+,−}, {+,+}, {−,+} or {−,−} in order to satisfy (1), but considering small perturbations of these derivatives from the state in which they are both zero, it's clear that {+,−} is unrealistic, because  would not go positive from zero while  was going negative from zero. For similar reasons, perturbations leading to {+,+} and {−,+} are also excluded. Only the case {−,−} represents a realistic outcome of a small perturbation from the static solution.

 

This instability in the direction of collapse suggests another approach to escaping from (or avoiding) the static solution. The exact velocity and position of the two objects cannot be known at the quantum level, so, in a sense, the closest that two bodies can come to a static condition must still allow the equivalent of one quanta of momentum in their relative velocities. It's tempting to imagine that there might be some way of deriving the gravitational constant based on the idea that the initial condition for (1) is determined by the characteristic quantum uncertainty for the separations between massive particles, since, as we've seen, this initial condition fully determines the trajectory of radial gravitational free-fall. Simplistically we could note that, for a particle of mass m, any finite limit L on allowable distances implies two irreducible quantities of energy per unit mass, one being (h/2L)2/2m2 corresponding to the minimum "observable" momentum mv = h/2L (where h is Planck's constant) due to the uncertainty principle, and the other being the minimum gravitational potential energy Gm/L. Identifying these two energies with each other, and setting L equal to the event horizon radius c/H where c is the velocity of light and H is Hubble's expansion constant, we have the relation

 

 

Inserting the values h = (6.625)10−34 J sec, G = (6.673)10−11 Nm2/kg2, c = (2.998)108 m/sec, and H = (2.3)10−18 sec−1 gives a value of (1.8477)10−28 kg for the characteristic mass m, which happens to be about one ninth the mass of a proton. Rough relationships of this kind between the fundamental physical constants have been discussed by Dirac and others, including Leopold Infeld, who wrote in 1949

 

Let us take as an example Maxwell’s equations and try to find their solution on a cosmological background… In a closed universe the frequency of radiation has a lowest value [corresponding to the maximum possible wavelength]. The spectrum, on its red side, cannot reach frequency zero. We obtain characteristic values for frequencies… a similar situation prevails if we consider Dirac’s equations upon a cosmological background. The solutions in a closed universe are different, not because of the metric, but because of the topology of our universe.

 

Such ideas are intiguing, but they have yet to be incorporated meaningfully into any successful physical theory.

 

The above represents a very simplistic sense in which the uncertainty of quantum mechanics and the spacetime curvature of general relativity can be regarded as two alternative conceptual strategies for establishing a consistent gravitational coupling. In a more sophisticated sense, we can find other interesting formal parallels between these two concepts, both of which fundamentally express non-commutativity. Given a system of orthogonal xyz coordinates, let A,B,C denote operations which, when applied to any unit vector emanating from the origin, rotate that vector in the positive sense about x, y, or z axis respectively. Each of these operations can be represented by a rotation matrix, such that multiplying any vector by that matrix will effectively rotate the vector accordingly. As Hamilton realized in his efforts to find a three-dimensional analog of complex numbers (which represent rotation operators in two-dimensions), the multiplication (i.e., composition) of two rotations in space is not commutative. This is easily seen in our example, because if we begin with a vector V emanating from the origin in the positive z direction, and we first apply rotation A and then rotation B, we arrive at a vector pointing in the positive y direction, whereas if we begin with V and apply the rotation B first and then A we arrive at a vector pointing in the negative x direction. Thus the effect of the combined operation AB is different from the effect of the combined operation BA, and so the matrix AB − BA does not vanish. This is in contrast with ordinary scalars and complex numbers, which always satisfy the commutivity relation ab − ba = 0 for every two numbers a,b.

 

This non-commutivity also appears when dealing with calculus on curved manifolds, which we will discuss in more detail in Section 5. Just to give a preliminary indication of how non-commutative relations arise in this context, suppose we have a vector field Tα defined over a given metrical manifold, and we let Tαμν denote covariant differentiation of Tα first with respect to the coordinate xμ and then with respect to the coordinate xν. In a flat manifold the covariant derivative is identical to the partial derivative, which is commutative. In other words, the result of differentiation with respect to two coordinates in succession is independent of the order in which we apply the differentiations. However, in a curved manifold this is not the case. We find that reversing the order of the differentiations yields different results, just as when applying two rotations in succession to a vector. Specifically, we will find that

 

 

where Rσαμν is the Riemann curvature tensor, to be discussed in detail in Section 5.7. The vanishing of this tensor is the necessary and sufficient condition for the manifold to be metrically flat, i.e., free of intrinsic curvature, so this tensor can be regarded as a measure of the degree of non-commutivity of covariant derivative operators in the manifold.

 

Non-commutivity also plays a central role in quantum mechanics, where observables such as position and momentum are represented by operators, much like the rotation operators in our previous example, and the possible observed states are eigenvalues of those operators. If we let X and P denote the position and momentum operators, the application of one of these operators to the state vector of a given system results in a new state vector with specific probabilities. This represents a measurement of the respective observable. The effect of a position measurement followed by a momentum measurement can be represented by the combined operator XP, and likewise the effect of a momentum measurement followed by a position measurement can be represented by PX. Again we find that the commutative property does not generally hold. If two observable are compatible, such as the X position and the Y position of a particle, then the operators commute, which means we have XY − YX = 0. However, if two operators are not compatible, such as position and momentum, their operators do not commute. This leads to the important relation

 

 

This non-commutivity in the measurement of observables implies an inherent limit on the precision to which the values of the incompatible observables can be jointly measured. In general it can be shown that if A and B are the operators associated with the physical quantities a and b, and if Δa and Δb denote the expected root mean squares of the deviations of measured values of a and b from their respective expected values, then

 

 

This is Heisenberg's uncertainty relation. The commutator of two observable operators is invariably a multiple of Planck's constant, so if Planck's constant were zero, all observables would be compatible, i.e., their operators would commute, just as do all classical operators. We might say (with some poetic license) that Planck's constant is a measure of the "curvature" of the manifold of observation. This "curvature" applies only to incompatible observables, although the term "incompatible" is somewhat misleading, because it actually signifies that two observables A,B are conjugates, i.e., transformable into each other by the conjugacy relation A=UBU−1 where U is a unitary operator (analagous to a simple rotation operator).

 

Return to Table of Contents