3.7  Zeno and the Paradox of Motion

We may say a thing is at rest when it has not changed its position between now and then, but there is no ‘then’ in ‘now’, so there is no being at rest. Both motion and rest, then, must necessarily occupy time.

                                                                Aristotle, 350 BC

The Eleatic school of philosophers was founded by Xenophanes (born c. 570 BC), who emphasized the unity and immutability of God and the universe - "The all is one and the one is God." The colony of Elea was founded by a group of Ionian Greeks who, in 545 BC, had been besieged in their seaport city of Phocaea by an invading Persian army, and were ultimately forced to evacuate by sea. They sailed to the island of Corsica, and occupied it after a terrible sea battle with the navies of Carthage and the Etruscans. Just ten years later, in 535 BC, the Carthaginians and Etruscans regained the island, driving the Phocaean refugees once again into the sea. This time they landed on the southwestern coast of Italy and founded the colony of Elea, seizing the site from the native Oenotrians. All this happened within the lifetime of Xenophanes, himself a wandering exile from his native city of Colophone in Ionia, from which he too had been force to flee in 545 BC. He lived in Sicily and then in Catana before finally joining the colony at Elea. It's tempting to speculate on how these events may have psychologically influenced the Eleatic school's belief in permanent unalterable oneness.

The greatest of the Eleatic philosophers was Parmenides (born c. 539 BC), who developed the theme of unchanging oneness, and extended it to all Being. He argued that multiplicity, motion, and change were mere appearances. He is also sometimes credited with originating the use of logical argument in philosophy. His habit was to accompany each statement of belief with some kind of logical argument for why it must be so. This may have been a conscious innovation, or perhaps habitual rationalization was simply a peculiar aspect of his intellect. In any case, on this basis he is sometimes regarded as the father of metaphysics, and, as such, a key contributor to the evolution of scientific thought.

Parmenides's belief in the absolute unity and constancy of reality is quite radical and abstract, even by modern standards. He maintained that the universe is literally singular and unchangeable. However, his rationalism forced him to acknowledge that appearances are to the contrary, i.e., while he flatly denied the existence of plurality and change, he admitted the appearance of these things. Nevertheless, he insisted these were mere perceptions and opinions, not to be confused with "what is". Not surprisingly, Parmenides was ridiculed for his beliefs. One of Parmenides' students was Zeno, who is best remembered for a series of arguments in which he defends the intelligibility of the Eleatic philosophy by purporting to prove, by logical means, that change (motion) and plurality are impossible.

We can't be sure how the historical Zeno intended his arguments to be taken, since none of his writings have survived. We know his ideas only indirectly through the writings of Plato, Aristotle, Simplicus, and Proclus, none of whom was exactly sympathetic to Zeno's philosophical outlook. Furthermore, we're told that Zeno's arguments were a "youthful effort", and that they were made public without his prior knowledge or consent. Also, even if we accept that his purpose was to defend the Eleatic philosophy against charges of logical inconsistency, it doesn't follow that Zeno necessarily regarded his counter-charges as convincing. It's conceivable that he intended them as satires of (what he viewed as) the fallacious arguments that had been made against Parmenides' ideas. In any case, although we cannot know for sure how Zeno himself viewed his "paradoxes", we can nevertheless examine the arguments themselves, as they've come down to us, to see if they contain − or suggest − anything of interest.

Of the 40 arguments attributed to Zeno by later writers, the four most famous are on the subject of motion:

The Dichotomy: There is no motion, because that which is moved must arrive at the middle before it arrives at the end, and so on ad infinitum.

The Achilles: The slower will never be overtaken by the quicker, for that which is pursuing must first reach the point from which that which is fleeing started, so that the slower must always be some distance ahead.

The Arrow: If everything is either at rest or moving when it occupies a space equal to itself, while the object moved is always in the instant, a moving arrow is unmoved.

The Stadium: Consider two rows of bodies, each composed of an equal number of bodies of equal size. They pass each other as they travel with equal velocity in opposite directions. Thus, half a time is equal to the whole time.

The first two arguments are usually interpreted as critiques of the idea of continuous motion in infinitely divisible space and time. They differ only in that the first is expressed in terms of absolute motion, whereas the second shows that the same argument applies to relative motion. Regarding these first two arguments, there's a tradition among some high school calculus teachers to present them as "Zeno's Paradox", and then "resolve the paradox" by pointing out that an infinite series can have a finite sum. This may be a useful pedagogical device for beginning calculus students, but it misses an interesting and important philosophical point implied by Zeno's arguments. To see this, we can re-formulate the essence of these two arguments in more modern terms, and show that, far from being vitiated by the convergence of infinite series, they actually depend on the convergence of the geometric series.

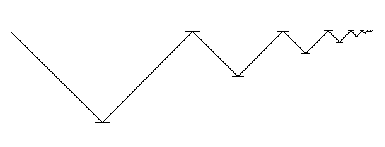
Consider a ray of light bouncing between an infinite sequence of mirrors as illustrated below

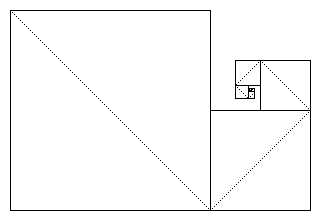
On the assumption that matter, space, and time are continuous and infinitely divisible (scale invariant), we could conceive of a point-like massless “particle of light” traveling at constant speed through a sequence of mirrors whose sizes and separations decrease geometrically (e.g., by a factor of two) on each step. The envelope around these mirrors is clearly a wedge shape that converges to a point, and the total length of the zigzag path is obviously finite (because the geometric series 1 + 1/2 + 1/4 + ... converges, as can be seen from Euclid’s formula), so the particle must reach "the end" in finite time. The essence of Zeno's position against continuity, infinite divisibility, and scale invariance is that there is no logical way for the photon to emerge from the sequence of mirrors. The direction in which the photon would be traveling when it emerged would depend on the last mirror it hit, but there is no "last" mirror. Similarly we could construct "Zeno's maze" by having a beam of light directed around a spiral as shown below:

Again the total path is finite, but has no end, i.e., no final direction, and a ray propagating along this path can neither continue nor escape. Modern readers may feel entitled to disregard this line of reasoning, knowing that matter consists of atoms which are not infinitely divisible, and not scale invariant, so we could never construct an infinite sequence of geometrically decreasing mirrors. Also, every photon has some finite scattering wavelength and thus cannot be treated as a "point particle". Furthermore, even a massless particle such as a photon necessarily has momentum according to the quantum and relativistic relation p = h/λ, and the number of rebounds per unit time – and hence the outward pressure on the structure holding the mirrors in place − increases to infinity as the photon approaches the convergent point. However, these arguments merely confirm Zeno's position that the physical world is not scale-invariant or infinitely divisible (noting that Planck’s constant h represents an absolute scale). Thus, we haven't debunked Zeno, we've merely conceded his point – a point which is not, in itself, paradoxical. It simply indicates that at some level the physical world must have an absolute scale and be regarded as consisting of finite indivisible entities. We arrive at Zeno's paradox only when these arguments against infinite divisibility are combined with the complementary set of arguments (The Arrow and The Stadium) which show that a world consisting of finite indivisible entities is also logically impossible, thereby presenting us with the conclusion that physical reality can be neither continuous nor discontinuous (i.e., discrete).

The more famous of Zeno's two arguments against discontinuity is "The Arrow", which focuses on the instantaneous physical properties of a moving arrow. He notes that if physical objects exist discretely at a sequence of discrete instants of time, and if no motion occurs in an instant, then we must conclude that there is no motion in any given instant. (Bertrand Russell commented that this is simply "a plain statement of an elementary fact".) But if there is literally no physical difference between a moving and a non-moving arrow in any given discrete instant, then how does the arrow know from one instant to the next if it is moving? In other words, how is causality transmitted forward in time through a sequence of instants, in each of which motion does not exist?

It's been noted that Zeno's "Arrow" argument could also be made in the context of continuous motion, where in any single slice of time there is (presumed to be) no physical difference between a moving and a non-moving arrow. Thus, Zeno suggests that if all time is composed of instants (continuous or discrete), and motion cannot exist in any instant, then motion cannot exist at all. A naive response to this argument (at least in the continuous form) is to point out that although the value of a function f(t) is constant for a given t, the function f(t) may be non-constant at t. But, again, this explanation doesn't really address the philosophical issue raised by Zeno's argument. A continuous function (as emphasized by Weierstrass) is a static completed entity, so by invoking this model we are essentially agreeing with Parmenides that physical motion does not truly exist, and is just an illusion, i.e., "opinions", arising from our psychological experience of a static unchanging reality.

Of course, to accomplish this we have expanded our concept of "the existing world" to include the time dimension (“block universe”). If, instead, we insist on adhering to the view of the entire physical world as a purely spatial expanse, existing in and progressing through a sequence of instants, then we again run into the problem of how a quality that exists only over a range of instants can be causally conveyed through any given instant in which it has no form of existence. Before blithely dismissing this concern as non-sensical, it's worth noting that modern physics has concluded (along with Zeno) that the classical image of space and time was fundamentally wrong, and in fact motion would not be possible in a universe constructed according to the classical model. We now recognize that position and momentum are incompatible variables, in the sense that an exact determination of either one of them leaves the other completely indeterminate. According to quantum mechanics, the eigenvalues of spatial position are incompatible with the eigenvalues of momentum so, just as Zeno’s arguments suggest, it really is inconceivable for an object to exhibit a definite position and momentum (motion) simultaneously.

Also, the theory of special relativity answers Zeno's concern over the lack of an instantaneous difference between a moving and a non-moving arrow by positing a fundamental re-structuring of the basic way in which space and time fit together, such that there really is an instantaneous difference between a moving and a non-moving object, insofar as it makes sense to speak of "an instant" of a physical system with mutually moving elements. Objects in relative motion have different planes of simultaneity, with all the familiar relativistic consequences, so not only does a moving object look different to the world, but the world looks different to a moving object. For example, an arrow in motion is spatially contracted (or rather, hyperbolically rotated in spacetime) compared to the same arrow at rest.

This resolution of the paradox of motion presumably never occurred to Zeno, but it's no exaggeration to say that special relativity vindicates Zeno's skepticism and physical intuition about the nature of motion. He was correct that instantaneous velocity in the context of absolute space and absolute time does not correspond to physical reality, and probably doesn't even make sense. From Zeno's point of view, the classical concept of absolute time was not logically sound, and special relativity (or something like it) is a logical necessity, not just an empirical fact. It's even been suggested that if people had taken Zeno's paradoxes more seriously they might have arrived at something like special relativity centuries ago, just on logical grounds. This suggestion goes back at least to Minkowski's famous lecture of "staircase wit" (see Section 1.7). Doubtless it's stretching the point to say that Zeno anticipated the theory of special relativity, but it's undeniably true that his misgivings about the logical consistency of motion in it's classical form were substantially justified. The universe does not (and, arguably, could not) work the way people thought it did.

In all four of Zeno's arguments on motion, the implicit point is that if space and time are independent, then logical inconsistencies arise regardless of whether the physical world is continuous or discrete. All of those inconsistencies can be traced to the implication that, if any motion is possible, then the range of conceivable relative velocities must be unbounded, corresponding to Minkowski's "unintelligible" G_∞.

What is the alternative? Zeno considers the premise that the range of possible relative velocities is bounded, i.e., there is some maximum achievable (conceivable) relative velocity, and he associates this possibility with the idea that space and time are not infinitely divisible. (It presumably didn't occur to him that another way of achieving this is to assume space and time are not independent.)

This brings us to the last of Zeno's four main arguments on motion, "The Stadium", which has always been the most controversial, partly because the literal translation of its statement is somewhat uncertain. In this argument Zeno appears to be attacking the only remaining alternative to the unintelligible G_∞, namely, the possibility of a finite upper bound on conceivable velocity. It's fascinating that he argues in much the same way that modern students do when they're first introduced to the concept of an invariant speed in the theory of special relativity. He says, in effect, that if someone is running towards me from the west at the maximum possible speed, and someone else is approaching me from the east at the maximum possible speed, then they are approaching each other at twice the maximum possible speed, which is a contradiction.

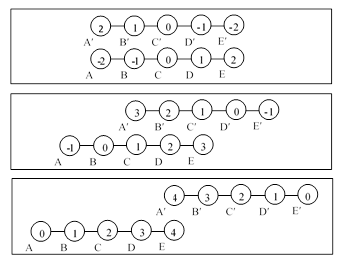
To illustrate the relevance of Zeno's arguments to a discussion of the consequences of special relativity, compare the discussion of time dilation in Section 2.13 of Rindler's "Essential Relativity" with Heath's review of Zeno's Stade paradox in Chapter VIII of "A History of Greek Mathematics". The resemblance is so striking that it's tempting to imagine that either Rindler consciously patterned his discussion on some recollection of Zeno's argument, or it's an example of Jung's collective unconscious. Here is a reproduction of Rindler's Figure 2.4, showing three "snapshots of two sequences of clocks A, B, C,... and A′, B′, C′, ... fixed at certain equal intervals along the x axes of two frames S and S':

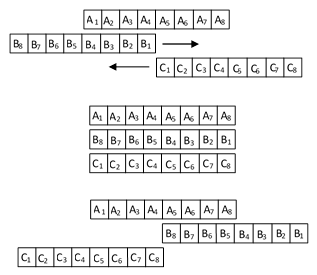
These three snapshots are taken at equal intervals by an observer in a third frame S″, relative to which S and S′ have equal and opposite velocities. Rindler describes the values that must appear on each clock in order to explain the seemingly paradoxical result that each observer considers the clocks of the others to be running slow, in accord with Einsteinian relativity. Compare this with the figure on page 277 of Heath:

where again we have three snapshots of a sequence of clocks (i.e., observers/athletes), this time showing the reference frame S″ as well as the two frames S and S′ that are moving with equal and opposite velocities relative to S". As Aristotle commented, this scenario evidently led Zeno to the paradoxical conclusion that "half the time is equal to its double", precisely as the freshman physics student suspects when he first considers the implications of relativity.

Surely we can forgive Zeno for not seeing that his arguments can only be satisfactorily answered − from the standpoint of physics − by assuming Lorentzian invariance and the relativity of space and time. According to this view, with it's rejection of absolute simultaneity, we're inevitably led from a dynamical model in which a single slice of space progresses "evenly and equably" through time, to a purely static representation in which the entire history of each worldline already exists as a completed entity in the plenum of spacetime. This static representation, according to which our perceptions of change and motion are simply the product of our advancing awareness, is strikingly harmonious with the teachings of Parmenides, whose intelligibility Zeno's arguments were designed to defend.

Have we now finally resolved Zeno's "youthful effort"? Given the history of "final resolutions", from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of "Rorschach image", which people can interpret in terms of their most fundamental philosophical concerns (if they have any).

Return to Table of Contents