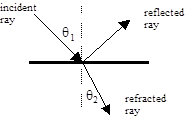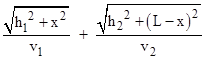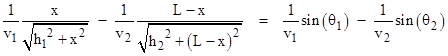3.4  Stationary Paths

Then with no throbbing fiery pain,

No cold gradations of decay,

Death broke at once the vital chain,

And free’d his soul the nearest way.

                             Samuel Johnson, 1783

The apparent bending of visual images of objects partially submersed in water was noted in antiquity, but the first published attempt to quantify the effect was in Kepler's Dioptrice (1611). Kepler reported that, at least for rays nearly perpendicular to the surface, the ratio of the angles of incidence and refraction is (nearly) proportional to the ratio of what we now call the indices of refraction of the media. Originally these indices were just empirically determined constants for each substance, but Newton later showed that for most transparent media the refractive index could be taken as unity plus a term proportional to the medium's density. Incidentally, Kepler also noticed that with suitable materials and angles of incidence, the refracted angle can be made to exceed 90 degrees, resulting in total internal reflection, a phenomenon that is exploited in modern fiber optics.

In 1621, Willebrord Snell performed a series of careful measurements and found that when a ray of light passes through a surface at which the index of refraction changes abruptly, the angles made by the incident and transmitted rays with the respective outward normals to the surface are related according to the simple formula (now called Snell's Law)

where n₁ and n₂ are the indices of refraction (still regarded simply as empirical constants for any given medium) on the incident and transmitted sides of the boundary, and θ₁ and θ₂ are the angles that the incident ray and the transmitted ray make with the normal to the boundary as shown below.

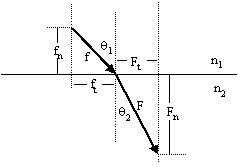
Soon thereafter, Descartes published his La Dioptrique (1637), in which he presented a rationalization of Snell's law based on the idea that light is a kind of pressure transmitted instantaneously (or nearly so) through an elastic medium. Descartes' theory led to a fascinating scientific dispute over the correct interpretation of light. According to Descartes' mechanistic description, a dense medium must transmit light more effectively, i.e., with more "force", than a less dense medium. (He sometimes described light rays in terms of a velocity vector rather than a force vector, but in either case he reasoned that the magnitude of the vector, which he called the light's determination, increased in proportion to the density of the medium.) Also, Descartes argued that the tangential component of the ray vector remains constant as the ray passes through a boundary. On the basis of these two (erroneous) premises, the parallelogram of forces (or velocities) for a ray of light passing from a less dense to a more dense medium is as shown below.

The magnitude of the incident force is f, and the magnitude of the refracted force is F, each of which is decomposed into components normal and tangential to the surface. Since Descartes assumes f_t = F_t, it follows immediately that f sin(θ₁) = F sin(θ₂). If, as Descartes often did, we regard the force (determination) of the light as analogous to the speed of light, then this corresponds to the relation v₁ sin(θ₁) = v₂ sin(θ₂) where v₁ and v₂ are the speeds of light in the two media.

Fermat criticized Descartes' derivation, partly on mathematical grounds, but also because he disagreed with the basic physical assumptions. In particular, Fermat believed that light must not only travel at a finite speed, it must travel slower (not faster) in a denser medium. Thus he argued that the derivation of Snell's law presented by Descartes was invalid, and he suspected the law itself might even be wrong. In his attempts to derive the "true" law of refraction, Fermat recalled the derivation of the law of reflection given by Hero of Alexandria in ancient times. (Actually, Fermat got this idea by way of his friend Marin Careau, who had repeated Hero's derivation in a treatise on optics in 1657.) Hero asserted that light moves in a straight line in empty space, and reflects at equal angles when striking a mirror, for the simple reason that light prefers always to move along the shortest possible path. As Archimedes had pointed out, the shortest path between two given points in space is a straight line, and this (according to Hero) explains why light rays are straight. More impressively, Hero showed that when travelling from some point A to the surface of a plane mirror and then back out to some point B, the shortest path is the one for which the angles of incidence and reflection are equal. These are ingenious observations, but unfortunately the same approach doesn't explain refraction, because in that case the shortest path between a point above water and a point below water (for example) would always be simply a straight line, and there would be no refraction at all.

At this point Fermat's intuition that light propagates with a characteristic finite speed, and that it moves slower in denser media, came to his aid, and he saw that both the laws of reflection and refraction (as well as rectilinear motion in free space) could be derived from the same principle if, instead of light traveling along a path that minimizes the spatial distance, we suppose it travels along the path that minimizes the temporal distance, i.e., light follows the path to its destination that will take the least possible time. This conceptual step is fascinating for several reasons. For one thing, we don't know on what basis Fermat "intuited" that the speed of light is not only finite (which had never yet been demonstrated), but that it possesses a fixed characteristic speed (which it must if a law of “least time” is to have any meaning), and that the speed is lower in more dense media (precisely opposite the view of Descartes and subsequently Newton and Maupertuis). Furthermore, applying the principle of least time rather than least distance to the law of propagation of light clearly casts the propagation of light into the arena of four-dimensional spacetime, and it essentially amounts to an assertion that the laws of motion should be geodesic paths with a suitable spacetime metric. Thus, Fermat's optical principle can be seen as a remarkable premonition of important elements of both special and general relativity.

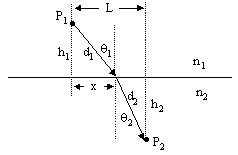
To derive the law of refraction for a ray of light traveling through the boundary between two homogeneous media, Fermat argued that a ray traveling from point 1 to point 2 in the figure below would follow the path that minimized the total time of the journey.

Letting v₁ denote the speed of light in medium 1, and v₂ denote the speed of light in medium 2, the total time of the journey is d₁/v₁ + d₂/v₂, which can be written in terms of the unknown x as

Differentiating with respect to x gives

Setting this to zero gives the relation

which is equivalent to Snell's law n₁sin(θ₁) = n₂ sin(θ₂) provided we assume the refractive index of a medium is proportional to the inverse of the velocity of light in that medium. Since calculus hadn't been invented yet, Fermat's solution of the problem involved considerably more labor (and ingenuity) than shown above, but eventually he arrived at this result, which surprisingly was experimentally indistinguishable from the formula arising from Descartes' derivation, despite the fact that the latter was based on an opposite set of assumptions, namely, that the velocity (or the "force") of light in a given medium is directly proportional to the refractive index of that medium!

It may seem strange that two opposite hypotheses as to the speed of light should lead to the same empirical result, but in fact without the ability to directly measure the speed of light in various media we cannot tell from the refractivities of materials whether the index is proportional to velocity or to the reciprocal of velocity. Even though both assumptions lead to the same law of refraction, the dispute over the correct derivation of this law continued unabated, because each side regarded the other side's interpretation as a travesty of science. Among those who believed light travels faster in denser media are Hooke and Newton, whereas Huygens derived the law of refraction based on his wave theory of light (see Section 8.9) and concluded that Fermat's hypothesis was correct, i.e., the speed of light was less in denser media.

More than a century later (around 1747) Maupertuis applied his "principle of least action" to give an elegant (albeit spurious) derivation of Snell's law from the hypothesis that light travels faster in denser media. Maupertuis believed that the wisdom and economy of God is manifest in all the operations of nature, which necessarily proceed from start to finish in just such a way as to minimize the "quantity of action". In a sense, this is closely akin to Fermat's principle of least time, since they are both primitive examples of what we would now call the calculus of variations. However, Maupertuis developed an all-encompassing view of his "least action" principle, with mystical and religious implications, and he argued that it was the universal governing principle in all areas of physics, including mechanics, optics, thermodynamics, and all other natural processes.

Of course, the notion that the phenomena of nature must follow the "best possible" course was not new. For example, as discussed in Section 8.2, Plato's Phaedo quotes Socrates as saying “If one wished to know the cause of each thing... one had to find what was the best way for it to be, or to be acted upon, or to act.”. The innovation of Maupertuis was to suggest a quantitative measure for the vague notion of "what is best" for physical processes, and to demonstrate that this kind of reasoning can produce valid quantitative results in a wide range of applications. His proposal was to minimize the product of mass, velocity, and displacement. (Subsequently Lagrange clarified this by defining the action of a system as the spatial path integral of the product of mass and velocity.) For a system whose mass does not change, Maupertuis regarded the action as simply proportional to the product of velocity and distance traveled. To derive the law of refraction for a ray of light traveling through the boundary between two homogeneous media, Maupertuis argued that a ray traveling from point 1 to point 2 in the figure above would follow the path that minimized the total "action" v₁d₁ + v₂d₂ of the journey. This is identical to the quantity that Fermat minimized, except that the speeds appear in place of their reciprocals. Since v₁ and v₂ are constants, the differentiation proceeds as before, except for the inverted speed constants, and Maupertuis arrives at the relation

which would be equivalent to Snell's law n₁sin(θ₁) = n₂ sin(θ₂) if we assumed the refractive index of a medium was proportional to the velocity of light in that medium, more or less consistent with the views of Descartes, Hooke, Newton. Since the deviation of the refractive index from unity is known empirically to be roughly proportional to the density of the medium, this would imply that light travels faster in denser media, which Newton and the others found quite plausible. (Newton derives this relation for a corpuscular theory of light in Proposition 95 of Book 1 of his Principia, and discusses it further in Proposition 6 of Book 1 of his Opticks.)

No amount of experimenting with the relative refractions of various media would suffice to distinguish between these two possibilities (the refractive index being proportional to the velocity or the reciprocal velocity). Only a direct measurement of the speed of light in two media with different refractive indices could accomplish this. Such a measurement was not achieved until 1850, when Focault passed rays of light through a tube, and by using a rapidly rotating mirror was able to show conclusively that light takes longer to traverse the tube when it is filled with water than when filled with air. So, after 200 years of theorizing and speculation, the question was finally settled in favor of Fermat and Huygens, i.e., the index of refraction is inversely proportional to the speed of light in the medium.

It's worth noting that although Fermat was closer to the truth, his principle of "least time" is not strictly correct, because the modern formulation of "Fermat's Principle" states that light travels along a path for which the time is stationary, (i.e., such that slight transverse changes in the path don't affect its length), not necessarily minimal. In fact, it may even be maximal, as can be verified by looking at yourself in the concave surface of a shiny spoon. The "reason" that light prefers stationary paths can be found in the theory of quantum electrodynamics and Feynman's "sum over all paths" interpretation (closely related to Huygens’ Principle), which shows that if neighboring paths take different amounts of time, the neighboring rays arrive at the destination out of phase, and cancel each other out, whereas they reinforce each other if the neighboring paths take the same amount of time, or differ by some whole multiple of the wave. A stark demonstration of this is given by diffraction gratings, in which the canceling regions of a mirror are scraped away, resulting in reflective properties that violate Hero's law of equal angles. (See Section 8.11.)

The modified version of Fermat’s Principle (requiring stationary rather than minimal paths) has proven to be a remarkably useful approach to the formulation of all kinds of physical problems involving motion and change. Also, subsequent optical experiments confirmed Fermat’s intuition that the index of refraction for a given medium was inversely proportional to the (phase) velocity v of light in the medium. The modern definition of the refractive index is n = c/v, where the constant of proportionality c is the speed of light in a vacuum. As an aside, the fact Newton’s particle theory and Huygens’ wave theory are both consistent with the same law of refraction, even though one implies the index of refraction is proportional to v while the other implies that it is proportional to 1/v, may be less surprising when we recall that this is a symmetry of the relativistic velocity-composition law as described in Section 1.8, and that it is also the relation between phase and group velocity of a matter wave in quantum theory.

In any case, it's clear that Fermat's model of optics based on his principle of least time, when interpreted as a metrical theory, entails or suggests many of the important elements of the modern theory of relativity, including the fundamental assumption of a characteristic speed of light for each medium, the concept of a unified space-time as the effective arena of motion, and the assumption that natural motions follow geodesic paths.

Return to Table of Contents