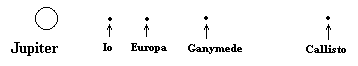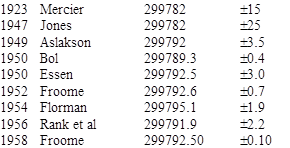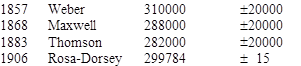3.3  De Mora Luminis

I see my light come shining,

From the west down to the east.

Any day now, any day now,

I shall be released.

         Bob Dylan, 1967

We are usually not aware of any delay between the occurrence of an event and its visual appearance in the eye of a distant observer. In fact, a single visual "snapshot" is probably the basis for most people's intuitive notion of an "instant". However, the causal direction of an instantaneous interaction is inherently ambiguous, so it's perhaps not surprising that ancient scholars considered two competing models of vision, one based on the idea that every object is the source of images of itself, emanating outwards to the eye of the observer, and the other claiming that the observer's eye is the source of visual rays emanating outwards to "feel" distant objects. An interesting synthesis of these two concepts is the idea, adopted by Descartes, of light as a kind of pressure in an ideal incompressible medium that conveys forces and pressures instantaneously from one location to another. However, even with Descartes we find the medium described as "incompressible, or nearly incompressible", revealing the difficulty of reconciling instantaneous force at a distance with our intuitive idea of causality. Fermat raised this very objection when he noted (in a letter on Descartes' Dipotrics) that if we assume instantaneous transmission of light we are hardly justified in analyzing such transmissions by means of analogies with motion through time.

Perhaps urged by the sense that any causal action imposed from one location on another must involve a progression in time, many people throughout history have speculated that light may propagate at a finite speed, but all efforts to discern a delay in the passage of light (mora luminus) failed. One of the earliest such attempts of which we have a written account is the experiment proposed by Galileo, who suggested (in his Dialogue Concerning Two New Sciences) relaying a signal back and forth with lamps and shutters located on separate hilltops. Based on the negative results from this type of crude experiment, Galileo could only confirm what everyone already knew, namely, that the propagation of light is "if not instantaneous, then extraordinarily fast". He went on to suggest that it might be possible to discern, in distant clouds, some propagation time for the light emitted by a lightning flash.

We see the beginning of this light – I might say its head and source – located at a particular place among the clouds; but it immediately spreads to the surrounding ones, which seems to be an argument that at least some time is required for propagation. For if the illumination were instantaneous and not gradual, we should not be able to distinguish its origin – its center, so to speak – from its outlying portions.

The idea of using the clouds in the night sky as a giant bubble chamber was characteristic of Galileo’s talent for identifying opportunities in natural phenomena for testing ideas, as well as his attentiveness to subtle qualitative impressions, such as the sense of being able to distinguish the “center” of the illumination given off by a flash of lightning, even though we can’t quantify the delay time. It also shows that Galileo was inclined to think light propagated at a finite speed, but of course he rightly qualified this lightning-cloud argument by admitting that “really these matters lie far beyond our grasp”. Today we would say the perceived “spreading out” of a lightning strike through the clouds is due to propagation of the electrical discharge process. Even for clouds located ten miles apart, the time for light itself to propagate from one cloud to the other is only one 18,600th of a second, presumably much too short to give any impression of delay to human senses.

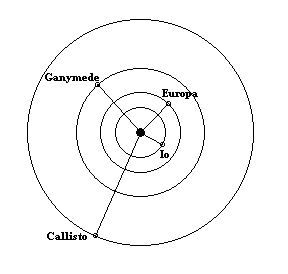
Interestingly, Galileo also contributed (posthumously) to the first successful attempt to actually observe a delay attributable to the propagation of light at a finite speed. In 1610, soon after the invention of the telescope, he discovered the four largest moons of Jupiter, illustrated below:

In hopes of gaining the patronage of the Grand Duke Cosimo II, Galileo named Jupiter's four largest moons the "Medicean Stars", but today they're more commonly called the Galilean satellites. At their brightest these moons would be just bright enough (with magnitudes between 5 and 6) to be visible from Earth with the naked eye - except that they are normally obscured by the brightness of Jupiter itself. (Interestingly, there is some controversial evidence suggesting that an ancient Chinese astronomer may actually have glimpsed one of these moons 2000 years before Galileo.) Of course, from our vantage point on Earth, we must view the Jupiter system edgewise, so the moons appear as small stars that oscillate from side to side along the equatorial plane of Jupiter. If they were all perpendicular to the Earth's line of sight, and all on the same side of Jupiter, simultaneously, they would look like this:

By the 1660's, detailed tables of the movements of these moons had been developed by Borelli (1665) and Cassini (1668). Naturally these tables were based mainly on observations taken around the time when Jupiter is nearly "in opposition", which is to say, when the Earth passes directly between Jupiter and the Sun, because this is when Jupiter appears high in the night sky. The mean orbital periods of Jupiter's four largest moons were found to be 1.769 days, 3.551 days, 7.155 days, and 16.689 days, and these are very constant and predictable (especially for the two inner moons), like a giant clockwork. (In fact, there were serious attempts in the 18th century to develop a system of tables and optical instruments so that the "Jupiter clock" could be used by sailors at sea to determine Greenwich Meridian time, from which they could infer their longitude.) Based on these figures it was possible to predict within minutes the times of eclipses and passages (i.e., the passings behind and in front of Jupiter) that would occur during the viewing opportunities in future "oppositions". In particular, the innermost satellite, Io (which is just slightly larger than our own Moon), completes one revolution around Jupiter every 42.456 hours. Therefore, when viewed from the Earth, we expect to see Io pass behind Jupiter once every 42 hours, 27 minutes, and 21 seconds - assuming the light from each such eclipse takes the same amount of time to reach the Earth.

By the 1670's people began to make observations of Jupiter's moons from the opposite side of the Earth's orbit, i.e., when the Earth was on the opposite side of the Sun from Jupiter, and they observed a puzzling phenomenon. Obviously it's more difficult to make measurements at these times, because the Jovian system is nearly in conjunction with the Sun, but at dawn and dusk it is possible to observe Jupiter even when it is fairly close to conjunction. These observations, taken about 6 months away from the optimum viewing times, reveal that the eclipses and passages of Jupiter's innermost moon, Io, which could be predicted so precisely when Jupiter is in opposition, are consistently late by about 17 minutes relative to their predicted times of occurrence. (Actually the first such estimate, made by the Danish astronomer Ole Roemer in 1675, was 22 minutes.) This is not to say that the time intervals between successive eclipses is increased by 17 minutes, but that the absolute time of occurrence is 17 minutes later than was predicted six months earlier based on the observed orbital period at that time. Since Io has a period of 1.769 days, it completes about 103 orbits in six months, and it appears to lose a total of 17 minutes during those 103 orbits, which is an average of about 9.9 seconds per orbit.

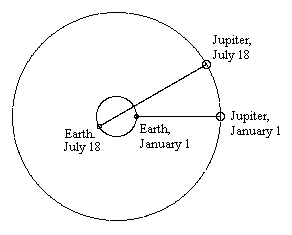
Nevertheless, at the subsequent "opposition" viewing six months later, Io is found to be back on schedule! It's as if a clock runs slow for half the year and fast for the other half, so that on average it keeps perfect time over the years. While mulling over this data in 1675, it occurred to Roemer that he could account for the observations perfectly if it is assumed that light propagates at a finite speed. At last someone had observed the mora luminus. Light travels at a finite speed, which implies that when we see things we are really seeing how they were at some time in the past. The further away we are from an object, the greater the time delay in our view of that object. Applying this hypothesis to the observations of Jupiter's moons, Roemer considered the case when Jupiter was in opposition on, say, January 1, so the light from the Jovian eclipses was traveling from the orbit of Jupiter to the orbit of the Earth, as shown in the figure below.

The intervals between successive eclipses around this time will be very uniform near the opposition point, because the eclipses themselves are uniform and the distance from Jupiter to the Earth is fairly constant during this time. However, after about six and a half months (denoted by July 18 in the figure), Jupiter is in conjunction, which means the Earth is on the opposite side of it's orbit from Jupiter. The light from the "July 18" eclipse will still cross the Earth's orbit (on the near side) at the expected time, but it must then travel an additional distance, equal to the diameter of the Earth's orbit, in order to reach the Earth. Hence we should expect it to be "late" by the amount of time required for light to travel the Earth's orbital diameter. Combining this with a rough estimate of the distance from the Earth to the Sun, Huygens reckoned that light must travel at about 209,000 km/sec. A subsequent estimate by Newton gave a value around 241,000 km/sec. In fact, the Scholium to Proposition 96 of Newton's Principia includes the statement

For it is now certain from the phenomenon of Jupiter's satellites, confirmed by the observations of different astronomers, that light is propagated in succession, and requires about seven or eight minutes to travel from the sun to the earth.

The early quantitative estimates of the speed of light were obviously impaired by the lack of precise knowledge of the Earth-Sun distance. Using modern techniques, the Earth's orbital diameter is estimated to be about 2.98 x 10¹¹ meters, and the observed time delay in the eclipses and passages of Jupiter's moons when viewed from the Earth with Jupiter in conjunction is about 16.55 minutes = 993 seconds, so we can deduce from these observations that the speed of light is about 2.98 x 10¹¹ / 993  »  3 x 10⁸ meters/sec.

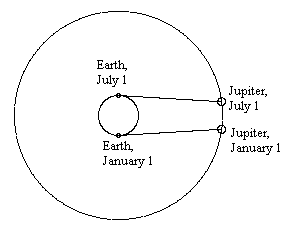
Of course, Roemer's hypothesis implies a specific time delay for each point of the orbit, so it can be corroborated by making observations throughout the year. We find that most of the discrepancy occurs during the times when the distance between Jupiter and the Earth is changing most rapidly, which is when the Earth-Sun axis is nearly perpendicular to the Jupiter-Sun axis. At one of these positions the Earth is moving almost directly toward Jupiter, and at the other it is moving almost directly away from Jupiter, as shown in the figure below.

The Earth's speed relative to Jupiter at these points is essentially just its orbital speed, which is the circumference of its orbit divided by one year. Thus we have

which is equivalent to about 3 x 10⁴ meters/sec. If we choose units so that c = 1, then we have v = 0.0001. From this point of view the situation can be seen as a simple application of the Doppler effect, and the frequency of the eclipses as viewed on Earth can be related to the actual frequency (which is what we observe at conjunction and opposition) according to the formulas

The frequencies are inversely proportional to the time intervals between eclipses. These formulas imply that, for the moon Io, whose orbital period is 1.769 days = 2547.3600 minutes, the time interval between consecutive observed eclipses when the Earth is moving directly toward Jupiter (indicated as "Jan" in the above figure) is 2547.1052 minutes, and the time intervals between successive observed eclipses six months later is 2547.6147 minutes. Thus the interval between observed eclipses is 15.2 seconds shorter than nominal in the former case, and it is 15.3 seconds longer than nominal in the latter case, making a total difference of 30.5 seconds between the inter-arrival times at the two extremes, separated by six months. It would have been difficult to keep time this accurately in Roemer's day, but differences of this size are easily measured with modern clocks. By the way, the other moons of Jupiter do not conform so nicely to Roemer's hypothesis, but this is because their orbital motions are inherently more irregular due to their mutual gravitational interactions.

Despite the force of Roemer's analysis, and the early support of both Huygens and Newton, most scientists remained skeptical of the idea of a finite speed of light. It was not until 50 years later, when the speed of light was evaluated in a completely different way, arriving at nearly the same value, that the idea became widely accepted. This occurred in 1729, when the velocity of light was estimated by James Bradley based on observations of the aberration of starlight, which he argued must depend on the ratio of the speed of light to the orbital speed of the Earth. Based on the best measurements of the limiting starlight aberration 20.4" ± 0.1" by Otto Struve, and taking the speed of the Earth to be about 30.56 km/sec from Encke's solar parallax estimate of 8.57" ± 0.04", this implied a light speed of about 308,000 km/sec.

Unfortunately, Encke's parallax estimates had serious problems, and he greatly under-estimated his error band. The determination of the Earth-Sun distance was a major challenge for scientists in the 18th century. Interestingly, the primary mission of Captain James Cook when he embarked in the ship Endeavour on his famous voyage in 1768 was to observe the transit of the planet Venus across the disk of the Sun from the vantage point of Tahiti in the South seas, with the aim of determining the distance from the Sun to the Earth by parallax. Roughly once each century two such conjunctions are visible from the Earth, occurring eight years apart. Edmund Halley had urged that when the next opportunities arose on June 6, 1761, and June 3, 1769, it be observed from as many vantage points as possible on the Earth's surface to make the best possible determination. The project was undertaken by people from many countries. Le Gentil traveled to India for the 1761 transit, but since England and France were antagonists at the time, he had to dodge the English war ships, causing him to reach India just after June 6, missing the first transit of Venus. Determined not to miss the second one, he remained in India for the next eight years (!) "doing various useful work" (according to Pannekoek) until June 3 1769. Alas, when the day arrived, it was too cloudy to see anything.

Cook's observations fared somewhat better. The French government actually issued orders to its war ships to leave Cook alone, since he was "on a mission for the benefit of all mankind". The Endeavour arrived in Tahiti on April 13, 1769, and the scientists were able to make observations in the clear on June 3. Unfortunately, the results were disappointing, not only in Tahiti, but all over the world. It turned out to be extremely difficult to judge precisely (to within, say, 10 seconds) when one edge of Venus passed the border of the Sun. The black disk of the planet appeared to "remain connected like a droplet" to the border of the Sun, until suddenly the connection was broken and the planet was seen to be well past the border. Observers standing right next to each other recorded times differing by tens of seconds. Consequently the observations failed to yield an improved estimate of the Earth-Sun distance.

The first successful quantification of c based solely on terrestrial measurements was probably Fizeau's in 1849, using a toothed wheel, and then Foucault's experiment in 1862 using rotating mirrors. The toothed-wheel didn't work very well, and it was hard to say how accurate it was, but the rotating mirrors led to a value of about 298,000 ± 500 km/sec, significantly below the earlier estimates. Foucault was confident the discrepancy with earlier results couldn't be explained by an error in the aberration angle, so he inferred (correctly) that Encke's Solar parallax estimate (and therefore the orbital velocity of the Earth) was in error, and proposed a value of 8.8", which was subsequently confirmed and refined by new observations, as well as a re-analysis of Encke's 1769 data using better longitudes and yielding an estimate of 8.83".

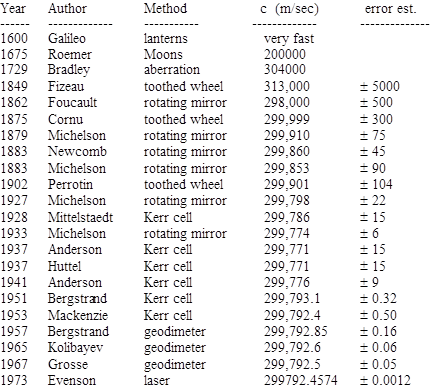
To increase the speed of switching the light signal, Kerr cells were used. These rely on the fact that the refractivity of certain substances can be made to vary with an applied electric voltage. Further refinements led to large-baseline devices, called geodimeters, originally intended for use in geodesic surveying. Here is a summary of the major published determinations of the speed of optical light based on one or another of these techniques:

Measurements of the speed of electromagnetic waves in the radio frequency have also been made, with the results summarized below:

In addition, the speed of light can be determined indirectly by measuring the ratio of electric to magnetic units, which amounts to measuring the permittivity of the vacuum. Some result given by this method are summarized below:

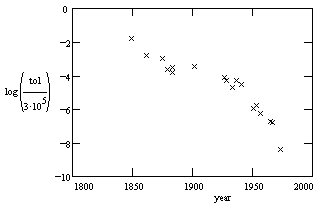
(Several of the above values include corrections for various group-velocity indices.) A plot of the common logarithm of the tolerance versus the year for the 19 optical light speed measurements is shown below:

Interestingly, comparing each of the measured values with Evenson's 1973 value, we find that more than half of them were in error by more than their published tolerances. This is not so surprising when we note that most of the tolerances were quoted as "one sigma" error bands rather than as absolute limits. Indeed, if we consider the two-sigma band, there were only four cases of over-optimism, and of those, all but Foucault's 1862 result are within three sigma, and even Foucault is within four sigma. This is roughly in agreement with what one would expect, especially for delicate and/or indirect measurements. Also, the aggressive error estimates in this field have had the beneficial effect of spurring controversies between different researchers, forcing them to repeat experiments and refine their techniques in order to resolve the disagreements. In this way, knowledge of the speed of light progressed in less than 400 years from Galileo's assessment, "extraordinarily fast", to the best modern value, 299,792.4574 ± 0.0012 km/sec. Today the unit of length is actually defined as a specific number of wavelengths of light of a certain frequency, based on the known value of the speed of light, so in effect we now define the meter such that the speed of light is exactly 299792.4574 km/sec.

Incidentally, Maxwell once suggested (in his article on Ether for the ninth edition of the Encyclopedia Britannica) that Roemer's method could be used to test for the isotropy of light speed, i.e., to test whether the speed of light is the same in all directions. After noting that any purely terrestrial measurement would yield an effect only of the second order in v/c, which he regarded as “quite insensible” (a remark that spurred Albert Michelson to successfully measure just such a quantity only two years later), he wrote

The only practicable method of determining directly the relative velocity of the aether with respect to the solar system is to compare the values of the velocity of light deduced from the observation of the eclipses of Jupiter's satellites when Jupiter is seen from the earth at nearly opposite points of the ecliptic.

Notice that, for this type of observation, the relevant speed is not the speed of the earth in its orbit around the sun, but rather the speed of the entire solar system. Roemer's method can be regarded as a means of measuring the speed of light in the direction from Jupiter to the Earth, and since Jupiter has an orbital period of about 12 years, we can use this method to evaluate the speed of light several times over a 12 year period, and thus evaluate the speed in all possible directions (in the plane of the ecliptic). If the sun was stationary, we would not expect to find any differences, but it was already suspected in Maxwell’s time that the sun itself is in motion. The best modern estimate is that our solar system is moving with a speed of about 3.7 x 10⁵ meters per second with respect to the cosmic microwave background radiation (i.e., the frame in which the radiation is roughly isotropic). If we assume a pre-relativistic model in which light propagates at a fixed speed with respect to the background radiation, and in which frames are related by Galilean transformations, we could in principle determine the "absolute speed" of the solar system. The magnitude of the effect is given by computing how much difference would be expected in the time for light to traverse one orbital diameter of the Earth at an effective speed of c+V and c-V, where V is the presumed absolute speed of the Earth. This gives a maximum difference of about 2.45 seconds between two measurements taken six years apart. (These two measurements each occur over a 6 month time span as explained above.)

Of course, like all purported “one-way” speed measurements, this method relies on an assumption about synchronization of clocks at different locations. In this case the procedure tacitly relies on the “slow clock transport” method of synchronization, as the clock on Earth is carried to different locations. We now know that slow clock transport yields the same result as both optical and mechanical synchronization, so this experiment would not be expected to yield any anisotropy – even if it could be carried out. In practice it would be necessary to account for many other uncontrolled variables, such as the variations in the orbits of the Earth and Jupiter over the six year interval. These would need to be known to much better than 1 part in 400 to give adequate resolution. To the best of my knowledge, this experiment has never been performed, because by the time sufficiently accurate clocks were available the issue of light's invariance with respect to inertial coordinate systems had already been established by more accurate terrestrial measurements, together with an improved understanding of the meaning of inertial coordinates. Today we are more likely to establish a system of coordinates optically, and then test to verify the isotropy of mechanical inertia with respect to those coordinates.

Return to Table of Contents