Postulates and Principles

3.1 Postulates and Principles

Complex ideas may perhaps be well known by definition, which is nothing but an enumeration of those parts or simple ideas that comprise them. But when we have pushed up definitions to the most simple ideas, and find still some ambiguity and obscurity, what resources are we then possessed of?

David Hume, 1748

We saw in Section 1.8 that, even after stipulating the existence of coordinate systems with respect to which inertia is homogeneous and isotropic, there remains a fundamental amgibuity as to the relationship between relatively moving inertial coordinate systems, corresponding to three classes of possible metrical structures with the k values -1, 0, and +1. There is a remarkably close historical analogy for this situation, dating back to one of the first formal systems of thought ever proposed. In Book I of The Elements, Euclid consolidated and systematized geometry as it was known circa 300 BC into a formal deductive system. As it has come down to us, it is based on five postulates together with several definitions and common notions. (It’s worth noting, however, that the classifications of these premises was revised many times in various translations.) The first four of these postulates are stated very succinctly

1. A straight line may be drawn from any point to any other point.

2. A straight line segment can be uniquely and indefinitely extended.

3. We may draw a circle of any radius about any point.

4. All right angles are equal to one another.

Strictly speaking, each of these seemingly simple assertions entails a fairly complicated set of premises and ambiguities, but they were generally accepted as unobjectionable. However, Euclid's final postulate has a very different appearance from the others - a difference that neither Euclid nor his subsequent editors and translators attempted to disguise – and it was regarded with suspicion from earliest times. The fifth postulate is expressed as follows:

5. If a straight line falling on two straight lines makes the [sum of the] interior angles on the same side less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.

This postulate is equivalent to the statement that there's exactly one line through a given point P parallel to a given line L, as illustrated below

Although this proposition is fairly plausible (albeit somewhat awkward to state), many people suspected that it might be logically deducible from the other postulates, axioms, and common notions. There were also attempts to substitute for Euclid's fifth postulate a simpler or more self-evident proposition. However, we now understand that Euclid's fifth postulate is logically independent of the rest of Euclid's logical structure. In fact, it's possible to develop logically consistent geometries in which Euclid's fifth postulate is false. For example, we can assume that there are infinitely many lines through P that are parallel to (i.e., never intersect) the line L. It might seem (at first) that it would be impossible to reason with such an assumption, that it would either lead to contradictions or else cause the system to degenerate into a logical triviality about which nothing interesting could be said, but, remarkably, this turns out not to be the case.

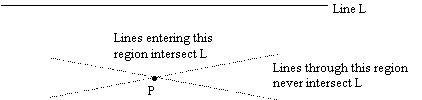
Suppose that although there are infinitely many lines through P that never intersect L, there are also infinitely many that do intersect L. This, combined with the other axioms and postulates of plane geometry, implies that there are two lines through P defining the boundary between lines that do intersect L and lines that don't, as shown below:

This leads to the original non-Euclidean geometry of Lobachevski, Bolyai, and Gauss, i.e., the hyperbolic plane. The analogy to Minkowski spacetime is obvious. The behavior of “straight lines” in a surface of negative curvature (although positive-definite) is nicely suggestive of how the light-lines in spacetime serve as the dividing lines between those lines through P that intersect with the future "L" and those that don't (distinguishing between spacelike and timelike intervals). This is also a nice illustration of the fact that even though Minkowski spacetime is "flat" in the Riemannian sense, it is nevertheless distinctly non-Euclidean. Of course, the possibility that spacetime might be curved as well as locally Minkowskian led to general relativity, but arguably the conceptual leap required to go from a positive-definite to a non-positive-definite metric is greater than that required to go from a flat to a curved metric. The former implies that the local geometrical structure of the effective spatio-temporal manifold of events is profoundly different than had been assumed for thousands of years, and this realization led naturally to a new set of principles with which to organize and interpret our experience.

It became clear in the nineteenth century that there are actually three classes of geometries consistent with Euclid’s basic premises, depending on what we adopt as the “fifth postulate”. The three types of geometry correspond to spaces of negative, positive, or zero curvature. The analogy to the three possible classes of spacetimes (Euclidean, Galilean, and Minkowskian) is obvious, and in both cases it came to be recognized that, insofar as these mathematical structures were supposed to represent physical properties, the choice between the alternatives was a matter for empirical investigation.

Nevertheless, the superficially axiomatic way in which Einstein presented the special theory in his 1905 paper tended to encourage the idea that special relativity represented a closed formal system, like Euclid’s geometry interpreted in the purely mathematical sense. For example, in 1907 Paul Ehrenfest wrote that

In the formulation in which Mr Einstein published it, Lorentzian relativistic electrodynamics is rather generally viewed as a complete system. Accordingly it must be able to provide an answer purely deductively to the question [involving the shape of the moving electron]…

Einstein himself was quick to disavow this idea, answering

The principle of relativity, or, more exactly, the principle of relativity together with the principle of the constancy of the velocity of light, is not to be conceived as a “complete system,” in fact, not as a system at all, but merely as a heuristic principle which, when considered by itself, contains only statements about rigid bodies, clocks, and light signals. It is only by requiring relations between otherwise seemingly unrelated laws that the theory of relativity provides additional statements.

Just as the basic premises of Euclid’s geometry were classified in many different ways (e.g., postulates, axioms, common notions, definitions), the premises on which Einstein based special relativity can be classified in many different ways. Indeed, in his 1905 paper, Einstein introduced the first of these premises as follows:

... the same laws of electrodynamics and optics will be valid for all coordinate systems in which the equations of mechanics hold good. We will raise this conjecture (hereafter called the "principle of relativity") to the status of a postulate...

Here, in a single sentence, we find a proposition referred to as a conjecture, a principle, and a postulate. The meanings of these three terms are quite distinct, but they are each arguably applicable. The assertion of the co-relativity of optics and mechanics was, and will always be, conjectural, because it can be empirically corroborated only up to a limited precision. Einstein formally adopted this conjecture as a postulate, but on a more fundamental level it serves as a principle, since it entails the decision to organize our knowledge in terms of coordinate systems with respect to which the equations of mechanics hold good, i.e., inertial coordinate systems. Einstein goes on to introduce a second proposition that he formally adopts as a postulate, namely,

... that the velocity of light always propagates in empty space with a definite velocity c that is independent of the state of motion of the emitting body. These two postulates suffice for the attainment of a simple and consistent electrodynamics of moving bodies based on Maxwell's theory for bodies at rest.

In the more precise statement of this principle later in the paper, Einstein actually asserts it for just one specific system of inertial coordinates (the “stationary” system), and then states that this proposition, combined with the relativity principle, implies that light must propagate at c in terms of every inertial system. However, the crucial phrase “in empty space” tacitly assumes that there is such a thing as empty space, and that light propagates in it, and that it is completely indifferent to states of motion, which amounts to simply positing that light (in empty space) has the same speed in every inertia-based coordinate system. This is why many later expositions omit Einstein’s maneuver and simply assert the stronger statement as the principle, rather than claiming to derive it.

Interestingly, in the paper "Does the Inertia of a Body Depend on Its Energy Content?" published later in the same year, Einstein commented that

... the principle of the constancy of the velocity of light... is of course contained in Maxwell's equations.

In view of this, some have wondered why in his axiomatic foundations he did not simply dispense with his "light speed postulate”, and assert that the "laws of electrodynamics and optics" in the statement of the first principle are none other than Maxwell's equations, from which (suitably interpreted) the constancy of the speed of light follows. In other words, why didn’t he simply base his theory on the single proposition that Maxwell's equations are valid for every system of coordinates in terms of which the laws of mechanics hold good? The answer, of course, is that the relativity principle does not entail a commitment to any particular set of physical laws, either of mechanics or of electrodynamics. Any such commitment would represent additional postulates. The relativity principle merely asserts that the laws of mechanics and electrodynamics (and everything else), whatever those laws may be, are equally applicable in terms of any system of inertial coordinates. This statement no more entails the acceptance of Maxwell’s equations of electromagnetism than it does Newton’s equations of mechanics. Indeed, not only does special relativity require a modification of Newtonian mechanics, it was also clear to Einstein in 1905 that Maxwell’s equations could not claim unlimited validity. In his paper "On a Heuristic Point of View Concerning the Production and Transformation of Light" he wrote

... despite the complete confirmation of [Maxwell's theory] by experiment, the theory of light, operating with continuous spatial functions, leads to contradictions when applied to the phenomena of emission and transformation of light.

Furthermore, he knew that important parts of physics, such as the physics of elementary particles, cannot possibly be explained in terms of Maxwellian electrodynamics. For example, in a note published in 1907 he wrote

It should be noted that the laws that govern [the structure of the electron] cannot be derived from electrodynamics alone. After all, this structure necessarily results from the introduction of forces which balance the electrodynamic ones.

Thus it isn't surprising that he chose not to base the theory of relativity on Maxwell’s equations, especially since, far from reducing the number of postulates, it would greatly increase the number of postulates, because Maxwell’s equations entail far more than just the invariance of light speed. Nevertheless, some additional principle is needed to supplement the relativity principle and pick out the specific kind of relativity (Galilean, Lorentzian, or Euclidean) that applies to space-time phenomena. Einstein distilled from electrodynamics the key feature which could claim (he surmised) unlimited validity, and whose significance "transcended its connection with Maxwell's equations", and which would serve as a viable principle for organizing our knowledge of all phenomena, including not only electrodynamics, optics, and mechanics, but also the (then) unknown laws that govern the structure of the electron. The principle he selected was essentially the existence of an invariant speed with respect to any (local) system of inertial coordinates. For definiteness he identified this speed with the speed of propagation of electromagnetic energy (or any energy with zero rest mass).

After reviewing the operational definition of inertial coordinates in section §1 (which he does by optical rather than mechanical means, thereby missing an opportunity to clarify the significance of inertial coordinates in establishing the connection between mechanical and optical phenomena), he gives more formal statements of his two principles

The following reflections are based on the principle of relativity and the principle of the constancy of the velocity of light. These two principles we define as follows:

1. The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion.

2. Any ray of light moves in the "stationary" system of co-ordinates with the determined velocity c, whether the ray is emitted by a stationary or by a moving body. Hence velocity equals [length of] light path divided by time interval [of light path], where time interval [and length are] to be taken in the sense of the definition in §1.

The first of these is nothing but the principle of inertial relativity, which had been accepted as a fundamental principle of physics since the time of Galileo (see section 1.3). Strictly speaking, Einstein’s statement of the principle here is incorrect, because he assumes the coordinate systems in which the equations of mechanics hold good are fully characterized by being in uniform translatory motion, whereas in fact it is also necessary to specify an inertially isotropic simultaneity. Einstein chose to address this aspect of inertial coordinate systems by means of a separate and seemingly discretionary definition of simultaneity based on optical phenomena, which unfortunately has invited much misguided philosophical debate about what should be considered “true” simultaneity. All this could have been avoided if, from the start, Einstein had merely stated that an inertial coordinate system is one in which mechanical inertia is homogeneous and isotropic (just as Galileo said), and then noting that this automatically entails the conventional choice of simultaneity. The content of his first principle (i.e., the relativity principle) is simply that the inertial simultaneity of mechanics and the optical simultaneity of electrodynamics are identical.

Despite the shortcomings of its statement, the principle of relativity was very familiar to the physicists of 1905, whether they wholeheartedly accepted it or not. Einstein's second principle, by itself, was also not regarded as particularly novel, because it conveys the usual understanding of how a wave propagates at a fixed speed through a medium, independent of the speed of the source. It was the combination of these two principles that was new, since they had previously been considered irreconcilable. In a sense, the first principle arose from the “ballistic particles in a vacuum” view of physics, and the second arose from the “wave in a material medium” view of physics. Both of these views can trace their origins back to ancient times, and both seem to capture some fundamental truth about the world, and yet they had always been regarded as mutually exclusive. Einstein’s achievement was to explain how they could be reconciled.

Of course, Einstein’s second principle it isn't a self-contained statement, because its entire meaning and significance depends on "the sense of" time intervals and (implicitly) spatial lengths given in §1, where we find that time intervals and spatial lengths are defined to be such that their ratio equals the fixed constant c for light paths. This has tempted some readers to conclude that "Einstein's second principle" was merely a tautology, with no substantial content. The source of this confusion is the fact that the essential axiomatic foundations underlying special relativity are contained not in the two famous propositions at the beginning of §2 of Einstein's paper (as quoted above), but rather in the sequence of assumptions and definitions explicitly spelled out in §1. Among these are the very first statement

Let us take a system of co-ordinates in which the equations of Newtonian mechanics hold good.

In subsequent re-prints of this paper Sommerfeld added a footnote to this statement, to say "i.e., to the first approximation", meaning for motion with speeds small in comparison with the speed of light. (This illustrates the difficulty of writing a paper that results in a modification of the equations of Newtonian mechanics!) Of course, Einstein was aware of the epistemological shortcomings of the above statement, because while it tells us to begin with an inertial system of coordinates, it doesn't tell us how to identify such a system. This has always been a potential source of ambiguity for mechanics based on the principle of inertia. Strictly speaking, Newton's laws are epistemologically circular, so in practice we must apply it both inductively and deductively. First we use them inductively with our primitive observations to identify inertial coordinate systems by observing how things behave. Then at some point when we've gained confidence in the inertialness of our coordinates, we begin to apply the laws deductively, i.e., we begin to deduce how things will behave with respect to our inertial coordinates. Ultimately this is how all physical theories are applied, first inductively as an organizing principle for our observations, and then deductively as "laws" to make predictions. Neither Galilean nor special relativity is able to justify the privileged role given to a particular class of coordinate systems, nor to provide a non-circular means of identifying those systems. In practice we identify inertial systems by means of an incomplete induction. Although Einstein was aware of the deficiency of this approach (which he subsequently labored to eliminate from the general theory), in 1905 he judged it to be the only pragmatic way forward.

The next fundamental assertion in §1 of Einstein's paper is that lengths and time intervals can be measured by (and expressed in terms of) a set of primitive elements called "measuring rods" and "clocks". As discussed in Section 1.2, Einstein was fully aware of the weakness in this approach, noting that “strictly speaking, measuring rods and clocks should emerge as solutions of the basic equations”, not as primitive conceptions. Nevertheless

it was better to admit such inconsistency - with the obligation, however, of eliminating it at a later stage of the theory...

Thus the introduction of clocks and rulers as primitive entities was another pragmatic concession, and one that Einstein realized was not strictly justifiable on any other grounds than provisional expediency.

Next Einstein acknowledges that we could content ourselves to time events by using an observer located at the origin of the coordinate system, which corresponds to the absolute time of Lorentz, as discussed in Section 1.6. Following this he describes the "much more practical arrangement" based on the reciprocal operational definition of simultaneity. He says

We assume this definition of synchronization to be free of any possible contradictions, applicable to arbitrarily many points, and that the following relations are universally valid:

1. If the clock at B synchronizes with the clock at A, the clock at A synchronizes with the clock at B.

2. If the clock at A synchronizes with the clock at B and also with the clock at C, the clocks at B and C also synchronize with each other.

These are important and non-trivial assumptions about the viability of the proposed operational procedure for synchronizing clocks, but they are only indirectly invoked by the reference to "the sense of time intervals" in the statement of Einstein's second principle. Furthermore, as mentioned in Section 1.6, Einstein himself subsequently identified at least three more assumptions (homogeneity, spatial isotropy, memorylessness) that are tacitly invoked in the formal development of special relativity. The list of unstated assumptions would actually be even longer if we were to construct a theory beginning from nothing but an individual's primitive sense perceptions. The justification for leaving them out of a scientific paper is that these can mostly be classified as what Euclid called "common notions", i.e., axioms that are common to all fields of thought.

In many respects Einstein modeled his presentation of special relativity not on Euclid’s Elements (as Newton had done in the Principia), but on the formal theory of thermodynamics, which is founded on the principle of the conservation of energy. There are different kinds of energy, with formally different units, e.g., mechanical and gravitational potential energy are typically measured in terms of joules (a force times a distance, or equivalently a mass times a squared velocity), whereas heat energy is measured in calories (the amount of heat required to raise the temperature of 1 gram of water by one degree C). It's far from obvious that these two things can be treated as different aspects of the same thing, i.e., energy. However, through careful experiments and observations we find that whenever mechanical energy is dissipated by friction (or any other dissipative process), the amount of heat produced is proportional to the amount of mechanical energy dissipated. Conversely, whenever heat is involved in a process that yields mechanical work, the heat content is reduced in proportion to the amount of work produced. In both cases the constant of proportionality is found to be 4.1833 joules per calorie.

Now, the First Law of thermodynamics asserts that the total energy of any physical process is always conserved, provided we "correctly" account for everything. Of course, in order for this assertion to even make sense we need to define the proportionality constants between different kinds of energy, and those constants are naturally defined so as to make the First Law true. In other words, we determine the proportionality between heat and mechanical work by observing these quantities and assuming that those two changes represent equal quantities of something called "energy". But this assumption is essentially equivalent to the First Law, so if we apply these operational definitions and constants of proportionality, the conservation of energy can be regarded as a tautology or a convention.

This shows clearly that, just as in the case of Newton's laws, these propositions are actually principles rather than postulates, meaning that they first serve as organizing principles for our measurements and observations, and only subsequently do they serve as "laws" from which we may deduce further consequences. This is the sense in which fundamental physical principles always operate. Wein's letter of 1912 nominating Einstein and Lorentz for the Nobel prize commented on this same point, saying that "the confirmation of [special relativity] by experiment... resembles the experimental confirmation of the conservation of energy". Ineed, Einstein himself acknowledged that he consciously modeled the formal structure of special relativity on thermodynamics. He wrote in his autobiographical notes

The example I saw before me was thermodynamics. The general principle was there given in the proposition: The laws of nature are such that it is impossible to construct a perpetuum mobile (of the first and second kinds)… The universal principle of the special theory of relativity is contained in the postulate: The laws of physics are invariant with respect to Lorentz transformations (for the transition from one inertial system to any other arbitrarily chosen inertial system). This is a restricting principle for natural laws, comparable to the restricting principle of the nonexistence of the perpetuum mobile that underlies thermodynamics.

This principle is a meta-law, i.e., it does not express a particular law of nature, but rather a general principle to which all the laws of nature conform. As mentioned above, when Ehrenfest suggested that special relativity constituted a closed axiomatic system, Einstein quickly replied that the relativity principle combined with the principle of invariant light speed is not a closed system at all, but rather it provides a coherent framework within which to conduct physical investigations. As he put it, the principles of special relativity "permit certain laws to be traced back to one another (like the second law of thermodynamics)."

Not only is there a close formal similarity between the axiomatic structures of thermodynamics and special relativity, each based on two fundamental principles, these two theories are also substantively extensions of each other. The first law of thermodynamics can be placed in correspondence with the basic principle of relativity, which suggests the famous relation E = mc², thereby enlarging the realm of applicability of the first law. The second law of thermodynamics, like Einstein's second principle of invariant light speed, is more sophisticated and more subtle. A physical process whose net effect is to remove heat from a body and produce an equivalent amount of work is called perpetual motion of the second kind. It isn't obvious from the first law that such a process is impossible, and indeed there were many attempts to find such a process - just as there were attempts to identify the rest frame of the electromagnetic ether - but all such attempts failed. Moreover, they failed in such a way as to make it clear that the failures were not accidental, but that a fundamental principle was involved.

In the case of thermodynamics this was ultimately formulated as the second law, one statement of which (as alluded to by Einstein in the quote above) is simply that perpetual motion of the second kind is impossible - provided the various kinds of energy are defined and measured in the prescribed way. (This theory was Einstein's bread and butter, not only because most of his scientific work prior to 1905 had been in the field of thermodynamics, but also because a patent examiner inevitably is called upon to apply the first and second laws to the analysis of hopeful patent applications.) Compare this with Einstein's second principle, which essentially asserts that it's impossible to measure a speed in excess of the constant c - provided the space and time intervals are defined and measured in the prescribed way. The strength of both principles is due ultimately to the consistency and coherence of the ways in which they propose to analyze the processes of nature.

Needless to say, our physical principles are not arbitrarily selected assumptions, they are hard-won distillations of a wide range of empirical facts. Regarding the justification for the principles on which Einstein based special relativity, many popular accounts give a prominent place to the famous experiments of Michelson and Morley, especially the crucial version performed in 1889, often presenting this as the "brute fact" that precipitated relativity. Why, then, does Einstein’s 1905 paper fail to cite this famous experiment? It does mention at one point “the various unsuccessful attempts to measure the Earth’s motion with respect to the ether”, but never refers to Michelson's results specifically. The conspicuous absence of any reference to this important experimental result has puzzled biographers and historians of science. Clearly Einstein’s intent was to present the most persuasive possible case for the relativity of space and time, and Michelson's results would (it seems) have been a very strong piece of evidence in his favor. Could he simply have been unaware of the experiment at the time of writing the paper?

Einstein’s own recollections on this point were not entirely consistent. He sometimes said he couldn’t remember if he had been aware in 1905 of Michelson's experiments, but at other times he acknowledged that he had known of it from having read the works of Lorentz. Indeed, considering Einstein’s obvious familiarity with Lorentz’s works, and given all the attention that Lorentz paid to Michelson’s ether drift experiments over the years, it’s difficult to imagine that Einstein never absorbed any reference to those experiments. Assuming he was aware of Michelson's results prior to 1905, why did he chose not to cite them in support of his second principle? Of course, his paper includes no formal “references” at all (which in itself seems peculiar, especially to modern readers accustomed to extensive citations in scholarly works), but it does refer to some other experiments and theories by name, so an explicit reference to Michelson’s result would not have been out of place.

One possible explanation for Einstein’s reluctance to cite Michelson, both in 1905 and subsequently, is that he was sophisticated enough to know that his “theory” was technically just a re-interpretation of Lorentz’s theory - making identical predictions - so it could not be preferred on the basis of agreement with experiment. To Einstein the most important quality of his interpretation was not its consistency with experiment, but it’s inherent philosophical soundness. In other words, conflict with experiment was bad, but agreement with experiment by means of ad hoc assumptions was hardly any better. His critique of Lorentz’s theory (or what he knew of it at the time) was not so much that it was empirically "wrong" (which it wasn’t), but that the length contraction and time dilation effects had been inserted ad hoc to match the null results Michelson. (It’s debatable whether this critique was justified, in view of the discussion in Section 1.5.) Therefore, Einstein would naturally have been concerned to avoid giving the impression that his relativistic theory had been contrived specifically to conform with Michelson’s results. He may well have realized that any appeal to the Michelson-Morley experiment in order to justify his theory would diminish rather than enhance its persuasiveness.

This is not to suggest that Einstein was being disingenuous, because it’s clear that the principles of special relativity actually do emerge very naturally from just the first-order effects of magnetic induction (for example), and even from more basic considerations of the mathematical intelligibility of Galilean versus Lorentzian transformations (as stressed by Minkowski in his famous 1908 lecture). It seems clear that Einstein’s explanations for how he arrived at special relativity were sincere expressions of his beliefs about the origins of special relativity in his own mind. He was focused on the phenomenon of magnetic induction and the unphysical asymmetry of the pre-relativistic explanations. This was combined with a strong instinctive belief in the complete relativity of physics. He told Shankland in 1950 that the experimental results which had influenced him the most were stellar aberration and Fizeau's measurements on the speed of light in moving water. "They were enough," he said.

Return to Table of Contents