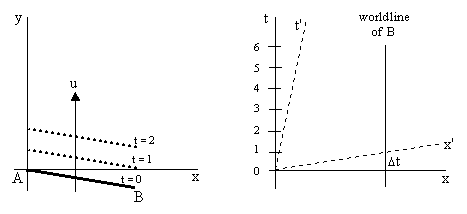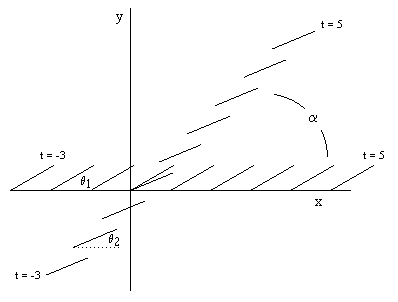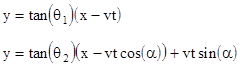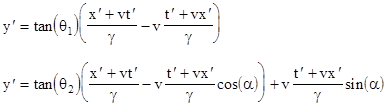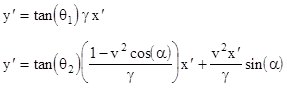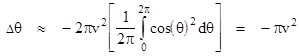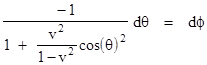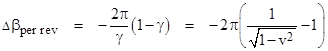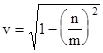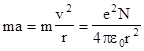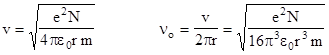|
2.11 Thomas Precession |
|
|
|
I feel it stealing now. Sentry, are you there? |
|
Just ease these darbies at the wrist, |
|
And roll me over fair! |
|
I am sleepy, and the oozy weeds about me twist. |
|
Herman Melville, 1891 |
|
|
|
Consider a slanted rod AB in the xy plane moving at speed u in the positive y direction as indicated in the left-hand figure below. The A end of the rod crosses the x axis at time t = 0, whereas the B end does not cross until time t = 1. Hence we conclude that the rod is oriented at some non-zero angle with respect to the xyt coordinate system. However, suppose we view the same situation with respect to a system of inertial coordinates x'y't' (with x' parallel to x) moving in the positive x direction with speed v. In accord with special relativity, the x' and t' axes are skewed with respect to the x and t axes as shown in the right-hand figure below. |
|
|
|
|
|
|
|
As a result of this skew, the B end of the rod crosses the x' axis at the same instant (i.e., the same t') as does the A end of the rod, which implies that the rod is parallel to the x' axis - and therefore to the x axis - based on the simultaneity of the x'y't' inertial frame. This implies that if a rod was parallel to the x axis and moving in the positive x direction with speed v, it would be perfectly aligned with the rod AB as the latter passed through the x' axis. Thus if a rod is initially aligned with the x axis and moving with speed v in the positive x direction relative to a given fixed inertial frame, and then at some instant with respect to the rod's inertial rest frame it instantaneously changes course and begins to move purely in the positive y direction, without ever changing its orientation, we find that its orientation does change with respect to the original fixed frame of reference. This is because the changes in the states of motion of the individual parts of the rod do not occur simultaneously with respect to the original rest frame. |
|
|
|
In general, whenever we transport a vector, always spatially parallel to itself in its own instantaneous rest frame, over an accelerated path, we find that its orientation changes relative to any given fixed inertial frame. This is the basic idea behind Thomas precession, named after Llewellyn Thomas, who first wrote about it in 1927. For a simple application of this phenomenon, consider a particle moving around a circular path. The particle undergoes continuous acceleration, but at each instant it is at rest with respect to the momentarily co-moving inertial frame. If we consider the "parallel transport" of a vector around the continuous cycle of momentary inertial rest frames of the particle, we find that the vector does not remain fixed. Instead, it "precesses" as we follow it around the cycle. This relativistic precession (which has no counter-part in non-relativistic physics) actually has observable consequences in the behavior of sub-atomic particles (see below). |
|
|
|
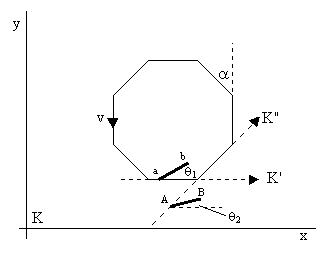
To understand how the Thomas precession for simple circular motion can be deduced from the basic principles of special relativity, we can begin by supposing the circular path of a particle is approximated by an n-sided polygon, and consider the transition from one of these sides to the next, as illustrated below. |
|
|
|
|
|
|
|
Let v denote the circumferential speed of the particle in the counter-clockwise direction, and note that α = 2π/n for an arbitrary n-sided regular polygon. (In the drawing above we have set n = 8). The dashed lines represent the loci of positions of the spatial origins of two inertial frames K' and K" that are co-moving with the particle on consecutive edges. |
|
|
|
Now suppose the vector ab at rest in K' makes an angle θ1 with respect to the x axis (in terms of frame K), and suppose the vector AB at rest in K" makes an angle of θ2 with respect to the x axis. The figure below shows the positions of these two vectors at several consecutive instants of the frame K. |
|
|
|
|
|
|
|
Clearly if θ1 is not equal to θ2, the two vectors will not coincide at the instant when their origins coincide. However, this assumes we use the definition of simultaneity associated with the inertial coordinate system K (i.e., the rest system of the polygon). The system K' is moving in the positive x direction at the speed v, so its time-slices are skewed relative to those of the polygon's frame of reference. Because of this skew, it is possible for the vectors ab and AB to be parallel with respect to K' even though they are not parallel with respect to K. |
|
|
|
The equations of the moving vectors ab and AB are easily seen to be |
|
|
|
|
|
|
|
This confirms that at t = 0 (or at any fixed t) these lines are not parallel unless θ1 = θ2. However, if we substitute from the Lorentz transformation between the frames K and K' |
|
|
|
|
|
|
|
where |
|
|
|
|
|
|
|
At t' = 0 these equations reduce to |
|
|
|
|
|
|
|
In the limit as the number n of sides of the polygon increases and the angle α approaches zero, the value of cos(α) approaches 1 (to the second order), and the value of sin(α) approaches α. Hence the equations of the two moving vectors approach |
|
|
|
|
|
|
|
Setting these equal to each other, multiplying through by γ/x', and re-arranging, we get the condition |
|
|
|
|
|
|
|
Recalling the trigonometric identity |
|
|
|
|
|
|
|
and noting that θ1 approaches θ2 in the limit as α goes to zero, the right-hand factor on the right side can be taken as |
|
|
|
|
|
|
|
where θ is the limiting value of both θ1 and θ2 as α goes to zero. Making use of these substitutions, and also noting that tan(θ2 θ1) approaches θ2 θ1, the condition for the two families of lines to be parallel with respect to frame K' (in the limit as α goes to zero) is |
|
|
|
|
|
|
|
This is the amount by which the two vectors are skewed with respect to the K frame due to the transition around a single vertex of the polygon, given that the transported vector makes an angle θ with the edge leading into the vertex. The total precession resulting from one complete revolution around the n-sided polygon is n times the mean value of θ2 θ1 for each of the n vertices of the polygon. Since n = 2π/α, we can express the total precession as |
|
|
|
|
|
|
|
If the circumferential speed v is small compared with 1, the denominator of this expression is closely approximated by 1, and the transported vector changes its absolute orientation only very slightly on one revolution. In this case it follows that θ varies essentially uniformly from 0 to 2π as the vector is transported around the circle. Hence for small v the total precession for one revolution is given closely by |
|
|
|
|
|
|
|
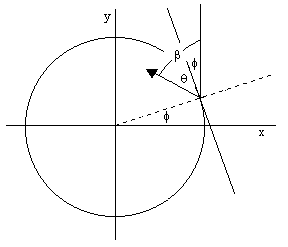
On the other hand, if v is not small, we can consider the general situation illustrated below: |
|
|
|
|
|
|
|
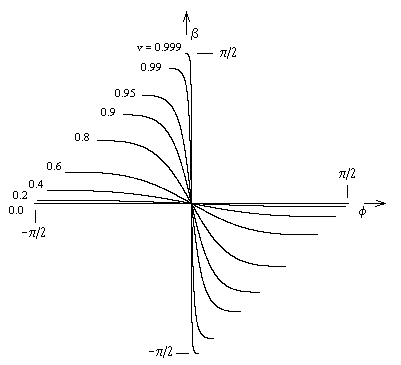
The variable ϕ signifies the absolute angular position of the transported vector at any given time, and β signifies the vector's orientation relative to the positive y axis. As before, θ denotes the angle of the vector relative to the local tangent "edge". We have the relations |
|
|
|
|
|
|
|
We also have the following identifications involving the parameters ϕ and β: |
|
|
|
|
|
|
|
Substituting dϕ + dθ for dβ and re-arranging, we get |
|
|
|
|
|
|
|
This can be integrated explicitly to give ϕ as a function of θ. Since β equals ϕ + θ, we can also give β as a function of θ, leading to the parametric equations |
|
|
|
|
|
|
|
where |
|
|
|
|
|
|
|
Consequently, a full cycle of ϕ corresponds to 2/γ times the above range, and so the average change in β per revolution (i.e., per 2π increase in ϕ) is |
|
|
|
|
|
|
|
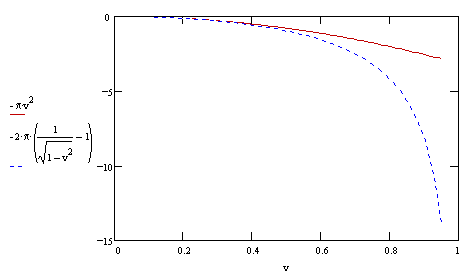
This function is plotted in the figure below, along with the "small v" approximation. |
|
|
|
|
|
|
|
For all v less than 1 we can expand the general expression into a series |
|
|
|
|
|
|
|
These expressions represent the average change per revolution, because the cycles of β do not in general coincide with the cycles of ϕ. Resonance occurs when the ratio of the change in ϕ to the change in β is rational. This is true if and only if there exist integers M,N such that |
|
|
|
|
|
|
|
Adding 1 to both sides, we can set 1 + (M/N) equal to m/n for integers m and n, and we can then square both sides and re-arrange to give, we find that the "resonant" values of v are given by |
|
|
|
|
|
|
|
where m,n are integers with |n| less than |m|. |
|
|
|
We previously derived the low-speed approximation of the amount Thomas precession for a vector subjected to "parallel transport" around a circle with a constant circumferential speed v in the form πv2 radians per revolution. Dividing this by 2π gives the average precession rate of v2/2 in units of radians per radian (of travel around the circle). We can also determine the average rate of Thomas precession, with units of radians per second. Letting ωo denote the orbital angular velocity (i.e., the angular velocity with which the vector is transported around the circle of radius r), we have v = ωor and a = v2/r where a is the centripetal acceleration. Hence we have ωo = v/r = a/v, so multiplying v2/2 by ωo gives the average Thomas precession rate ωT = va/2 in units of rad/sec, which represents a frequency of νT = (v2/2)νo = va/(4π) cycles/sec. |
|
|
|
Since the magnitude πv2 of the Thomas precession is of the second order in v, we might be tempted to think it is insignificant for ordinary terrestrial phenomena, but the expression νT = (v2/2)νo shows that the precession frequency can be quite large in absolute terms, even if v is small, provided νo is sufficiently large. This occurs when the orbital radius r is very small, giving a very large acceleration for any given orbital velocity. Consider, for example, the orbit of an electron around the nucleus of an atom. An electron has intrinsic quantum "spin" which tends to maintain it's absolute orientation much as does a spinning gyroscope, so it can be regarded as a vector undergoing parallel transport. Now, according to the original (naive) Bohr model, the classical orbit of an electron around the nucleus is given by equating the Coulomb and centripetal forces |
|
|
|
|
|
|
|
where e is the charge of an electron, m is the mass, ε0 is the permittivity of the vacuum, and N is the atomic number of the nucleus, so the linear and angular speeds of the electron are |
|
|
|
|
|
|
|
Bohr hypothesized that the angular momentum L = mvr can only be an integer multiple of h/(2π), so we have for some positive integer n |
|
|
|
|
|
|
|
Therefore, the linear velocity and orbital frequency of an electron (in this simplistic model) are |
|
|
|
|
|
|
|
where α = e2/(2hε0) is the dimensionless "fine structure constant", whose value is approximately 1/137. (Remember that we are using units such that c = 1, so all distances are expressed in units of seconds.) For the lowest energy state of a hydrogen atom we have n = N = 1, so the linear speed of the electron is about 1/137. Consequently the precession frequency is (v2/2) = 0.00002664 times the orbital frequency, which is a very small fraction, but it is still a very large frequency in absolute terms (1.755E-11 cycles/sec) because the orbital frequency is so large. (Note that these are not the frequencies of photons emitted from the atom, because those correspond to quanta of light given off due to transitions from one energy level to another, whereas these are the theoretical orbital frequencies of the electron itself in Bohr's simple model.) |
|
|
|
Incidentally, there is a magnetic interaction between the electron and nucleus of some atoms that is predicted to cause the electron's spin axis to precess by +v2 radians per orbital radian, but the actual observed precession rate of the spin axes of electrons in such atoms is only +(v2/2). For awhile after its discovery, there was no known explanation for this discrepancy. Only in 1927 did Thomas point out that special relativity implies the purely kinematic relativistic effect that now bears his name, which (as we've seen) yields a precession of (v2/2) radians per orbital radian. The sum of this purely kinematic effect due to special relativity with the predicted effect due to the magnetic interaction yields the total observed +(v2/2) precession rate. |
|
|
|
It's often said that the relativistic effect supplies a "factor of 2" (i.e., divides by 2) to the electron's precession rate. For example, Uhlenbeck wrote that |
|
|
|
...when I first heard about [the Thomas precession], it seemed unbelievable that a relativistic effect could give a factor of 2 instead of something of order v/c... Even the cognoscenti of relativity theory (Einstein included!) were quite surprised. |
|
|
|
(Uhlenbeck also told Pais that he didn't understand a word of Thomas's work when it first came out.) However, this description is somewhat misleading, because (as we've seen) the relativistic effect is actually additive, not multiplicative. It just so happens that a particular magnetic interaction yields a precession of twice the frequency, and the opposite sign, as the Thomas precession, so the sum of the two effects is half the size of the magnetic effect alone. Both of the effects are second-order in the linear speed v/c. |
|
|