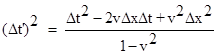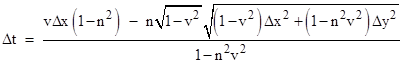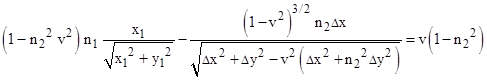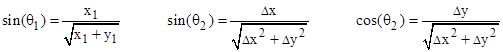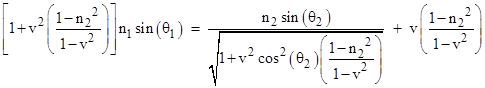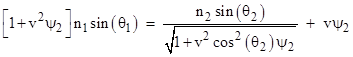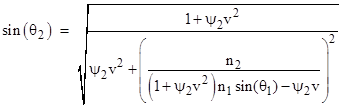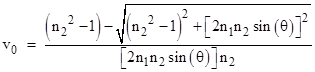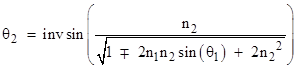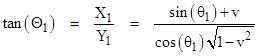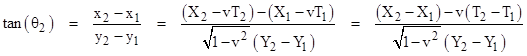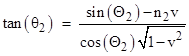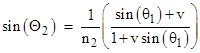Refraction At A Plane Boundary Between Moving Media

Mathematicians usually consider the Rays of Light to be Lines reaching from the luminous Body to the Body illuminated, and the refraction of those Rays to be the bending or breaking of those lines in their passing out of one Medium into another. And thus may Rays and Refractions be considered, if Light be propagated in an instant. But by an Argument taken from the Equations of the times of the Eclipses of Jupiter's Satellites, it seems that Light is propagated in time, spending in its passage from the Sun to us about seven Minutes of time: And therefore I have chosen to define Rays and Refractions in such general terms as may agree to Light in both cases.

                                                        Isaac Newton (Opticks), 1704

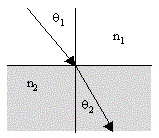
The ray angles θ₁ and θ₂ for incident and refracted optical rays at a plane boundary between regions of constant indices of refraction n₁ and n₂ are related according to Snell’s law

However, this formula applies only if the media (which are assumed to have isotropic indices of refraction with respect to their rest frames) are at rest relative to each other. If the media are in relative transverse motion, it is necessary to account for the effect of aberration on the ray angles relative to the rest frames of the respective media. The result is that the effective refraction is a function of the relative transverse velocity of the media. Thus, measurements of the optical refraction could (in principle) be used to determine the velocity of a moving volume of fluid. Unlike Doppler shift measurement techniques, this approach does not rely on the presence of discrete particles in the fluid, and involves only measurements of direct, rather than reflected, light signals.

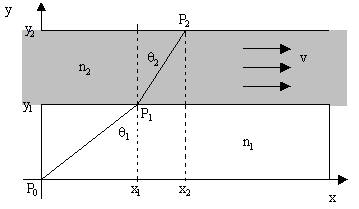
Since the amount of refraction at a boundary depends on the angle of incidence with respect to the rest frames of the media, it follows that if the media have different rest frames the simple form of Snell’s law does not apply directly, because it will be necessary to account for aberration. To derive the law of refraction for transversely moving media, consider the arrangement shown in the figure below, drawn with respect to a system of coordinates (x,y,t) relative to which the medium with refractive index n₁ is at rest.

In these coordinates the medium with index n₂ is moving transversely with a speed v. By both Fermat’s principle of “least time” and the principles of quantum electrodynamics, we know that the path of light from point P₀ to point P₂ is such that the travel time is stationary (which, in this case, means minimized), so if we express the total travel time as a function of the x coordinate of the “corner point” P₁, we can differentiate to find the position that minimizes the time, and from this we can infer the angles of incidence and refraction.

With respect to the xyt coordinates in which the n₁ medium is at rest, the squared spatial distance from P₀ to P₁ is x₁² + y₁², so the time required for light to traverse that distance is

On the other hand, for the trip from point P₁ to point P₂ we need to know the distance traveled with respect to the coordinates x'y't' in which the n₂ medium is at rest. If we define

then the Lorentz transformation gives us the corresponding increments in the primed coordinates

Therefore, the squared spatial and temporal distances from P₁ to P₂ in the n₂ rest coordinates are given by

Since the ratio of these increments equals the square of the speed of light in the n₂ medium, which is 1/n₂², we have

Solving this quadratic for Δt, which equals t_C – t_B, gives

Differentiating with respect to Δx, and noting that d(Δx)/dx₁ = –1, we can minimize the total travel time t₂ – t₀ by adding the derivatives of Δt and t₁ – t₀ with respect to x₁, and setting the result to zero. This leads to the condition

Making the substitutions

we arrive at the equation for refraction at the plane boundary between transversely moving media

As expected, this reduces to Snell’s law for stationary media if we set v = 0. Also, if the moving medium has a refractive index of n₂ = 1, this equation again reduces to Snell’s law, regardless of the velocity, because the concept of speed doesn’t apply to the vacuum. If we define the parameter

then the refraction equation can be written more compactly as

This can be solved explicitly for sin(θ₂) to give the result

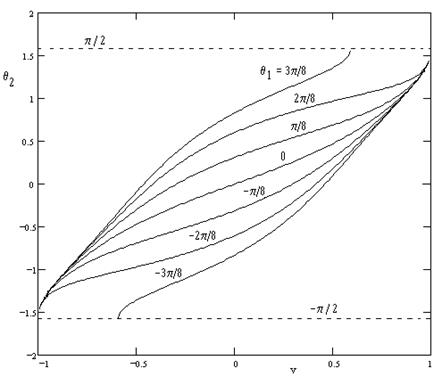
with the appropriate sign for the square root. Taking n₁ = 1.2 and n₂ = 1.5, the figure below shows the angle of refraction θ₂ as a function of the transverse speed v of the medium with various angles of incidence θ₁ ranging from –3π/8 to +3π/8 radians.

Incidentally, when plotting these lines it is necessary to take the positive root when v is above the zero-crossing speed, and the negative root when v is below. The zero-crossing speed (i.e., the speed v when the refracted angle is zero) is

The figure shows that at high relative speeds and high angle of incidence we can achieve total internal reflection, even though the downstream medium is more dense than the upstream medium. The critical conditions occur when the squared quantity in parentheses in the equation for sin(θ₂) reaches ±1, which implies

Solving these two quadratics for v (remembering that ψ₂ is a function of v), we have the four distinguished speeds

The two speeds given by ±1/n₂ (which are just the speeds of light in the moving medium) generally correspond to removable singularities, because both the numerator and denominator of the expression for sin(θ₂) vanish. At these speeds the values of θ₂ can be assigned continuously as

It isn’t clear what, if any, optical effects would appear at these two removable singularities. The other two distinguished speeds represent the onset of total internal reflection if their values fall in the range from –1 to +1. For example, the figure above shows that total internal reflection for an incident angle of θ₁ = 3π/8 with n₁ = 1.2 and n₂ = 1.5 begins when the speed v exceeds

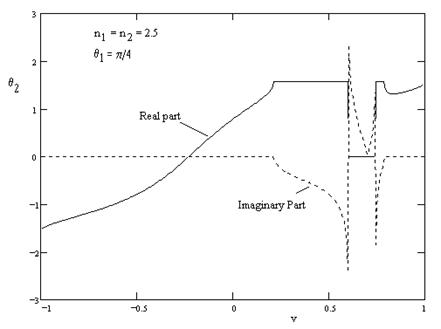
Notice that for an incidence angle of zero, this speed is simply n₂, which is ordinarily greater than 1, and thus outside the range of achievable speeds (since we assume the medium itself is moving through a vacuum). However, for non-zero angles of incidence it is possible for one of these two critical speeds to lie in the achievable range. In fact, for certain values of n₁, n₂, and θ₁, it is possible for all four of the critical speeds to lie within the achievable range, leading to some interesting phenomena. For example, with n₁ = n₂ = 2.5 and with θ₁ = 45 degrees, the refracted angle as a function of medium speed is as shown below.

In this case the distinguished speeds are –0.4, +0.203, +0.4, and +0.783. This suggests that as the transverse speed of the medium increases from 0, the refracted ray becomes steeper until reaching 90 degrees at v = +0.203, at which point there is total internal reflection. This remains the case until achieving a speed of +0.783, at which point some refraction is re-introduced, and the refracted angle sweeps back from +90 to about +80 degrees (relative to the stationary frame), and then back to +90 degrees as speed continues to increase to 1. This can be explained in terms of the variations in the effective critical angle and the aberration angle. As speed increases, the effective critical angle for total internal reflection initially increases faster than the aberration angle, pushing the ray into total internal reflection. However, eventually (at close to the speed of light) the aberration effect brings the incident ray back into the refractive range.

For an alternative derivation that leads to a different, but equivalent, relation, suppose the index of refraction of the stationary region is n₁ = 1, which implies this region is a vacuum. If we let d₁ denote the spatial distance from P₀ to P₁ with respect to the rest frame, then we have

These are the components of the interval P₀ to P₁ with respect to the rest frame of n₁, and they can be converted to the frame of n₂ (denoted by upper case letters) using the Lorentz transformation

For convenience we have reversed the sense of v from the previous discussion. Letting Θ₁ denote the angle θ₁ with respect to the moving n₂ coordinate system, we can express the tangent of this angle as

Taking the sine of the inverse tangent of both sides gives the familiar aberration formula

Since we are assuming the n₁ medium is a vacuum, we are free to treat the entire configuration as being at rest in the n₂ coordinates, with the angle of incidence as defined above. Therefore, Snell’s law for stationary media can be applied to give the refracted angle relative to these coordinates

Now, if D₂ is the spatial distance from P₁ to P₂ with respect to the moving coordinates, we have

Also, the Lorentz transformation gives the coordinates of points P₁ and P₂ in the rest frame in terms of the coordinates in the moving frame as follows:

From these we can construct the tangent of θ₂ with respect to the rest coordinates

Substituting for the coordinate differences gives

We saw previously that

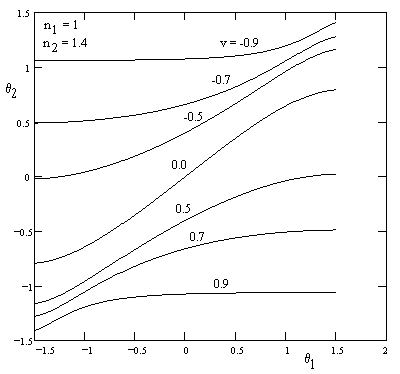
so we can explicitly compute θ₂ from θ₁. It can be shown that this solution is identical to the solution (with n₁ = 1) derived previously on the basis of Fermat's principle (noting that we here defined v as the speed of the n₁ medium relative to the n₂ medium, so the sign of v is reversed from the previous formula). Furthermore, we can solve these equations for sin(θ₁) as a function of θ₂ and then by equating this sin(θ₁) with n₃ sin(θ₃) for a stationary medium neighboring the vacuum region, we again have the general solution for two refractive media in relative transverse motion. A plot of θ₂ from θ₁ for various values of v is shown below:

Return to Table of Contents