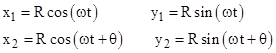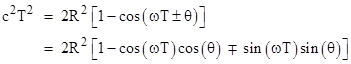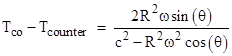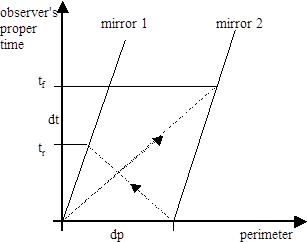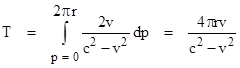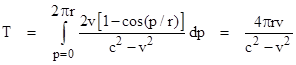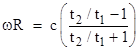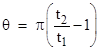The Sagnac Effect

Blind unbelief is sure to err,

And scan his work in vain;

God is his own interpreter,

And he will make it plain.

              William Cowper, 1780

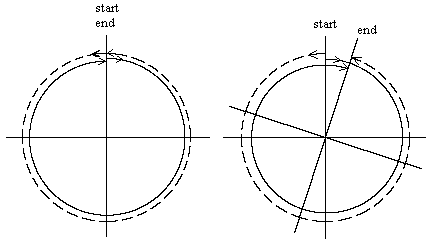
If two pulses of light are sent in opposite directions around a stationary circular loop of radius R, they will travel (in terms of any inertial coordinate system, such as that in which the center is at rest) the same distance at the same speed, so they arrive at the end point simultaneously. This is illustrated in the left-hand figure below.

The figure on the right indicates what happens if the loop itself is rotating during this procedure. Clearly the pulse traveling in the same direction as the rotation of the loop must travel a slightly greater distance than the pulse traveling in the opposite direction, due to the angular displacement of the loop during the transit. As a result, if the pulses are emitted simultaneously from the “start” position, the counter-rotating pulse will arrive at the "end" point slightly earlier than the co-rotating pulse. Conversely, if two pulses arrive simultaneously at the end point, the co-rotating pulse must have been emitted from the starting point earlier than the counter-rotating pulse.

Quantitatively, if we let ω denote the angular speed of the loop, then the circumferential tangent speed of the end point is v = ωR, and the sum of the speeds of the pulses and the receiver at the "end" point is c–v in the co-rotating direction and c+v in the counter-rotating direction. Both pulses begin with an initial separation of 2πR from the end point, so the difference between the travel times is

where A = πR² is the area enclosed by the loop. The corresponding phase difference for light of frequency ν radians/second (in the rest frame of the center of rotation) is simply Δϕ = νΔt, and since ν = 2πc/λ, the phase difference can be written as (8πAcω/λ)/(c² – v²).

This analysis is perfectly valid in both the classical and the relativistic contexts. Of course, the result represents the time difference with respect to the axis-centered inertial frame. A clock attached to the perimeter of the ring would, according to special relativity, record a lesser time, by the factor γ = (1–(v/c)²)^1/2, so the Sagnac delay with respect to such a clock would be [4Aω/c²]/(1–(v/c)²)^1/2. However, the characteristic frequency of a given light source co-moving with this clock would be greater, compared to its reduced value in terms of the axis-centered frame, by precisely the same factor, so the actual phase difference of the beams arriving at the receiver is invariant. (It's also worth noting that there is no Doppler shift involved in a Sagnac device, because each successive wave crest in a given direction travels the same distance from transmitter to receiver, and clocks at those points show the same lapse of proper time, both classically and in the context of special relativity.)

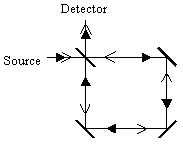
This phenomenon applies to any closed loop, not necessarily circular. For example, suppose a beam of light is split by a half-silvered mirror into two beams, and those beams are directed in a square path around a set of mirrors in opposite directions as shown below.

Just as in the case of the circular loop, if the apparatus is unaccelerated, the two beams will travel equal distances around the loop, and arrive at the detector simultaneously and in phase. However, if the entire device (including source and detector) is rotating, the beam traveling around the loop in the direction of rotation will have farther to go than the beam traveling counter to the direction of rotation, because during the period of travel the mirrors and detector will all move (slightly) toward the counter-rotating beam and away from the co-rotating beam. Consequently the beams will reach the detector at slightly different times, and slightly out of phase, producing optical interference "fringes" that can be observed and measured.

Michelson had proposed constructing such a device in 1904, but did not pursue it at the time, since he realized it would show only the absolute rotation of the device. The effect was first demonstrated in 1911 by Harress (unwittingly) and in 1913 by Georges Sagnac, who published two brief notes in the Comptes Rendus describing his apparatus and summarizing the results. He wrote

The result of measurements shows that, in ambient space, the light is propagated with a speed V₀, independent of the overall movement of the source of light O and optical system.

This rules out any conceptually coherent ballistic theory of light propagation, according to which the speed of light is the vector sum of the velocity of the emitting particle plus a vector of magnitude c. Ironically, the original Michelson-Morley experiment was consistent with the ballistic theory, but inconsistent with the naïve ether theory, whereas the Sagnac effect is consistent with the naïve ether theory but inconsistent with the ballistic theory. Both results are consistent with fully relativistic theories of Lorentz and Einstein, since according to both theories light is propagated at a speed independent of the state of motion of the source.

Because of the incredible precision of interferometric techniques, devices like this are capable of detecting and measuring extremely small amounts of absolute rotation. One of the first applications of this phenomenon was an experiment performed by Michelson and Gale in 1925 to measure the absolute rotation rate of the Earth by means of a rectangular optical loop 2/5 mile long and 1/5 mile wide. (See below for Michelson’s comments on this experiment.) More recently, the invention of lasers around 1963 has led to practical small-scale devices for measuring rotation by exploiting the Sagnac effect. There are two classes of such devices, namely, ring interferometers and ring lasers. A ring interferometer typically consists of many windings of fiber optic lines, conducting light (of a fixed frequency) in opposite directions around a loop, and then recombining them to measure the phase difference, just as in the original Sagnac apparatus, but with greater efficiency and sensitivity. A ring laser, on the other hand, consists of a laser cavity in the shape of a ring, which allows light to circulate in both directions, producing two standing waves with the same number of nodes in each direction. Since the optical path lengths in the two directions are different, the resonant frequencies of the two standing waves are also different. (In practice it is typically necessary to “dither” the ring to prevent phase locking of the two modes.) The “beat” between the two frequencies is measured, giving a result proportional to the rotation rate of the device. Incidentally, it isn’t necessary for the actual laser cavity to circumscribe the entire loop; longitudinal pumping can be used, driven by feedback carried in opposite directions around the loop in ordinary optical fibers. (Needless to say, the difference in resonant frequency of the two standing waves in a ring laser due to the different optical path lengths is not to be confused with a Doppler shift.) Today such devices are routinely used in guidance and navigation systems for commercial airliners, nautical ships, spacecraft, and in many other applications, and are capable of detecting rotation rates as slight as 0.00001 degree per hour.

We saw previously that the time delay (and therefore the difference in the optical path lengths) for a circular loop is proportional to the area enclosed by the loop. This interesting fact actually applies to arbitrary closed loops. To prove this, we will derive the difference in arrival times of the two pulses of light for an arbitrary polygonal loop inscribed in a circle. Let the (inertial) coordinates of two consecutive mirrors separated by a subtended angle θ be

where ω is the angular velocity of the device. Since light rays travel along null intervals, we have c²(dt)² = (dx)² + (dy)², so the coordinate time T required for a light pulse to travel from one mirror to the next in the forward and reverse directions satisfies the equations

Typically ωT is extremely small, i.e., the polygon doesn't rotate through a very large angle in the time it takes light to go from one mirror to the next, so we can expand these equations in ωT (up to second order) and collect powers of T to give the quadratic

The two roots of this polynomial are the values of T, one positive and one negative, for the co-rotating and counter-rotating solutions, so the difference in the absolute times is the sum of these roots. Hence we have

This is the net contribution of this edge to the total time increment. Recalling that the area of a regular n-sided polygon of radius R is nR²sin(2π/n)/2, the area of the triangle formed by the hub and the two mirrors is R²sin(θ)/2. It follows that each edge of an arbitrary polygonal loop inscribed in a circle contributes 4A_iω/(c² – v²cos(θ)) to the total time discrepancy, where A_i is the area of the ith triangular slice of the loop and v = Rω is the tangential speed of the mirrors. Therefore, the total discrepancy in travel times for the co-rotating and counter-rotating beams around the entire loop is simply

where A is the total area enclosed in the loop. This applies to polygons with any number of sides, including the limiting case of circular fiber-optic loops with virtually infinitely many edges (where the "mirrors" are simply the inner reflective lining of the fiber-optic cable), in which case θ goes to zero and the denominator of the phase difference is simply c² – v². For realistic values of v (i.e., very small compared with c), the phase difference reduces to the well-known result 4Aω/c². It's worth noting that nothing in this derivation is unique to special relativity, because the Sagnac effect is a purely "classical" effect. The apparatus is set up as a differential device, so the relativistic effects apply equally in both directions, and hence the higher-order corrections of special relativity cancel out of the phase difference.

Despite the ease and clarity with which special relativity accounts for the Sagnac effect, one occasionally sees claims that this effect entails a conflict with the principles of special relativity. The usual claim is that the Sagnac effect somehow falsifies the invariance of light speed with respect to all inertial coordinate systems. Of course, it does no such thing, as is obvious from the fact that the simple description of an arbitrary Sagnac device given above is based on isotropic light speed with respect to one particular system of inertial coordinates, and all other inertial coordinate systems are related to this one by Lorentz transformations, which are defined as the transformations that preserve light speed. Hence no description of a Sagnac device in terms of any system of inertial coordinates can possibly entail non-isotropic light speed, nor can any such description yield physically observable results different from those derived above, which are known to agree with experiment. (We need hardly add that relativity, based on the principle of inertia, is not to be conflated with naive relationism.)

Nevertheless, it remains a seminal tenet of anti-relativityism (for lack of a better term) that the trivial Sagnac effect somehow "disproves relativity". Those who espouse this view sometimes claim that the expressions "c+v" and "c–v" appearing in the derivation of the phase shift are prima facie proof that the speed of light is not c with respect to some inertial coordinate system. When it is pointed out that those quantities do not refer to the speed of light, but rather to the sum and difference of the speed of light and the speed of some other object, both with respect to a single inertial coordinate system, which can be as great as 2c according to special relativity, the anti-relativityists are undaunted, and merely proceed to construct progressively more convoluted and specious "objections". For example, they sometimes argue that each point on the perimeter of a rotating circular Sagnac device is always instantaneously at rest in some inertial coordinate system, and according to special relativity the speed of light is precisely c in all directions with respect to any inertial system of coordinates, so (they argue) the speed of light must be isotropic at every point around the entire circumference of the loop, and hence the light pulses must take an equal amount of time to traverse the loop in either direction. Needless to say, this "reasoning" is invalid, because the pulses of light are never (let alone always) at the same point in the loop at the same time during their respective trips around the loop in opposite directions. At any given instant the point of the loop where one pulse is located is necessarily accelerating with respect to the instantaneous inertial rest frame of the point on the loop where the other pulse is located (and vice versa). As noted above, it’s self-evident that since the speed of light is isotropic with respect to at least one particular frame of reference, and since every other frame is related to that frame by a transformation that explicitly preserves light speed, no inconsistency with the invariance of the speed of light can arise.

Having accepted that the observable effects predicted by special relativity for a Sagnac device are correct and entail no logical inconsistency, the dedicated opponents of special relativity sometimes resort to claims that there is nevertheless an inconsistency in the relativistic interpretation of what's really happening locally around the device in certain extreme circumstances. The fundamental fallacy underlying such claims is the idea that the beams of light are traveling the same, or at least congruent, inertial paths through space and time as they proceed from the source to the detector. If this were true, their inertial speeds would indeed need to differ in order for their arrival times at the detector to differ. However, the two pulses do not traverse congruent paths from emission to detector (assuming the device is absolutely rotating). The co-rotating beam is traveling slightly farther than the counter-rotating beam in the inertial sense, because the detector is moving away from the former and toward the latter while they are in transit. Naturally the ratio of optical path lengths is the same with respect to any fixed system of inertial coordinates.

It’s also obvious that the absolute difference in optical path lengths cannot be "transformed away", e.g., by analyzing the process with respect to coordinates rigidly attached to and rotating along with the device. We can, of course, define a system of coordinates in terms of which the position of a point fixed on the disk is independent of the time coordinate, but such coordinates are necessarily rotating (accelerating), and special relativity does not entail invariant or isotropic light speed with respect to non-inertial coordinates. (In fact, one need only consider the distant stars circumnavigating the entire galaxy every 24 hours with respect to the Earth's rotating system of reference to realize that the limiting speed of travel is generally not invariant and isotropic in terms of accelerating coordinates.) A detailed analysis of a Sagnac device in terms of non-inertial (i.e., rotating) coordinates is presented in Section 4.8, and discussed from a different point of view in Section 5.1. For the present, we confine our attention to inertial coordinates, and demonstrate how a Sagnac device is described in terms of instantaneously co-moving inertial frames of an arbitrary point on the perimeter.

Suppose we've sent a sequence of momentary pulses around the loop, at one-second intervals, in both directions, and we have photo-detectors on each mirror to detect when they are struck by a co-rotating or counter-rotating pulse. Clearly the pulses will strike each mirror at one-second intervals from both directions (though not necessarily synchronized) because if they were arriving more frequently from one direction than from the other, the secular lag between corresponding pulses would be constantly increasing, which we know is not the case. So each mirror is receiving one pulse per second from both directions. Furthermore, a local measurement of light speed performed (over a sufficiently short period of time) by an observer riding along at a point on the perimeter will necessarily show the speed of light to be c in all direction with respect to his instantaneously co-moving inertial coordinates. However, this system of coordinates is co-moving with only one particular point on the rim. At other points on the rim these coordinates are not co-moving, and so the speed of light is not c at other points on the rim with respect to these coordinates.

To describe this in detail, let's first analyze the Sagnac device from the hub-centered inertial frame. Throughout this discussion we assume an n-sided polygonal loop where n is very large, so the segment between any two adjacent mirrors subtends only a very small angle. With respect to the hub-centered frame each segment is moving with a velocity v parallel to the direction of travel of the light beams, so the situation on each segment is as plotted below in terms of hub-frame coordinates:

In this drawing, t_f is the time required for light to cross this segment in the co-rotating direction, and t_r is the time required for light to cross in the counter-rotating direction. The difference between these two times, denoted by dt, is the incremental Sagnac effect for a segment of length dp on the perimeter.

Now, the ratio of dt/dp as a function of the rim velocity v can easily be read off this diagram, and we find that

This can be taken as a measure of the anisotropy over an incremental segment with respect to the hub frame. (Notice that this anisotropy with respect to the conventional relativistic spacetime decomposition for any inertial frame is actually in the distance traveled, not the speed of travel.) All the segments are symmetrical in this frame, so they all have this same anisotropy. Therefore, we can determine the total difference in travel times for co-rotating and counter-rotating beams of light making a complete trip around the loop by integrating dt around the perimeter. Thus we have

Substituting ωr in place of v in the numerator, and noting that the enclosed area is A = πr², we again arrive at the result T = 4Aω/(c² – v²).

Now let's analyze the loop with respect to one of our tangential frames of reference, i.e., an inertial frame that is momentarily co-moving with one of the segments on the rim. If we examine the situation on that particular segment in terms of its own co-moving inertial frame we find, not surprisingly, the situation shown below:

This shows that dt/dp = 0, meaning no anisotropy at all. Nevertheless, if the light beams are allowed to go all the way around the loop, their total travel times will differ by T as computed above, so how does that difference arise with respect to this tangential frame?

Notice that although dt/dp equals zero at this tangent point with respect to the tangent frame, segments 90 degrees away from this point have the same anisotropy as we found for all the segments relative to the hub frame, namely, dt/dp = 2v/(c² – v²), because the velocity of those two segments relative to our tangential frame is exactly v along the direction of the light rays, just as it was with respect to the hub frame. Furthermore, the segment 180 degrees away from our tangent segment has twice the anisotropy as it has with respect to the original hub-frame inertial coordinates, because that segment has a velocity of 2v with respect to our tangential frame.

In general, the anisotropy dt/dp can be computed for any segment on the loop simply by determining the projection of that segment's velocity (with respect to our tangential frame) onto the axis of the light rays. This gives the results illustrated below, showing the ratio of the tangential frame anisotropy to the hub frame anisotropy:

It's easy to show that

where θ is the angle relative to the tangent point. To assess the total difference in arrival times for light rays going around the loop in opposite directions, we need to integrate dt by dp around the perimeter. Noting that θ equals p/r, we have

which again equals 4Aω/(c² – v²), in agreement with the hub frame analysis. Thus, although the anisotropy is zero at each point on the rim's surface when evaluated with respect to that point's co-moving inertial frame, we always arrive at the same overall non-zero anisotropy for the entire loop. This was to be expected, because the absolute physical situation and intervals are the same for all inertial frames. We're simply decomposing those absolute intervals into space and time components in different ways.

The union of all the "present" time slices of the sequence of instantaneous co-moving inertial coordinate systems for a point fixed on the rim of a rotating disk, with each time slice assigned a time coordinate equal to the proper time of the fixed point, constitutes a coherent and unambiguous coordinate system over a region of spacetime that includes the entire perimeter of the disk. The general relation for mapping the proper time of one worldline into another by means of the co-moving planes of simultaneity of the former is derived at the end of Section 2.9, where it is shown that the derivative of the mapped time from a point fixed on the rim to a point at the same radius fixed in the hub frame is positive provided the rim speed is less than c. Of course, for locations further from the center of rotation the planes of simultaneity of a revolving point fixed on the rim will be become "retrograde", i.e., will backtrack, making the coordinate system ambiguous. This occurs for locations at a distance greater than c²/a from the hub, where a is the acceleration of the point fixed on the rim.

It's also worth noting that the amount of angular travel of the device during the time it takes for one pair of light pulses to circumnavigate a circular loop is directly proportional to the net "anisotropy" in the travel times. To prove this, note that in a circular Sagnac device of radius R the beam of light in the direction of rotation travels a distance of (2π – ωt₁)R and the other beam goes a distance of (2π + ωt₂)R where t₁ and t₂ are the travel times of the two beams, and ω is the angular velocity of the loop. The travel times of the beams are just these distances divided by c, so we have

Solving for the times gives

so the difference in times is

where A = 2πR² and v = ωR. The "anisotropic ratio" is the ratio of the travel times, which is

Solving this for ωR gives

Letting θ denote the angular travel of the loop during the travel of the two light beams, we have

Substituting for ωR this reduces to

Therefore, the amount by which the ratio of travel times differs from 1 is exactly proportional to the angle through which the loop rotates during the transit of light, and this is true independent of R. (Increasing the radius has the effect of increasing the difference between the travel times, but it doesn't alter the ratio.)

It's worth emphasizing that the Sagnac effect is not strictly a relativistic phenomenon, because it's a "differential device", i.e., by running the light rays around the loop in opposite directions and measuring the time difference, it effectively cancels out the "transverse" effects that characterize relativistic phenomena. For example, the length of each incremental segment around the perimeter is shorter by a factor of [1–(v/c)²]^1/2 in the hub based frame than in it's co-moving tangential frame, but this factor applies in both directions around the loop, so it doesn't affect the differential time. Likewise a clock on the perimeter moving at the speed v runs slow, in accord with special relativity, but the frequency of the light source is correspondingly slow, and this applies equally in both directions, so this does not affect the phase difference at the receiver. Thus, a pure Sagnac apparatus does not discriminate between relativistic and pre-relativistic theories (although it does rule out any conceptually coherent ballistic theory). Ironically, this is the main reason it comes up so often in discussions of relativity, because the effect can easily be computed on a non-relativistic basis and treating light as a wave propagating in a stationary medium (with index of refraction equal to 1) at a fixed speed. Of course, if the light traveling around the loop passes through moving media with indices of refraction differing significantly from unity, then the Fizeau effect must also be taken into account, and in this case the results, while again perfectly consistent with special relativity, are quite problematic for any non-relativistic ether-based interpretation.

As mentioned above, as early as 1904 Michelson had proposed using such a device to measure the rotation of the earth, but he hadn't pursued the idea, since measurements of absolute rotation are fairly commonplace (e.g. Focault’s pendulum). Nevertheless, he (along with Gale) agreed to perform the experiment in 1925 (at considerable cost) at the urging of "relativists", who wished him to verify the shift of 236/1000 of a fringe predicted by special relativity. This was intended mainly to refute the theory of an ether fully dragged around with the spinning earth, along with the only physically plausible ballistic theory of light propagation, both of which predict zero phase shift (for a circular device). Michelson was not enthusiastic, since classical optics on the assumption of a stationary ether predicted exactly the same shift as does special relativity (as explained above). He said

We will undertake this, although my conviction is strong that we shall prove only that the earth rotates on its axis, a conclusion which I think we may be said to be sure of already.

As Harvey Lemon wrote in his biographical sketch of Michelson, "The experiment, performed on the prairies west of Chicago, showed a displacement of 230/1000, in very close agreement with the prediction. The rotation of the Earth received another independent proof, the theory of relativity another verification. But neither fact had much significance." Michelson himself wrote that "this result may be considered as an additional evidence in favor of relativity − or equally as evidence of a stationary ether".

The only significance of the Sagnac effect for special relativity (aside from providing another argument against the ballistic theory) is that although the effect itself is of the first order in v/c, the description of the local conditions on the disk in terms of inertial coordinates depends on second-order effects. These effects have been confirmed empirically by, for example, the Michelson-Morley experiment. Considering the Earth as a particle on a large Sagnac device as it orbits around the Sun, the ether drift experiments demonstrate these second-order effects, confirming that the speed of light is indeed invariant with respect to relatively moving systems of inertial coordinates.

Return to Table of Contents