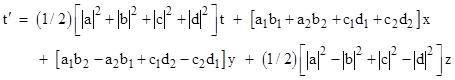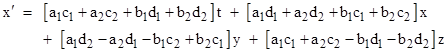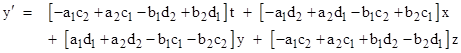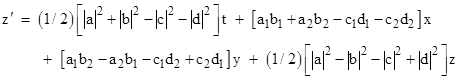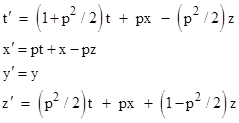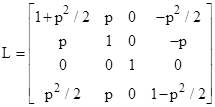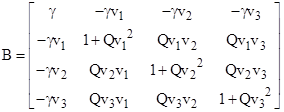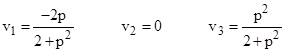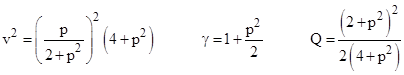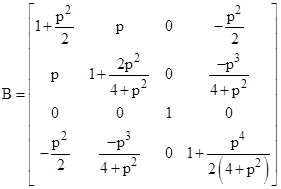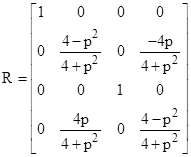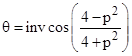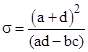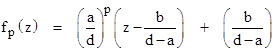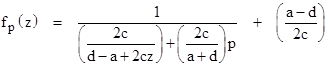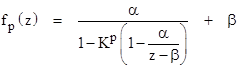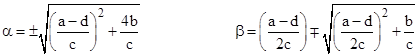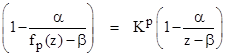2.6  Mobius Transformations of The Night Sky

So take this night,

Wrap it around me like a sheet.

I know I'm not forgiven

But I need a place to sleep...

                       Black Lab

Any proper orthochronous Lorentz transformation (including ordinary rotations and relativistic boosts) can be represented by

where

and Q* is the transposed conjugate of Q. The coefficients a,b,c,d of Q are allowed to be complex numbers, normalized so that ad – bc = 1. To be explicit, this implies that if we define

then the Lorentz transformation (1) is

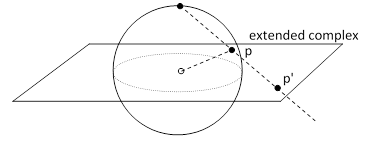
Two observers at the same point in spacetime but with different orientations and velocities will "see" incoming light rays arriving from different relative directions with respect to their own frames of reference, due partly to ordinary rotation, and partly to the aberration effect described in the previous section. This leads to the remarkable fact that the combined effect of any proper orthochronous (and homogeneous) Lorentz transformation on the incidence angles of light rays at a point corresponds precisely to the effect of a particular linear fractional transformation on the Riemann sphere via ordinary stereographic projection from the extended complex plane. The latter is illustrated below:

Roger Penrose described this as “the first step of a powerful correspondence between the spacetime geometry of relativity and the holomorphic geometry of complex spaces”. The complex number p in the extended complex plane is identified with the point p' on the unit sphere that is struck by a line from the "North Pole" through p. In this way we can identify each complex number uniquely with a point on the sphere, and vice versa. (The North Pole is identified with the "point at infinity" of the extended complex plane, for completeness.)

Relative to an observer located at the center of the Riemann sphere, each point of the sphere lies in a certain direction, and these directions can be identified with the directions of incoming light rays at a point in spacetime. If we apply a Lorentz transformation of the form (1) to this observer, specified by the four complex coefficients a,b,c,d, the resulting change in the directions of the incoming rays of light is given exactly by applying the linear fractional transformation (also known as a Mobius transformation)

to the points of the extended complex plane. Of course, our normalization ad – bc = 1 implies the two conditions

so of the eight coefficients needed to specify the four complex numbers a,b,c,d, these two constraints reduce the degrees of freedom to six, which is precisely the number of degrees of freedom of Lorentz transformations (namely, three velocity components v_x,v_y,v_z, and three angular specifications for the longitude and latitude of our line of sight and orientation about that line).

To illustrate this correspondence, first consider the "identity" Mobius transformation w → w. In this case we have

so our Lorentz transformation reduces to t' = t, x' = x, y' = y, z' = z as expected. None of the points move on the complex plane, so none move on the Riemann sphere under stereographic projection, and nothing changes in the sky's appearance. Now let's consider the Mobius transformation w → –1/w. In this case we have

and so the corresponding Lorentz transformation is t' = t, x' = –x, y' = y, z' = –z . Thus the x and z coordinates have been reflected. This is certainly a proper orthochronous Lorentz transformation, because the determinant is +1 and the coefficient of t is positive. But does reflecting the x and z coordinates agree with the stereographic effect on the Riemann sphere of the transformation w → –1/w? Note that the point w = r + 0i maps to –1/r + 0i. There's a nice little geometric demonstration that the stereographic projections of these points have coordinates (x,0,z) and (–x,0,–z) respectively, noting that the two projection lines have negative inverse slopes and so are perpendicular in the xz plane, which implies that they must strike the sphere on a common diameter (by Pythagoras' theorem). A similar analysis shows that points off the real axis with projected coordinates (x,y,z) in general map to points with projections (–x,y,–z) points.

The two examples just covered were both trivial in the sense that they left t unchanged. For a more interesting example, consider the Mobius transformation w → w + p, which corresponds to the Lorentz transformation

If we denote our spacetime coordinates by the column vector X with components x₀ = t, x₁ = x, x₂ = y, x₃ = z, then the transformation can be written as Xʹ = LX where

To analyze this transformation, note first that we can decompose any Lorentz transformation into the product of a simple boost and a simple rotation. Let v₁, v₂, v₃ denote the components of the velocity of the origin of the Xʹ coordinate system in terms of the X coordinates, let v denote the magnitude v = (v₁² + v₂² + v₃²)^1/2, and let γ denote the "boost factor" γ = (1−v²)^−1/2. By inverting L and examining the expressions for x, y, z given xʹ = yʹ = zʹ = 0, we find that

Any matrix representing a transformation from the X coordinates to a system at rest with the Xʹ coordinates must have these values as the top row. In addition, if we want the velocity of the origin of the X coordinates to have the components –v₁, −v₂, −v₃ relative to the transformed coordinates, then the first column of the transformation matrix must have the same values as the first row. The L matrix does not satisfy this latter requirement. Therefore, if we define a "pure boost" as a Lorentz transformation between two inertial coordinate systems such that the two see each other moving with velocities (v₁,v₂,v₃) and (–v₁,–v₂,–v₃) respectively, then the L transformation is not a pure boost.

Still, we can clearly apply a pure boost from X to a system of coordinates whose spatial origin always coincides with the spatial origin of Xʹ, so this system can differ from Xʹ only by a pure spatial rotation. In general, if we spatially rotate X so the motion is along the x axis, apply a simple pure boost, and then spatially rotate back, we can construct a pure boost to a state of motion moving with any given velocity v₁,v₂,v₃. This leads to the unique pure boost

where Q = (γ–1)/v². Equating the elements of the top row with those of L, we can express the velocity components in terms of the Mobius parameter p

and

Thus we can write the pure boost part of L as

We know that our Lorentz transformation L can be written as this pure boost B followed by a pure spatial rotation R, i.e., L = RB, so we can compute the rotation R = LB⁻¹, which in this case gives

This represents a rotation about the yʹ axis through an angle of

The correspondence between the coefficients of the Mobius transformation and the Lorentz transformation described above assumes stereographic projection from the North pole to the equatorial plane. If instead we project from the North Pole of the Riemann sphere to a complex plane parallel to (but not necessarily on) the equator, and if the North Pole is at a height h above the plane, then every point in the plane is a factor of h further away from the origin than in the case of equatorial projection (h=1). Therefore, the transformation w → (aw+b)/(cw+d) on the equatorial plane maps to the transformation w → (a′w+b′)/(c′w+d′) where

It's also worth noting that the instantaneous aberration observed by an accelerating observer does not differ from that observed by a momentarily co-moving inertial observer. We're referring here to the null (light-like) rays incident on a point of zero extent, so this is not like a finite spinning body whose outer edges have significant velocities relative to their centers. We're just referring to different coordinate systems whose origins coincide at a given point in spacetime, and describing how the light rays pass through that point in terms of the different coordinate systems at that instant. In this context the acceleration (or spinning) of the systems make no difference to the answer. In other words, as long as our inertial coordinate system has the same velocity and orientation as the (ideal point-like) observer at the moment of the observation, it doesn't matter if the observer is in the process of changing his orientation or velocity. (This is a corollary of the "clock hypothesis" of special relativity, which asserts that a traveler's time dilation at a given instant depends only on his velocity and not his acceleration at that instant.)

In general, the effect of the finite Mobius transformation

for complex constants a,b,c,d can be classified according to the value of the "squared trace"

We call this the "conjugacy parameter", because two linear fractional transformations are conjugate if and only if they have the same value of σ. The different kinds of transformations are listed below:

                              0  ≤ σ  < 4                         elliptic

                                  σ = 4                              parabolic

                                  σ > 4                              hyperbolic

                            σ < 0 or not real                  loxodromic

We note that pure rotations (a special case of elliptic transformations) have the form

where an overbar denotes complex conjugation.

Iteration of the function f(z) generates the discrete sequence f₁(z) = f(z), f₂(z) = f(f(z)), f₃(z) = f(f(f(z))), and so on for all f_n(z) where n is a positive integer. It's not difficult to show that these iterates are cyclical with a period m if and only if σ = 4cos(2kπ/m)² for some integer k. We can also give an explicit expression for f_p(z) where p is any complex number. This effectively gives us the infinitesimal generator of the finite transformation. To accomplish this we must (in general) first map the discrete generator f(z) to a domain in which it has some convenient exponential form, then apply the pth-order transformation, and then map back to the original domain. There are several cases to consider, depending on the character of the discrete generator.

In the degenerate case when ad = bc with c ≠ 0, the pth iterate of f(z) is simply the constant f_p(z) = a/c. On the other hand, if c = 0 and a = d ≠ 0, then f_p(z) = z + (b/d)p. The third case is with c = 0 and a ≠ d. The pth iterate of f(z) in this case is

Notice that the second and third cases are really linear transformations, since c = 0. The fourth case is with c ≠ 0 and (a+d)²/(ad–bc) = 4, which leads to the following closed form expression for the pth iterate

This corresponds to the case when the two fixed points of the Mobius transformation are co-incident. In this "parabolic" case, if a+d = 0 then the Mobius transformation reduces to the first case with ad–bc = 0.

Finally, in the most general case we have c ≠ 0 and (a+d)² /(ad–bc) ≠ 4, and the pth iterate of f(z) is given by

where

This is the general case with two distinct fixed points. (If a+d = 0 then σ = 0 and K = –1.) The parameters α and β are the coefficients of the linear transformation that maps the real axis to the locus of points with real part equal to 1/2. Notice that the pth composition of f satisfies the relation

so we have

where

Thus h(f(z)) = K h(z), which shows that f(z) is conjugate to the simple function Kz. Since α+β is the complex conjugate of β, we see that h(z) can be expressed as

where

This enables us to express the pth composition of any linear fractional transformation with two fixed points, and therefore any corresponding Lorentz transformation, in the form

This shows that there is a particular oriented frame of reference (i.e., an orientation as well as velocity boost) represented by h(z), with respect to which the relation between the oriented frames z and f(z) is purely exponential.

Return to Table of Contents