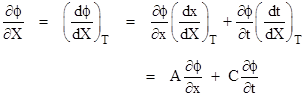1.4  The Relativity of Light

According to the theory of emission, the transmission of energy [of light] is effected by the actual transference of light-corpuscles… According to the theory of undulation, there is a material medium which fills the space between two bodies, and it is by the action of contiguous parts of this medium that the energy is passed on…

                                                                             James Clerk Maxwell

Light is arguably the phenomenon of nature with which we have the most conscious experience, by means of our sense of vision, and yet throughout most of human history very little seems to have been known about how vision works. Interestingly, from the very beginning there were at least two distinct concepts of light, existing side by side, as can be seen in some of the earliest known writings. For example, the description of creation in the biblical book of Genesis says light was created on the first day, and yet the sun, moon, and stars were not created until the fourth day “to give light upon the earth”. Evidently the word “light” is being used to signify two different things on the first and fourth days. For another example, Plato argued in Timaeus that there are two kinds of “fire” involved in our sense of vision, one coming from inside ourselves, emanating as visual rays from our eyes to make contact with distant objects, and another, which he called “daylight”, that (when present) surrounds the visual rays from our eyes and facilitates the conveyance of the visual images. These two kinds of “fire” correspond roughly with the later scholastic concepts of lux and lumen. The word lux was used to signify our visual sensations, whereas the word lumen referred to an external agent (such as light from the sun) that somehow participates in our sense of vision.

There was also, in ancient times, a competing theory of vision, according to which all objects naturally emit whole “images” (eidola) of themselves in small packets, and these enter our souls by way of our eyes. To account for our inability to see at night, it was thought that light from the sun or moon struck the objects and caused them to emit their images. This model of vision still entailed two distinct kinds of light: the facilitating illumination from the sun or moon, and the eidola emitted by ordinary objects. This somewhat awkward conception of vision was improved by Ibn al-Haitham and later by Kepler, who argued that it is not necessary to assume whole objects emit multiple copies of themselves; we can simply consider each tiny part of an object as the source of rays emanating in all directions, and a sub-set of these rays intersecting in the eye can be re-assembled into an image of the object.

Until the end of the 17th century there was no evidence to indicate that rays of light propagated at a finite speed, and they were often assumed to be instantaneous. Only in 1689 with Roemer’s observations of the moons of Jupiter, and even more convincingly in 1728 with Bradley’s discovery of stellar aberration, did it become clear that the rays of lumen propagate through space with a characteristic finite speed. This suggested that light, and the energy it conveys, must have some mode of existence during the interval of time between its emission and its absorption. Hence light became an entity or process in itself, rather than just a relation between entities, but again there were two competing notions as to the mode of existence. Two different analogies were conceived, based on the behavior of ordinary material substances. Some thought light could be regarded as a stream of material corpuscles moving through empty space, whereas other believed light consists of undulations or waves in a pervasive material medium. Each of these analogies was consistent with some of the attributes of light, but neither could be reconciled fully with all the attributes. For example, if light consists of material corpuscles, then according to Galilean relativity there should be an inertial reference frame with respect to which light is at rest in a vacuum, whereas in fact we never observe light in a vacuum to be at rest, nor even noticeably slow, with respect to any inertial reference frame. On the other hand, if light is a wave propagating through a material medium, then the constituent parts of that medium should, according to Galilean relativity, behave inertially, and in particular should have a definite rest frame, whereas we find that light propagates best through regions (vacuum) in which there is no detectable material with a definite rest frame, and again we cannot conceive of light at rest in any inertial frame. Thus the behavior of light defies realistic representation in terms of the behavior of material substances within the framework of Galilean space and time, even if we consider just the classical attributes, let alone quantum phenomena.

By the end of the 19th century the inadequacy of both of the materialistic analogies for explaining the behavior of light had become acute, because there was strong evidence that light exhibits two seemingly mutually exclusive properties. First, Maxwell showed how light can be regarded as a propagating electromagnetic wave, and as such the speed of propagation is obviously independent of the speed of the source. Second, numerous experiments showed that light propagates at the same speed in all directions relative to the source, just as we would expect for streams of inertial corpuscles. Hence some of the attributes of light seemed to unequivocally support an emission theory, while others seemed just as unequivocally to support a wave theory. In retrospect it’s clear that there was an underlying confusion regarding the terms of description, i.e., the systems of inertial coordinates, but this was far from clear at the time.

One of the first clues to unraveling the mystery was found in 1887, when Woldemar Voigt made a remarkable discovery concerning the ordinary wave equation. Recall that the wave equation for a time-dependent scalar field ϕ(x,t) in one dimension is

where u is the propagation speed of the wave. This equation was first studied by Jean d'Alembert in the 18th century, and it applies to a wide range of physical phenomena. In fact it seems to represent a fundamental aspect of the relationship between space, time, and motion, transcending any particular application. Traditionally it was considered to be valid only for a coordinate system x,t with respect to which the wave medium (presumed to be an inertial substance) is at rest and has isotropic properties, because if we apply a Galilean transformation to these coordinates, the wave equation is not satisfied with respect to the transformed coordinates. However, Galilean transformations are not the most general possible linear transformations. Voigt considered the question of whether there is any linear transformation that leaves the wave equation unchanged.

The general linear transformation between two coordinate systems X,T and x,t moving relative to each other with a given speed v is of the form

for constants A,B,C,D (which may be functions of v). If we choose units of space and time so that the characteristic speed u equals 1, the wave equation in terms of x,t coordinates is simply ∂²ϕ/∂x² = ∂²ϕ/∂t². We seek constants A,B,C,D (for a given relative velocity v between the coordinate systems) such that if f satisfies the wave equation in terms of x,t then it also satisfies the wave equation ∂²ϕ/∂X² = ∂²ϕ/∂T² in terms of X,T. To express the latter equation in terms of the x,t coordinates, recall that the total differential of ϕ can be written in the form

Also, at any constant T, the value of ϕ is purely a function of X, so we can divide through the above equation by dX to give

Taking the partial derivative of this with respect to X then gives

Since partial differentiation is commutative, this can be written as

Substituting the prior expression for ∂ϕ/∂X and carrying out the partial differentiations gives an expression for ∂²/∂X² in terms of partials of ϕ with respect to x and t. Likewise we can derive a similar expression for ∂²ϕ/∂T². Making use of these expressions, the wave equation  ∂²ϕ/∂X² = ∂²ϕ/∂T² can be written as

Since ϕ satisfies the equation ∂²ϕ/∂x² = ∂²ϕ/∂t², the above equation reduces to

The mixed partial derivative is not proportional to the second derivative with respect to x, so the coefficients of each individual terms must vanish. Thus the necessary and sufficient condition for ϕ to satisfy the wave equation in terms of the X,T coordinates (given that it satisfies the wave equation in terms of the x,t coordinates) is that the constants A,B,C,D of our linear transformation satisfy

Furthermore, the differential of the space transformation is dx = AdX + BdT, so an increment with dx = 0 satisfies dX/dT = −B/A. This represents the velocity v at which the spatial origin of the x,t coordinates is moving relative to the X,T coordinates. We also have the inverse transformation from (X,T) to (x,t):

Proceeding as before, the differential of this space transformation gives dx/dt = B/D for the velocity of the spatial origin of the X,T coordinates with respect to the x,t coordinates, and this must equal −v. Therefore we have B = −Av = −Dv, and so A = D. It follows from the condition imposed by the wave equation that B = C, so both of these equal −Av. Our transformation can then be written in the form

The same analysis shows that the perpendicular coordinates y and z of the transformed system must be given by

In order to make the transformation formula for x agree with the Galilean transformation, Voigt chose A = 1, so he did not actually arrive at the Lorentz transformation, but nevertheless he had shown roughly how the wave equation could actually be relativistic – just like the dynamic behavior of inertial particles – provided we are willing to consider a transformation of the space and time coordinates that differs from the Galilean transformation. Had he considered the inverse transformation

he might have noticed that the determinant is A²(1−v²), so to make this equal to 1 we must have A = 1/(1−v²)^1/2, which not only implies y = Y and z = Z, but also makes the transformation formally identical to its inverse. In other words, he would have arrived at a completely relativistic framework for the wave equation. However, this was not Voigt’s objective, and he evidently regarded the transformed coordinates x, y, z and t as merely a convenient parameterization for purposes of calculation, without attaching any greater significance to them.

Voigt’s transformation was the first hint of how a wavelike phenomenon could be compatible with the principle of relativity, which (as summarized in the preceding section) is that there exist inertial coordinate systems in terms of which free motions are linear, inertia is isotropic, and every material object is instantaneously at rest with respect to one of these systems. None of this conflicts with the observed behavior of light, because the motion of light is observed to be both linear and isotropic with respect to inertial coordinate systems. The fact that light is not at rest with respect to any system of inertial coordinates does not conflict with the principle of relativity if we agree that light is not a material object.

The incompatibility of light with the Galilean framework arises not from any conflict with the principle of relativity, but from the tacitly adopted empirical conclusion that two relatively moving systems of inertial coordinates are related to each other by Galilean transformations, so that the composition of co-linear speeds is simply additive. As discussed in the previous section, we aren't free to impose this assumption on the class of inertial coordinate systems, because they are fully determined by the requirement for inertia to be homogeneous and isotropic. There are no more adjustable parameters (aside from insignificant scale factors), so the composition of velocities with respect to relatively moving inertial coordinate systems is a matter to be determined empirically.

Recall from the previous section that, on the basis of slowly moving reference frames, Galileo and Newton had inferred that the composition of speeds was simply additive. In other words, if a material object B is moving at the speed v in terms of inertial rest frame coordinates of a material object A, and if an object C is moving in the same direction at the speed u in terms of inertial rest frame coordinates of B, then Newton found that object C has the speed v + u in terms of the inertial rest frame coordinates of A. Toward the end of the nineteenth century, more precise observations revealed that is not quite correct. It was found that the speed of object C in terms of inertial rest frame coordinates of A is not v + u, but rather (v + u)/(1 + uv/c²), where c is the speed of light in a vacuum.

These conclusions would be identical if the speed of light was infinitely great, which was still considered a possibility in Galileo's day. Many people, including Descartes, regarded rays of light as instantaneous. Even Newton's Opticks, published in 1704, made allowances for the possibility that "light be propagated in an instant" (although Newton himself was persuaded by Roemer's observations that light has a finite speed). Hence it can be argued that the principles of Galileo and Einstein are essentially identical in both form and content. The only difference is that Galileo assessed the propagation of light to be "if not instantaneous then extraordinarily fast", and thus could neglect the term uv/c², especially since he restricted his considerations to the movements of material objects, whereas subsequently it became clear that the speed of light has a finite value, and it was necessary to take account of the uv/c² term when attempting to incorporate the motions of light and high-speed particles into the framework of mechanics.

The empirical correspondence between inertial isotropy and lightspeed isotropy can be illustrated by a simple experiment. Three objects, A, B, and C, at rest with respect to each other can be arranged so that one of them is at the midpoint between the other two (the midpoint having been determined using standard measuring rods at rest with respect to those objects). The two outer objects, A and C, are equipped with identical clocks, and the central object, B, is equipped with two identical guns. Let the two guns in the center be fired simultaneously in opposite directions toward the two outer objects, and then at a subsequent time let object B emit a flash of light. If the arrivals of the bullet and light pulse coincide at A, then they also coincide at C, signifying that the propagation of light is isotropic with respect to the same system of coordinates in terms of which mechanical inertia is isotropic, as illustrated in the figure below.

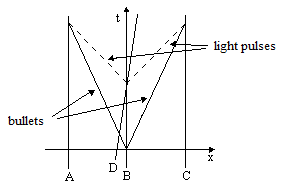
The fact that light emitted from object B propagates isotropically with respect to B's inertial rest frame might seem to suggest that the light pulses and the bullets can be treated as inertial objects within the Galilean framework. However, we also find that if the light is emitted at the same time and place from an object D that is moving with respect to B (as shown in the figure above), the light's speed is still isotropic with respect to B's inertial rest frame. This might seem to suggest that light is a disturbance in a material medium in which the objects A,B,C just happen to be at rest, but this is ruled out by the fact that it applies regardless of the state of (uniform) motion of those objects. The pulses of light propagate isotropically with respect to the inertial rest coordinates of object D as well. To demonstrate this, we could arrange for two other bodies, denoted by E and F, at equal distances on either side of D and moving at the same speed as D. Then we could fire identical bullets from two identically-constructed guns (at rest with respect to D) in opposite directions, toward E and F. The results are illustrated below.

The guns are fired from D at event e₁, and the bullets strike E and F at the events e₃ and e₄, coincident with the arrival of the light pulses emitted from D at event e₂. Obviously the time axis for the inertial rest frame coordinates of object D is the worldline of D itself (rather than the original "t" axis shown on the figure). In addition, since inertial coordinates are defined such that mechanical inertia is isotropic, it follows that the bullets fired from identical guns at rest with D are moving with equal and opposite speeds with respect to D's inertial rest coordinates, and since E and F are at equal distances from D, it also follows that the events e₃ and e₄ are simultaneous with respect to the inertial rest coordinates of D. Hence, not only is the time axis of D's rest frame slanted with respect to B's time axis, the spatial axis of D's rest frame is equally slanted with respect to B's spatial axis.

Several other important conclusions can be deduced from this figure. For example, with respect to the original x,t coordinate system, the speeds of the bullets from D are not given by simply adding (or subtracting) the speed of the bullets with respect to D's rest frame to (or from) the speed of D with respect to the x,t coordinates. Since momentum is explicitly conserved, this implies that the inertia of a body increases with it's velocity (i.e., kinetic energy), as is discussed in more detail in Section 2.3. We should also note that although the speed of light is isotropic with respect to any inertial spacetime coordinates, independent of the motion of the source, the light itself is not isotropic. The relationship between the frequency (and energy) of the light with respect to the rest frame of the emitting body and the frequency (and energy) of the light with respect to the rest frame of the receiving body does depend on the relative velocity between those two massive bodies (as discussed in Section 2.4).

Incidentally, notice that we can rule out the possibility of object B and D dragging the light medium along with them, because they are moving through the same region of space at the same time, and they can't both be dragging the same medium in opposite directions. This is in contrast to the case of (for example) acoustic pressure waves in a material substance, because in that case a recognizable material substance determines the unique isotropic frame, whereas in the case of light we're unable to identify any definite material medium, so the medium has no definite rest frame.

The first person to discern the true relationship between relatively moving systems of inertial coordinate systems was Hendrik Antoon Lorentz. Not surprisingly, he arrived at this conception in a rather indirect and laborious way, and didn't immediately recognize that the class of coordinate systems he had discovered (and which he called "local coordinate" systems) were none other than Galileo's inertial coordinate systems. Incidentally, although Lorentz and Voigt knew and corresponded with each other, Lorentz apparently was not aware of Voigt’s earlier work on coordinate transformations that leave the wave equation invariant, and so that work had no influence on Lorentz’s search for coordinate systems in terms of which Maxwell’s equations are invariant. Unlike Voigt, Lorentz derived the transformation in two separate stages. He first developed the "local time" coordinate, and only years later came to the conclusion (after, but independently of, Fitzgerald) that a "contraction" of spatial length was also necessary in order to account for the absence of second-order effects in Michelson's experiment.

Lorentz began with the absolute ether frame coordinates t and x, in terms of which every event can be assigned a unique space-time position (t,x), and then he considered a system moving with the velocity v in the positive x direction. He applied the traditional Galilean transformation to assign a new set of coordinates to every event. Thus an event with ether-frame coordinates t,x is assigned the new coordinates xʺ = x - vt and tʺ = t. Then he tentatively proposed an additional transformation that must be applied to xʺ,tʺ in order to give coordinates in terms of which Maxwell's equations apply in their standard form. Lorentz was not entirely clear about the physical significance of these “local” coordinates, but it turns out that all physical phenomena conform to the same isotropic laws of physics when described in terms of these coordinates. Taking units such that c = 1, letting g = 1/(1−v²)^1/2, and omitting a constant factor that Lorentz later determined to be 1, his equations for the local coordinates xʹ and tʹ in terms of the Galilean coordinates which we are calling xʺ and tʺ are

Recall that the traditional Galilean transformation is xʺ = x − vt and tʺ = t, so we can make these substitutions to give the complete transformation from the original ether rest frame coordinates x,t to the local coordinates moving with speed v

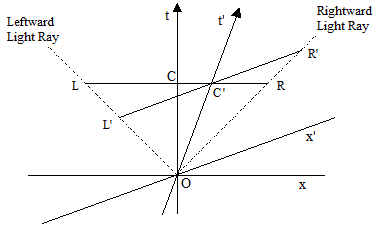
These effective coordinates enabled Lorentz to explain how two relatively moving observers, each using his own local system of coordinates, both seem to remain at the center of expanding spherical light waves originating at their point of intersection, as illustrated below

The x and xʹ axes represent the respective spatial coordinates (say, in the left/right direction), and the t and t' axes represent the respective time coordinates. One observer is moving through time along the t axis, and the other has some relative rightward velocity as he moves through time along the t' axis. The two observers intersect at the event labeled O, where they each emit a pulse of light. Those light pulses emanate away from O along the dotted lines. Subsequently the observer moving along the t axis finds himself at C, and according to his inertial measures of space and time the outward going light waves are at L and R at that same instant, which places him at the midpoint between them. On the other hand, the observer moving along the t' axis finds himself at point Cʹ, and according to his inertial measures of space and time the outward going light waves are at Lʹ and Rʹ at this instant, which implies that he is at the midpoint between them.

Thus Lorentz discovered that by means of "fictitious" coordinates such as xʹ,tʹ it was possible to conceive of a class of relatively moving coordinate systems with respect to which the speed of light is invariant. He went beyond Voigt in the realization that the existence of this class of coordinate systems ensures the appearance of relativity, at least for optical phenomena, and yet, like Voigt, he still tended to regard the "local coordinates" as artificial. Having been derived specifically for electromagnetism, it was not clear that the same transformations should apply to all physical phenomena, including inertia, gravity, and whatever forces are responsible for the stability of matter – at least not without simply hypothesizing this to be the case. However, Lorentz was dissatisfied with the proliferation of hypotheses that he had made in order to arrive at this theory. The same criticism was made in a contemporary review of Lorentz's work by Poincare, who chided him with the remark "hypotheses are what we lack least". The most glaring of these was the hypothesis of contraction, which seemed distinctly "ad hoc" to most people, including Lorentz himself originally, but gradually he came to realize that the contraction hypothesis was not as unnatural as it might seem.

Surprising as this hypothesis may appear at first sight, yet we shall have to admit that it is by no means far-fetched, as soon as we assume that molecular forces are also transmitted through the ether, like the electric and magnetic forces…

He set about trying to show (admittedly after the fact) that the Fitzgerald contraction was to be expected based on what he called the Molecular Force Hypothesis and his theorem of Corresponding States, as discussed in the next section.

Return to Table of Contents