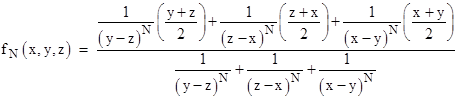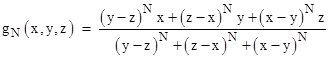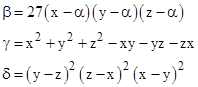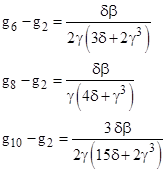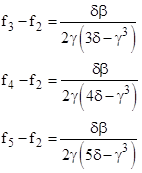|
Trivariate Functions |
|
|
|
For any given N, consider the trivariate function |
|
|
|
|
|
|
|
and the somewhat related function |
|
|
|
|
|
|
|
As noted in an article on inverse-square interpolation, these two functions are identical with N=2, meaning that we have |
|
|
|
|
|
|
|
but this identity does not apply for any other value of N. Two somewhat surprising identities are |
|
|
|
|
|
|
|
We also have |
|
|
|
|
|
|
|
We define α = (x+y+z)/3. To describe some of the relations between these functions, it’s useful to define the following auxiliary functions |
|
|
|
|
|
|
|
In these terms we have, in addition to g4 − g2 = 0, the following identities (omitting the arguments for convenience) |
|
|
|
|
|
|
|
From these we can infer the relations |
|
|
|
|
|
|
|
Thus both g5 and g7 are just weighted averages of g2 and the average of the arguments. We can also verify the following identities involving the g functions |
|
|
|
|
|
|
|
and the similar identities involving the f functions |
|
|
|
|
|
|
|
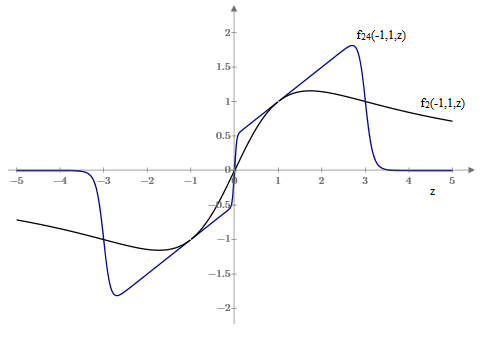
The behavior of the f functions can be seen in the plot below, which shows fN(−1,1,z) with x = −1, y = 1, and N=2 or N=24. |
|
|
|
|
|
|
|
This shows that, for large values of N, the function approaches the average of the two arguments that are closest together. Thus for z less than −3 the function equals zero, being the average of x = −1 and y = +1), but when z exceeds −3 the function jumps to the average of x and z, until z reaches zero, at which point the function jumps to the average of y and z, until z reaches 3, at which point the function jumps back to zero (the average of x and y). |
|
|
|
For purposes of interpolation we typically want to avoid not only step changes, but any extreme sensitivities. In other words, a small change in one of the arguments shouldn’t produce a greatly amplified change in the function. This is one reason the case N=2 is often preferred. Note that for any given x and y we have df2/dz = 4/3 at the most sensitive value of z, which occurs at z = (x+y)/2. Thus the maximum amplification is fairly mild. |
|
|
|
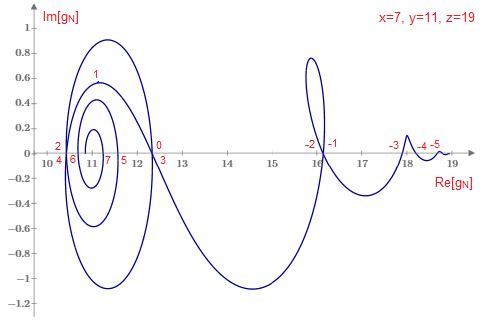
We can also extend the definition of the gN(x,y,z) function to include real values of N, not restricted to integers. For any given values of the arguments x,y,z this results in an interesting complex function of N, as illustrated below for the case x=7, y=11, z=19. |
|
|
|
|
|
|
|
This shows the locus of real and imaginary parts of gN(7,11,19) for N ranging continuously from −5 to +7. The value is purely real whenever N has an integer value, with the exception of the removable singularity at N=1, as shown by the values of N shown next to the locus in the figure. As N increases, the value of gN goes to the middle argument (in this case, 11), whereas as N becomes progressively more negative the value of gN goes to either the largest or smallest argument (in this case, 19), whichever is further from the middle argument. |
|
|