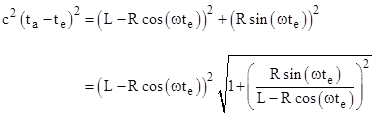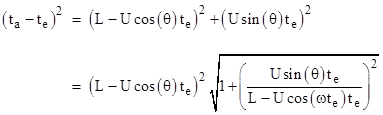Superluminal or Not

Yea, though I walk through the valley of the shadow

of death, I will fear no evil, for thou art with me...

                                                                 Psalms 23:4

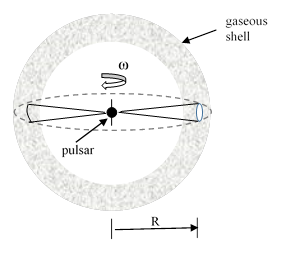
Consider a pulsar surrounded by a roughly spherical shell of particles or gas. As the pulsar rotates, it emits beams of synchrotron radiation in both directions along its magnetic axis, and these beams illuminate two regions in the surrounding spherical shell. Those “spots” revolve around the pulsar, and depending on the rotation rate of the pulsar and the radius of the shell of material, it is quite possible for the illuminated spots to be moving at superluminal speeds (just as it’s possible for a shadow to move faster than light). This doesn’t violate relativity, because no information or energy is moving faster than light. The “moving spot” is really just a coordinated sequence of illumination events. This is depicted in the figure below.

In this situation, each illuminated region of the gaseous shell would be “moving” in a circle of radius R and angular frequency of ω, so the speed of this illuminated region is V=ωR. As noted above, V can easily exceed c (the speed of light in vacuum). In terms of rectangular coordinates x,y in the plane of rotation and centered on the pulsar, the position of one of the illuminated regions can be written as

where t is the inertial time coordinate associated with x,y. The illuminated region will be a source of light, either through stimulated emission or reflection. Successive emission events will be space-like separated if V exceeds c. The appearance of this light to a distant observer (in the plane of rotation) can be inferred from the figure below.

Letting t_e and t_a denote the times of emission and absorption (respectively) of a pulse of light from the illuminated region, we have the relation

For sufficiently large L in comparison with R the expression under the radical approaches 1, so that factor is negligible, and we have

The last term on the right side is just the constant nominal time to travel the distance L, so we can omit that, since we are only interested in the pattern of receptions. Thus we have

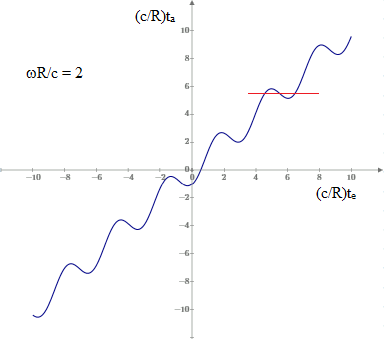
A plot of the scaled values of the absorption time t_a versus the corresponding values of emission times t_e for the case ωR/c = 2 is shown below.

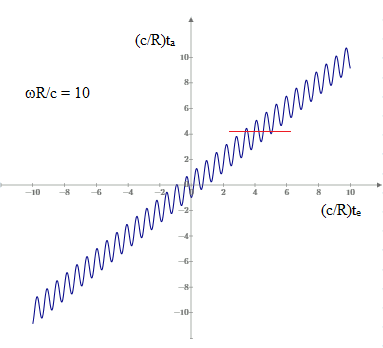
Notice that a given absorption time can correspond to three different emission times, so the spectral analysis would show a signature of the illuminated region of the gas cloud from three different emission events. For larger values of ωR/c we can have any number of such “apparitions”. For example, the plot below shows the scaled values of t_a versus t_e with ωR/c = 10, and we can have up to seven emission events visible at any given reception time.

This effect is formally very similar to the effect for which de Sitter searched in 1913 by examining binary star systems, although he was not looking for reflected or stimulated sources moving at superluminal speeds, he was examining the direct light from the components of binary star systems, searching for evidence to prove that the propagation of light is independent of the speed of the source. If the speed of light from the components was c+v (as it would be in an emission theory), where v was the speed of the star at any given time, then we would expect to see multiple images. De Sitter found no evidence for such apparitions, nor was any found in 1977 when the observations were repeated in the x-ray range to address the possibility that “extinction” in the interstellar gases might alter the speed of light in transit. This is evidence that the speed of light in vacuum is indeed independent of the speed of the source.

But the effect we are discussing here is quite different, since we are considering reflected or simulated emissions from “sources” that are actually superluminal, in the sense that successive emission source events are spacelike separated. We wouldn’t expect to see this effect in the light from binary star systems. The best opportunity would probably be from a gaseous shell of matter surrounding a pulsar, as discussed above.

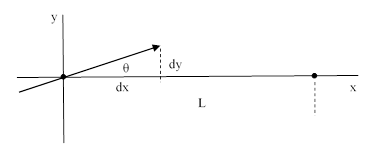
People sometimes confuse this effect with the so-called “superluminal jet”, but that’s actually a completely different phenomenon. In that case the source of light is moving subluminally, and there are no multiple apparitions, but the received signals are misinterpreted, leading to the mistaken conclusion that the source is moving superluminally. This is easily explained by referring to the figure below.

For convenience we will work in units such that c=1. A jet of luminous material is passing through the origin at the speed U, making an angle of θ with the x axis. The receiver is located at x = L. The x and y coordinates of the emission event at time t_e are

Note that the right hand expression gives dy_e/dt_e = Usin(θ). The relationship between the emission and absorption times is

For sufficiently large L in comparison with Ut_e, the quantity inside the radical approaches 1, so we can neglect that factor, which leaves us with

Therefore we have

Combining this with the expression for dy_e/dt_e, we get

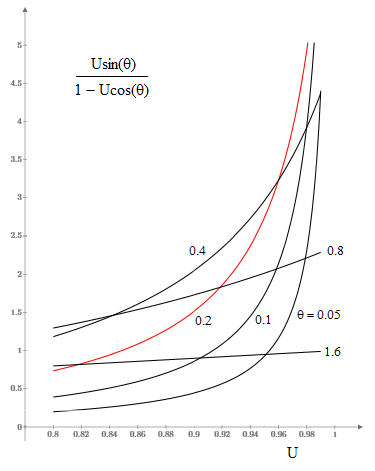
The receiver might (mistakenly) interpret this as the speed of the jet in the y direction, because this is how far the image moves in the direction per unit time at the receiver. However, this is not actually the speed of the jet, because the images are arriving at the receiver in compressed time, for the same reason that the frequency of the light is blue-shifted, due to the motion of the source toward the receiver. If U is close to the speed of light, and θ is small, this can result in values of dy_e/dt_a that exceed 1 (i.e., the speed of light), even though the jet is moving only at speed U. The figure below shows the values of dy_e/dt_a for various values of U and θ.

For example, if the jet speed is U = 0.96 and the angle is θ = 0.2 radians, the value of dy_e/dt_a is 3.22, so it might appear as if the jet was moving in the y direction with a speed more than 3 times the speed of light, but this is merely due to the failure to take into account the Doppler effect for a jet that is moving at high speed toward the receiver.

Return to MathPages Main Menu