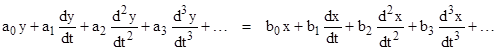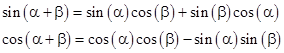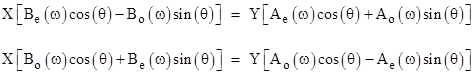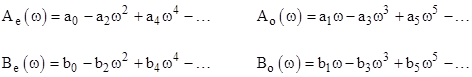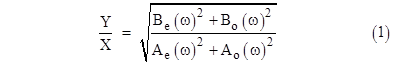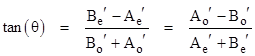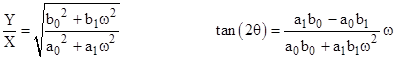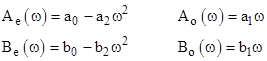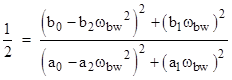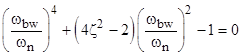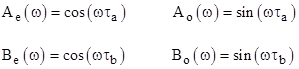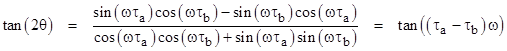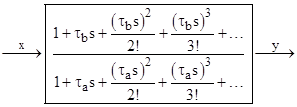Frequency Response of High-Order Systems

A thief, sentenced to the gallows for poaching on the King's land, bargains for his life by offering to teach the King's horse to talk in a year. To a skeptical friend the thief confides his hopes to avoid hanging: "Before the year is up, the horse may die, or the King may die, or I may die... or the horse may talk".

                                                                                                                Tudor joke

Consider two variables x and y related by the ordinary differential equation

where the coefficients a_j and b_j are constants. The relation is symmetrical, but we may regard x as the independent (input) variable and y as the dependent (output) variable. To determine the frequency response, we stipulate that x(t) and y(t) are both sinusoidal functions with the same frequency ω, but with different amplitudes X and Y, and with phases that differ by 2θ. Thus we can write these functions as

Substituting these functions into the preceding equation, and making use of the trigonometric identities

we arrive at an equation of the form

which can be satisfied by setting F(ω,θ) = 0 and G(ω,θ) = 0. This leads to the two equations

where

(The subscripts and A and B denote even and odd.) Dividing through each of the preceding two equations by Xcos(θ) and solving each of then for tan(θ), we get

Equating these two expressions for tan(θ), we arrive at the following relation between the amplitude ratio and the frequency

If we define normalized A functions as

and similarly for the normalized B functions, we can substitute for Y/X into the previous expressions for tan(θ) to give

Recalling that the full phase shift is 2θ, we can make use of the identity tan(2θ) = 2tan(θ)/[1−tan(θ)²] to show that the tangent of the full phase shift is

For a simple example, consider the first-order lead-lag transfer function, for which the only non-zero coefficients of the original differential equation are a₀, b₀, a₁, and b₁. In that case we have A_e = a₀, A_o = a₁ω, Be = b₀, and B_o = b₁ω, so the amplitude ratio and phase shift are given by equations (1) and (2) as

consistent with the results in the note on Lead-Lag Frequency Response. (In that note θ was defined as the full phase angle shift, whereas here it denotes half of the shift.)

Equation (1) can also be used to determine the bandwidth of a system, defined as the frequency at which the squared amplitude ratio equals 1/2. (This corresponds to the half power condition, since power is proportional to the square of the amplitude.) For example, a second-order system has the functions

so according to equation (1) the bandwidth frequency ω_bw satisfies the relation

Clearing fraction and collecting on the frequency, this can be written as

We can easily solve this quadratic equation for ω_bw². In the special case of a unitary transfer function with no numerator dynamics, we have b₁ = b₂ = 0, and a₀ = b₀ = 1, and we can also set a₂ = 1/ω_n² and a₁ = 2ζ/ω_n where ω_n is the natural frequency and ζ is the damping ratio. Making these substitutions, the condition on the bandwidth is

Solving this leads to the well-known expression for the bandwidth of such a system

For a higher-order example, consider the system defined by the original differential equation with the coefficients given by

where τ_a and τ_b are constants with units of time. In this case we have

and therefore Y/X = 1 and

Thus there is no attenuation of the amplitude, and the output phase lags the input by (τ_a – τ_b)ω, so conventionally we say the output is delayed in time by τ_a – τ_b. This is consistent with the fact that the transfer function represented by the original differential equation with these coefficients can be depicted in operator notation as

Recognizing that the numerator and denominator are just exponential functions, this is equivalent to the transfer function

which is a pure “time shift”, as discussed in the note on Transfer Functions and Causation.

Return to MathPages Main Menu