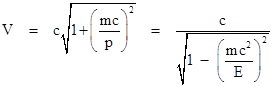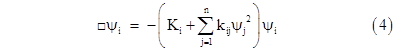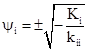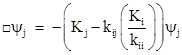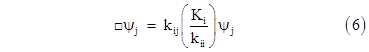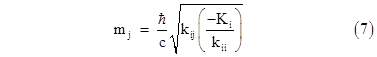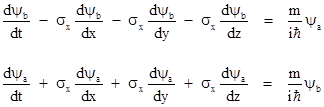On the Higgs Mechanism

Most popular explanations of the Higgs mechanism refer to entities moving through a substantial medium, such as molasses, a crowd of people, or a mist of steam. It’s easy to see how a massless particle (e.g., a photon) that moves at the speed c in vacuum could move at some lower average speed when negotiating its way through such a medium. Indeed the ordinary refraction of light in water or glass is an example of this phenomenon. Since the energy of a photon is propagating (on average) at a speed less than c in a refractive medium, there exists a system of inertial coordinates in which the photon’s energy is at rest, so we could say it has acquired a rest mass due to its interaction with the medium. However, these explanations involve a medium with a particular rest frame, whereas the actual Higgs mechanism is attributed to a relativistic field with no distinguished rest frame. It is natural to wonder, then, how a massless particle with no preferred rest frame can interact with a non-mechanistic field which also has no preferred rest frame and produce an effectively massive particle with a preferred rest frame. Most popular explanations of the Higgs mechanism don’t really address this crucial question. To provide a genuine explanation, it’s necessary to describe scalar fields and how quantum particles interact with such fields.

In quantum field theory a particle is an excitation of a quantum field. The classical wave equation for a continuous scalar field ψ(t,x,y,z) is of the form

where K is a constant. (Most fields in nature have multiple components, like the electric and magnetic components of the electromagnetic field, so they are not actually scalar fields, but their individual components satisfy formally similar equations, so we will simplify the discussion by focusing on scalar fields.) The expression on the left side is called the D’Alembertian of the function ψ, and is sometimes denoted by □ψ. Thus we can write the above equation as

This is known as the Klein-Gordon equation. In a sense, we might say the scalar constant K is formally an eigenvalue of the D’Alembert operator, and the field ψ is a corresponding eigen function. A plane wave propagating in the x direction at the speed V = ω/k would be of the form ψ = ψ₀ sin(kx−ωt) for some constant amplitude ψ₀, and so, inserting this into the wave equation, we get the condition

If K = 0 we have V = c, meaning that the phase velocity equals the speed of light, so this field disturbance corresponds to a massless particle. On the other hand, if the constant K has the value

where ℏ (= h/2π) is Planck’s constant and m is some non-zero constant, then we have

Recalling that E = ℏω and p = ℏk this can be written as

which of course is the relativistic energy-momentum relation for a particle of rest mass m. The phase speed V = ω/k = E/p is given by

This shows that as the momentum of the particle goes to zero, the phase speed V goes to infinity. However, the group velocity v of a disturbance is not equal to ω/k but rather dω/dk. Taking the total differential of (2), we find that v = c²/V, and therefore by substituting for V into the preceding expressions and solving for p and E we have

which of course are the relativistic expressions for momentum and energy of a particle of rest mass m moving at the speed v.

In summary, equation (1) has two distinct cases to consider. If the constant K is zero, then the energy E and scaled momentum cp of any excitation of the field are equal, and such an excitation corresponds to a massless particle propagating at the speed of light (phase and group speeds are equal). On the other hand, if K has a non-zero (positive) value, any excitation of the field has energy that exceeds its scaled momentum, in accord with equation (3), and corresponds to a matter wave whose phase velocity V exceeds the speed of light and whose group velocity v is less than the speed of light, such that vV = c². We may surmise that, since a massive particle has energy that exceeds its scaled momentum, it must possess one or more intrinsic modes of energy.

Equation (1) seems to give a satisfactory account of individual quantum fields and their excitations (i.e., particles), but it does not entail any coupling between fields, so if that equation were exactly correct there would be no interactions between particles. However, we find that for any two fields, denoted by ψ₁ and ψ₂, the governing equations are actually coupled as shown below.

The symbols k₁₂ and k₂₁ are (equal) positive constants, representing the coupling strength between these two fields. If k₁₂ = 0 then the fields ψ₁ and ψ₂ do not interact.

More generally, given n fields denoted by ψ₁, ψ₂, ψ₃, … ψ_n, for every pair ψ_i and ψ_j we have a specified coupling constant k_ij (= k_ji). To account for the possibility of interactions, the governing equation (1) is modified to include these interaction contributions on the right side as follows.

The expression in parentheses may be considered the more general mass factor, replacing just the constant K_i in equation (1). In effect, the mass of the excitations of ψ_i has contributions not just from the original mass factor K_i but from the interaction terms as well.

The simplest case is for a field ψ_i with K_i = 0, and we can consider the field in isolation so that no other fields are present. In that case the right hand side vanishes, and we are left with just the homogeneous wave equation □ψ_i = 0, which has the steady-state solution ψ_i = 0. Any disturbances propagating in such a field will ordinarily be quite small in magnitude, and the squares of such disturbances would be much smaller still. Therefore, the summations on the right side of the governing equations would be extremely small, even in the presence of disturbances of other fields of this type. Thus, all particles would be essentially massless and propagate at the speed of light.

Now suppose there exists a field ψ_i with positive K_i. As discussed above, an excitation of this field would correspond to a massive particle, propagating at a (group) speed below the speed of light. Nevertheless, the equation □ψ_i = −K_iψ_i still has the steady-state solution ψ_i = 0, even with non-zero K_i, and any disturbances would be small fluctuations around zero – and their squares even smaller – so it seems that the summation in equation (4) would never contribute appreciably. Thus it might appear that quantum particles could have appreciable rest masses only due to their intrinsic K_i factors, and not due to any interactions.

However, there is one remaining case to consider. Suppose there exists a field ψ_i with non-zero K_i and with a non-zero self-interaction coefficient k_ii. Such a field, in isolation, satisfies the equation

At steady state the left side vanishes, and this equation is satisfied if either of the factors on the right hand side vanish. One solution is ψ_i = 0, but there are also two other solutions, given by the two roots of the quadratic factor in parentheses, namely

To determine which of these solutions is applicable, we need to examine how the potential energy ϕ of the field depends on the strength of the field. If we identify the right side of (5) with the negative partial derivative −∂ϕ/∂ψ_i, then the potential has the quartic form

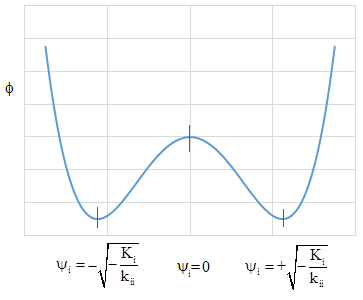
With a suitable negative value of K_i and positive k_ii, this function has three extrema (at the three roots of the right side of (5)) as shown in the figure below.

Consequently, although any of the three roots of the right side of (5) is formally a possible steady-state value for the field, the zero solution is unstable, because the slightest perturbation will cause the field to slide down to one of the lower energy states on either side. Actually, since ψ_i is allowed to be complex, we should draw a three-dimensional picture, resembling a “Mexican hat”, with the energy trough surrounding the central hill. The stable solutions are such that the absolute value (norm) of the complex number ψ_i equals the square root of –K_i/k_ii.

Given the existence of one field ψ_i with negative K_i and positive k_ii, the governing equation (5) for any other field ψ_j with non-zero k_ij will have an appreciable contribution to its effective mass due to the coupling with the ψ_i field. In the absence of excitations in any other fields, the governing equation for the ψ_j will be

This shows that excitations of a field ψ_j with K_j = 0 could nevertheless exhibit an effective rest mass due entirely to their interaction with the special field whose steady-state value is non-zero as described above. In other words, the wave equation for the “ordinary” fields could be

where K_i is negative. Comparing this with equation (1), we see that excitations of the field ψ_j propagate like particles with an effective rest mass of

due to the interaction between the ψ_j field and the special ψ_i field.

According to the standard model of particle physics, most of the fundamental particles in nature that we normally regard as having rest masses, such as leptons and quarks, are excitations of fields whose governing equations have K_j = 0 and k_jj = 0, so the particles would be massless by themselves. The particles have an effective mass only because of the existence of one special field, called the Higgs field, whose governing equation has a negative K_i and positive k_ii. As explained above, these special characteristics cause the Higgs field to have a non-zero value in steady state (unlike all other fields, whose quiescent values are zero), and hence the excitations of any field ψ_j that couples with the Higgs field (i.e., such the coupling constant k_ij is non-zero) will propagate like a particle with the effective rest mass given by the expression above.

The Higgs field itself can also be excited, and such an excitation propagates as a massive particle called the Higgs boson. (In July 2012 CERN reported what is thought to be the first experimental detection of the Higgs boson at the Large Hadron Collider.) It may be worth noting that the mass of the Higgs particle is not entirely due to the interaction with the Higgs field, because it has a non-zero (albeit negative) “mass factor” K_i. It is conceivable that there exists more than one “Higgs-type field”. This is still under experimental investigation.

We should also mention that the Higgs field interactions are not the cause of all (or even most) of the mass that we encounter when dealing with ordinary macroscopic objects. As discussed above, an object exhibits rest mass if its energy E exceeds its scaled momentum cp. Consequently, whenever some quantity of energy is contained and prevented from propagating (macroscopically) at the speed c, the configuration has rest mass. For example, a photon bouncing around inside a box with mirrored internal walls is microscopically massless and propagates at c as it travels from wall to wall, but the photon’s energy contained within the box contributes to the rest mass of the stationary box. Likewise the mass of an atom is not just the sum of the microscopic rest masses of the constituent elementary particles, it also has contributions from the bound kinetic energies of those particles, as well as the binding energies. Thus it would be more accurate to say that all rest mass arises from mechanisms that constrain configurations of energy, preventing them from propagating (at least macroscopically) at the speed of light, which implies that they are (at least macroscopically) stationary in some inertial frame. The Higgs interaction is just one such mechanism, albeit one that operates on perhaps the most fundamental level.

From this point of view the workings of the Higgs mechanism may seem somewhat puzzling, because it is fundamentally different from, say, a mirrored box. We can easily understand how massless photons propagating at c inside the box are confined by reflections at the walls so that they are macroscopically stationary in the rest frame of the box. In this case the material box establishes a rest frame, and the photons are interacting with something that already has a rest frame. In contrast, the Higgs field does not have a rest frame; it is a Lorentz invariant and essentially constant scalar field. (Of course, each Higgs particle has a rest frame, but the quiescent Higgs field itself does not.) One might think that the potential energy of the non-zero quiescent Higgs field must either be propagating at c or else have a rest frame, but potential energy is inherently an interactive effect that has no mode of existence independent of how other entities (intrinsic mass-energy) behave.

Even if we were previously unacquainted with the Dirac equation, these considerations might have led us to suspect that most elementary quantum fields have multiple components that would individually be massless and propagate at c, but that are mutually coupled together in a bound configuration of energy that possesses a rest frame. According to this view, the Higgs field merely facilitates the coupling between the different modes of the particle. Recall that neutrinos were originally thought to be massless, propagating at the speed of light, but their non-zero rest mass was inferred from the discovery that neutrinos oscillate between distinct states. Likewise the mass of an electron (for example) can be associated with the coupling between the two 2-spinor components of Dirac’s model. As discussed in the article on the Dirac equation, by factoring the quadratic Klein-Gordon equation into two linear factors, we can write the equation for a spin-1/2 particle in terms of two coupled 2-spinor components ψ_a and ψ_b that individually satisfy the linear equations (in units with c = 1)

where the symbols σ_x, σ_y, and σ_z signify the 2x2 Pauli spin matrices. Each of the components still individually satisfies the Klein-Gordon equation, but the equations above show that we can regard the electron as consisting of two parts, each of which serves as the “source” for the other, with the constant m serving as the coupling coefficient. In this sense, we could say that each of these components without the other would be massless and propagate at c, but the two threads are woven together into a single massive particle. The total energy exceeds the scaled macroscopic momentum because of the energy involved in the intrinsic oscillations that don’t contribute to the macroscopic momentum.

In the standard model, the coupling coefficient m in these equations is due to the coupling with the non-zero Higgs field, as described previously. One of the motivations for this model is the desire for maximal symmetry between the various physical fields and particles. By attributing the effective rest masses of leptons and quarks to interactions with the Higgs field, rather than to intrinsic mass factors, we can conceive of rest mass as arising from a “broken symmetry” of the “Mexican hat” potential. In extremely hot conditions (such as are thought to have existed in the first fraction of a second after the “big bang”), the symmetry would not be broken, and all particles would be essentially massless.

Return to MathPages Main Menu