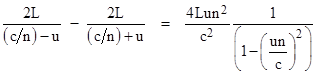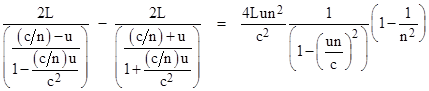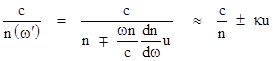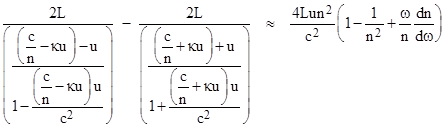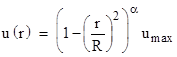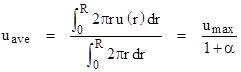Fresnel’s Drag Coefficient and Dispersion

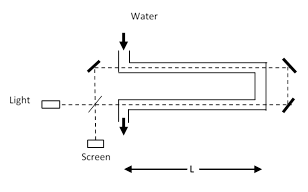
In 1851 an experiment was performed by the French physicist Hippolyte Fizeau to investigate the degree to which the propagation of light through a transparent medium is affected (if at all) by the motion of that medium. He chose water as the medium, and arranged for beams of light to propagate upstream and downstream through columns of water flowing in a set of tubes, as depicted schematically below.

Light is emitted from the source and then split into two beams by a half-silvered mirror. One beam proceeds clockwise around the rectangular path (and hence in the direction of the water flow) while the other beam proceeds counter-clockwise (and hence in the opposite direction of the water flow). If the speed of light is affected by the motion of the medium, going faster with the water than against, then it will take the two beams different amount of time to traverse the path, and the beams with interfere when re-combined a viewed on the screen. This will result in the appearance of a “fringe shift” proportional to the difference in travel times.

The two main conceptual models for light propagation at the time of Fizeau’s experiment were (1) waves in an ether theory, and (2) ballistic particles in an emission theory. In each of these theories there was uncertainty about how light passing through a transparent substance would be affected by the motion of the substance. Some proponents of the ether theory argued that the ether is perfectly motionless and unaffected by ordinary substances, while others believed the ether would be dragged along – either totally or partially – by the material medium. Similarly some proponents of emission (ballistic) theories imagined that particles of light pass freely through a transparent substance, whereas others pointed out that in order to account for different indices of refraction we must posit an “extinction” effect, such that the corpuscles of light are absorbed and re-emitted by the particles of the substance, and hence the light acquires its characteristic speed relative to the substance. Consequently, an emission theory with rapid extinction predicts the same propagation speed as an ether theory with complete convection.

The amount of convection (for an ether theory) or extinction (for an emission theory) was unknown, so experiments such as the one performed by Fizeau were designed to determine how much (if at all) the propagation speed of light in a transparent medium was affected by the motion of the medium. Notice that Newtonian physics didn't assume the light would be dragged along with the water, but it did assume that the overall speed of light in the lab frame must equal the sum of the speed of the water in the lab frame plus the speed of the light in the water frame. In other words, if the water is moving with speed u in the lab frame, and the light is moving with speed v in the water frame, then Newton assumed the light is moving with speed u+v in the lab frame. Thus, although the experiments were designed to test the various assumptions about how much (if at all) the light propagation speed was affected by the motion of the medium, they ended up revealing a more surprising fact about nature, namely, that the more basic Newtonian assumption of simply additive compositions of speeds (in terms of inertial coordinate systems) was untenable.

To explain this, first recall that in any material substance the index of refraction is defined as n = c/v, where c is the speed of light in vacuum and v is the speed of light in the material. The speed v is implicitly assumed to be the speed of light relative to the rest frame of the medium. This is equivalent to the assumption of complete convection for an ether theory and complete extinction for an emission theory. On this basis we can say light moves in Fizeau’s apparatus at the speed v = c/n relative to the rest frame of the water. Of course, the index of refraction is usually dependent on frequency, so we have to be sure to use the value of n corresponding to the frequency of light in the rest frame of the water, which in general differs from the frequency in the lab frame, due to the Doppler effect. We will start by assuming a non-dispersive medium, i.e., a medium in which the index of refraction is independent of frequency, so that the Doppler shift has no effect on the result. Later we will show how the equations need to be modified to account for dispersive media.

Since the light paths outside the water columns are identical, the difference in travel times for the clockwise and counter-clockwise light rays is just equal to the difference in times to traverse the columns of water. Based on the assumptions stated above, the speed (in water) of the light in the clockwise direction is c/n + u, and the speed in the opposite direction is c/n – u, so the difference in travel times is

Since u is extremely small compared to c, the time difference based on these assumptions is essentially just 4Lun²/c². The fringe shift δ is equal to the time difference multiplied by c/λ where λ is the wavelength of the light, so, to the first order in u/c, the predicted fringe shift based on the assumption of complete convection is

However, when the experiment is performed we do not get this result. From the standpoint of special relativity this is not surprising, because the above formula assumes simply additive composition of speeds (in terms of inertial coordinate systems), whereas according to special relativity the composition of v and u is not v+u, as Newton would have expected, but rather (v+u)/(1 + vu/c²). Therefore, for the case described above we ought to expect the time difference

This differs from the previous result by the factor 1 – 1/n². Multiplying by c/λ and again omitting terms higher than first order in u/c, the predicted fringe shift (assuming n is the applicable index of refraction) is

Already in 1818 Augustin Fresnel had inferred the extra factor of 1 – 1/n², which is commonly called the Fresnel drag (or convection) coefficient, to account for Arago’s observations of stellar aberration when viewed through a prism. He interpreted it as signifying the fraction of the velocity of the medium that is imparted to the putative luminiferous ether. However, there are significant problems with this interpretation, not least of which is the fact that the index of refraction of real material substances is, in general, dependent on the frequency of light, so we need infinitely many ethers, one for each frequency, each dragged along at a different rate. This was never considered very plausible, but the factor was nevertheless quite successful in accounting for various optical phenomena. Fizeau’s experiment in 1851 used an apparatus of length L = 1.487 m, with water velocity of u = 7.059 m/sec, and light with wavelength (5.26)10^–7 m. Noting that the index of refraction of water is N = 1.333, the predicted fringe shift given by (1) for complete convection is d = 0.4732, whereas the shift predicted by (2) with Fresnel’s drag coefficient is d = 0.2069. (Fizeau actually computed the latter as 0.2022, using the then current value of the speed of light.) Fizeau measured a fringe shift of d = 0.23, which he took as falsifying the hypothesis of complete convection, and strongly supportive of Fresnel’s coefficient (although he did not endorse Fresnel’s interpretation).

In 1886 Michelson repeated Fizeau’s experiment with several improvements to increase the accuracy of the measurement. He found that the drag coefficient, i.e., the ratio of the observed fringe shift to the shift predicted by (1), was 0.434 ± 0.02, which is consistent with the Fresnel value 1 – 1/n² = 0.437.

However, as noted by Lorentz in 1895, the simple expression 1 – 1/n² for the dragging coefficient is strictly valid only for a non-dispersive medium, i.e., a medium for which the index of refraction is independent of frequency. This is because, for any given frequency ω of incident light from the source in the lab, the relevant index of refraction is not n(ω) but rather n(ω′), where ω′ is the frequency of the light in the rest frame of the water. Since the water is moving with the speed u relative to the lab, and since the speed of light in the water is (to the first order) c/n, the Doppler effect gives us (to the first order) the two relations

Note that the relevant speed in the denominator is the speed of light in the water because, as Lorentz said, “if ω is the frequency of the source of light, the frequency at a fixed point in one of the tubes will also be ω, because the successive waves take equal times to reach this point”. (This is because the location of the column of water is stationary, even though the water itself is moving.) We then apply the usual first-order Doppler factor for a wave of speed c/n in that column to convert to the frequency at a particle moving with speed u. The minus sign applies to the light moving in the same direction as the water (so it is red-shifted in terms of the rest frame of the water), and the plus sign applies to the light moving in the opposite direction (so it is blue-shifted). Also, for a sufficiently small shift, such that the relation between n and ω is linear, we can write

Combining these two relations, we get

Thus we have

where

Note that the signs are reversed when expanding the denominator, so the plus sign gives the value of c/n(ω′) for the light moving in the same direction as the water, and the minus sign gives the value for the light moving in the opposite direction. Making these substitutions into the expression for the time difference (again using the relativistic speed composition) we find that, to the first order in u/c, the time difference is

Hence the fringe shift for a dispersive medium should be

Noting that ω = c/λ, we have dω = –(c/λ²)dλ, and so the fringe shift can be written as

For the wavelength of light used by Fizeau and Michelson, we have dn/dλ = –(0.0400)10⁶ m^–1, and so the convection coefficient in (3) is 0.4530, which is still within the experimental error of Michelson’s result. In 1915 Zeeman repeated Fizeau’s experiment with various wavelengths of light, and found the results tabulated below.

                          Wave       Eq (3)                                No. of

                           length     Predict       Measured        Trials

                           4500       0.825      0.826 ± 0.007        6

                           4580       0.808      0.808 ± 0.005        6

                           5461       0.660      0.656 ± 0.005        9

                           6440       0.551      0.542                     1

                           6870       0.513      0.511 ± 0.007        10

More recently, using modern laser optics, it has been possible to confirm the predicted drag coefficient to an accuracy of ±0.00028. (See, for example, Sanders and Ezekiel, 1988.)

Incidentally, determining the relevant value of velocity u of water in tube is not entirely trivial, because the flow is turbulent and has a velocity profile that is a minimum at the wall of the tube and a maximum at the center of the tube. The light passes through the center of the tube, so the relevant value of u is really u_max. As described by Michelson, it is relatively straightforward to determine the average speed u_ave of the water by first determining the flow rate from measuring how long it take to pass a certain volume of water, and dividing this by the cross-sectional area of the tube. Michelson then inserted pressure sensors (Pitot tubes) into the flow and, by varying the flow, determined that the pressure was proportional to the square root of the speed. He then varied the radial position of the pressure sensor and inferred that the water speed u(r) at any radial distance r from the axis (of a tube of radius R) was given closely by

where α = 0.165. Therefore the average speed is

and hence u_max = (1+α)u_ave = 1.165 u_ave.

As an aside, we note that κu is the difference between the phase velocity and the group velocity in a dispersive medium, a fact that has sometimes misled people into thinking the dispersion term in the drag coefficient is due to the replacement of the phase velocity with the group velocity. However, this is not correct, because the relevant velocity for evaluating the fringe shift is the phase velocity. Also, notice that the term involving κ is added to the phase velocity for one direction and subtracted for the other direction. It actually represents the discrete shift in refractive index due to the Doppler frequency shift, and the expression is valid only for small velocities such that the relation between n and ω is linear.

Return to MathPages Main Menu