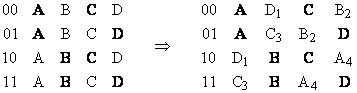Octacubic Coherence and Symmetry Breaking

When he raiseth up himself, the mighty are afraid: by reason of breakings they purify themselves.

                                                                                Job 41:25

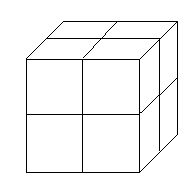
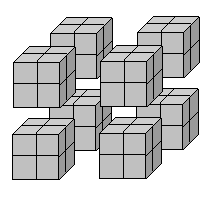
Consider a set of eight cubical blocks, arranged in the shape of a 2x2x2 “octacube” as illustrated below.

For each of the individual blocks, we label the six faces with the six letters A, B, C, D, E, and F, in some order. Question: Is it possible to label the faces and arrange the blocks into an “octacube” as shown above, such that on each face of the octacube the four blocks have the same label, and such that the faces of the blocks that touch each other have the same labels? If so, in how many distinct ways (up to rotations and permutations of the labels) can this be done?

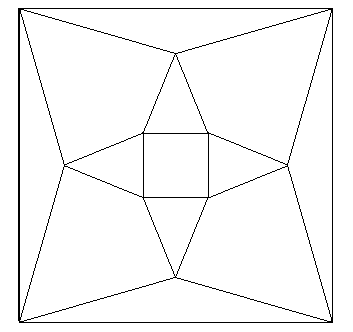
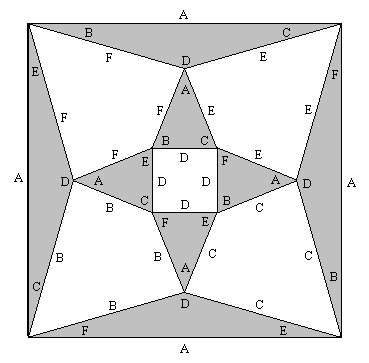
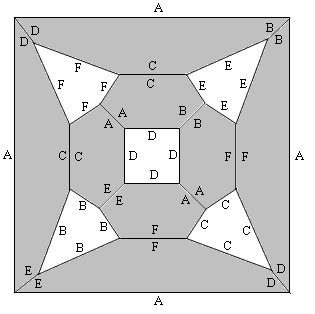
To answer these questions, notice that we can represent the topology of an octacube by the diagram shown below.

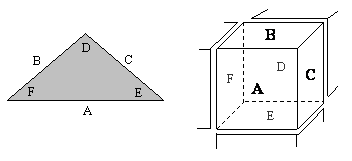
Each triangle represents one of the blocks comprising the octacube, and we identify the three external edges of the triangle with the three external faces of the block. Also, the three internal corners of the triangle correspond to the internal faces of the block. We stipulate that opposite faces of the block are represented by an external edge and the opposite internal corner of the corresponding triangle. These correspondences are illustrated in the figure below.

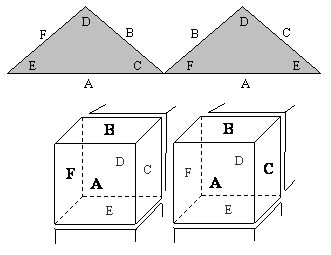
In the topological diagram, two triangles that meet at a vertex correspond to two adjoining blocks, and the faces that meet are identified with the interior corners of the respective triangles joined at the vertex. This is illustrated in the figure below for two identical adjacent blocks on the upper front row of an octacube. The blocks are shown with some separation for clarity, but face C of the left hand block is to be in contact with face F of the right hand block.

In the triangular representation, the contacting faces (C in the left block and F in the right block) are the interior corners at the joining vertex. Also, the adjoining external edges both appear on the same face of the octacube. In this example, these two blocks contribute two “A” labels on the front face, and two “B” labels on the upper face. In a completed octacube each block adjoins three others, so the eight triangles are connected to other triangles at each vertex. This leads to the topological pattern shown above. The quadrilateral regions (including the infinite region outside the circumscribing square) correspond to the six faces of the octacube.

Obviously eight blocks with the identical pattern of labels can be assembled into an octacube with coherent labels on the six external faces of the octacube, as indicated below.

Every solution must have this pattern of external labels (up to permutations of the labels), so we can take those as fixed, and proceed to determine whether it’s possible to arrange the internal labels to meet the required condition, i.e., such that all sides that touch each other have the same label. Clearly the labeling pattern shown above does not satisfy this internal requirement. For example, the upper corner of the bottom triangle is labeled D, and the lower corner of the adjoining triangle at that vertex is labeled A, so these do not match. Moreover, we can see that, in a valid solution, those two internal corners cannot possibly be assigned either A or D, because they are opposite the external edges A and D of their respective blocks. Thus we recognize that, in a valid solution, no block can have opposite face pairs that match any of the opposite face pairs of the overall octacube. In other words, since the opposite face pairs of the overall octacube are A-D, B-E, and C-F, it follows that none of the individual blocks can have any of those three opposite face pairs.

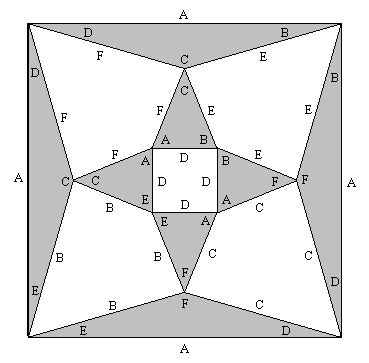
Consequently we must re-arrange the internal labels in the above diagram such that none of the labels remains in the position shown above (because, by construction, all of the opposite face pairs of each block are the forbidden pairs). Now, there are only two ways of re-assigning a set of three cyclic elements such that none of the elements remains in its original position. These re-assignments correspond to rotating the elements (by one step) either clockwise or counter-clockwise. We will find that, once we choose a rotation direction for the internal labels of one of the triangles, this fully determines the required rotation directions for all the other triangles in order to make the touching faces match.

Suppose we rotate the internal corner labels of the bottom triangle in the clockwise direction. In that case the upper internal corner of that triangle will be labeled F. We want this to be the same label as the internal corner of the adjoining triangle, so we must rotate the internal edges of that triangle in the counter-clockwise direction. By the complete symmetry of the overall construction (which has no degrees of freedom for any given valid arrangement of external labels), and confirmed by inspection, it follows that rotating in opposite directions the internal edges of any two triangles joined at a vertex results in matched labels for the opposite edges, and hence matched labels for the touching faces of the corresponding blocks. This pattern of clockwise and counter-clockwise rotations is self-consistent, because there are an even number (four) of joining triangles around each quadrilateral loop. The result of this set of rotations is shown below.

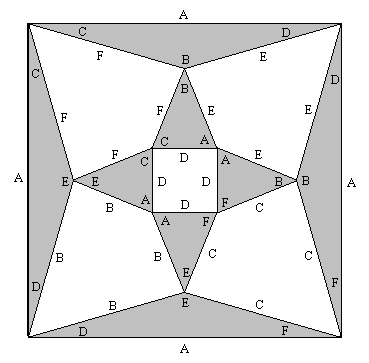
This represents a complete solution, as can be verified by inspection, noting that every pair of adjoining corners have matching labels. The only other distinct solution (up to permutations of the labels) is given by returning to the original arrangement and then rotating the internal edges in the opposite directions. (Equivalently we can simply apply one more rotation in the same directions to each triangle.) This produces the solution represented by the diagram below.

These are the only two solutions, so if we were presented with a set of eight blocks with labeled (or colored) faces and asked to assemble them into an octacube with the required properties, we know the labels (or colors) of the blocks must agree with one of these two patterns. Notice that no two of the blocks are identical in any given solution.

One might think that there are two distinct sets of blocks, each having only one possible solution, but this is not the case. The reason is that we can convert one solution into the other by turning the octacube “inside out”. Consider the bottom triangle in the above diagram of the second solution, which has the external faces A, B, C (listed in clockwise order) and the corresponding opposite internal corners E, F, D. Note that the internal corners of the triangle are listed in counter-clockwise order in the sense of a vector pointing out from their common vertex on the block. Without loss of generality, suppose this block is in the upper-front-left position, and we move it to the exact opposite position, i.e., the lower-back-right, oriented such that the edges that were internal are now external. Listing the external labels in clockwise order, the result is a triangle with external labels F, E, D and the corresponding internal labels B, A, C. This is identical to the block in the lower-back-right position of the first solution. Similarly if we swap every block of the second solution with the block in the exact opposite position, and orient them to maintain the same overall octacube labeling pattern (so all the internal block faces become external, and vice versa), we convert the second solution into the first. This shows that there is just a single unique set of block labelings, and those blocks can be assembled into either of the two solutions.

The uniqueness of the block labelings was to be expected, because it’s easy to see that there are only eight distinct labeling patterns that comply with the requirements that no label can be opposite (on a given block) the label that it opposes in the overall octacube. To see this, note that we can orient any block so the label A is on top, and then we have just four choices (B,C,E,F) for the bottom label, because it can’t be D. After choosing one of those four, say B, for the bottom label, the four remaining faces listed in order around the A-B axis must be either D(CF)E or DE(CF). The reason C and F must be adjacent is because they cannot be on opposite faces. Thus there are just 2x4 = 8 arrangements of the labels on a block. One might think we could transpose C and F, resulting in double the number of possible labelings, but these arrangements would violate the chirality (handedness) of the overall octacube. Recall that when determining the overall pattern of octacube faces, we needed to not only assign the opposing pairings AD, BE, and CF, we also needed to make a choice of chirality. Placing A and top and D on the bottom, we can rotate the octacube so B is in front and E is in back. Then the C and F faces are on the sides, but we must decide whether to put C on the left and F on the right, or vice versa. Once we’ve made this choice, the arrangements of labels on the individual blocks must conform to this chirality, which cuts the number of allowable arrangements in half, resulting in just eight possibilities. These are the eight block patterns appearing in the solutions.

If, as discussed above, we were presented with a set of eight blocks with colored faces (as with the Octa Cube puzzle by MindScope), and asked to assemble them into an octacube with the required properties, we know the colors of the blocks must satisfy all the required conditions, including the chirality condition. Based on the properties of the blocks and solutions explained above, we can assemble the blocks into one of the two solutions by the following straightforward procedure:

First examine the individual blocks to see which pairs of colors are never on opposite faces, and call these color pairs (A,D), (B,E), and (C,F). The faces of the octacube must have these opposing face pairs. Then take any of the eight blocks and position it so that three colors (e.g., A,B,C), one from each pair, are facing outward. Then place an adjacent block with the requisite colors along the exterior faces (recalling that the color of the opposite face of the octacube is known) and the contacting interior face. Proceeding in this way, piece by piece, we can completely assemble the octacube, simply by choosing the blocks with the required exterior and interior colors.

Notice that at each step of the procedure only a single block will satisfy the requirements, so there is no ambiguity. Also notice that once four blocks on one face have been positioned, we no longer need to check the interior faces, because they will automatically match. (Another approach would be to assemble the blocks without regard to the interior colors, and then at the end we can make the interior colors match by swapping one or at most two diagonally opposite pairs.) This assembly procedure gives one of the two possible solutions. To get the other solution, we would simply swap the blocks on all four main diagonals. Equivalently, we could have started by positioning the first block with the other possible orientation (noting that each block has two orientations with acceptable external face colors.)

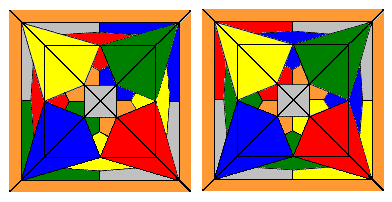
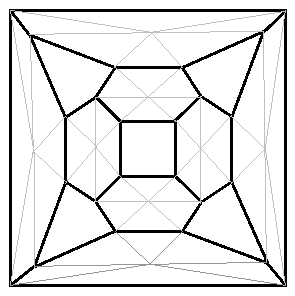
Returning to the topology diagram, we can partition the interior of each triangle into three quadrilaterals, and partition each of the main quadrilaterals into four quadrilaterals, thereby creating a tiling for each solution, consisting of 24 tiles corresponding to the six faces of the eight blocks. These colored tilings for the two octacube solutions are depicted below.

Instead of representing the blocks by triangles, we could as an equivalent alternative represent the blocks by hexagons, with each edge corresponding to a face. This is given by essentially just widening the vertices of the triangles into snub segments. With this arrangement the first solution is shown below.

If we triangulate the hexagons, so that each face of a block corresponds to one of the triangles, we get the pattern shown below.

The octacube puzzle is equivalent to asking for a coloring of the tiles of the hexagons with six distinct colors such that a single color surrounds each quadrilateral and the colors of adjacent tiles are matched. The two solutions are shown below.

This is an interesting construction, because it illustrates the concept of symmetry breaking. At the highest level we have six distinct labels (or colors) that are entirely symmetrical, but in order to associate them with the six faces of a cube we must first place the colors into pairs (of opposing faces), and then select the chirality. However, the chirality could be subsumed into the freedom to permute the colors, so this is a relatively mild form of asymmetry. We can then imagine six identical blocks, assembled to give the matching external faces, but (as discussed above) this results in mismatched internal faces. We might say, for some suitably defined “energy”, that this symmetrical arrangement of identical blocks is not a minimum energy configuration. We can reach the lowest “energy” by matching all the internal touching faces, but in order to do this we find that it’s necessary to break the symmetry (internally) of the eight blocks, and this can be done in two distinct self-consistent ways, by rotating the colors on the internal faces, in one of two counter-rotating patterns. This forces the eight originally identical blocks to be differentiated into eight distinct patterns, and the resulting assembly is intrinsically asymmetrical in the sense that it cannot be subsumed by any permutation of the colors.

Incidentally, the construction described above for coherent 2 x 2 x 2 assemblies of blocks (where “coherent” means uniform color on each external face of the overall assembly, and matching colors at every interface where two blocks touch each other) can easily be adapted to enable us to construct coherent 2^N x 2^N x 2^N assemblies. Referring to these as level-N solutions, we can begin with a Level-1 solution (as described above), and then imagine eight identical copies of this solution assembled into a 4 x 4 x 4 cube, as depicted in the figure below.

Each exterior face will have uniform color, but the interior colors won’t match. Then for each of the eight Level-1 assemblies we permute the three interior colors, either clockwise or counter-clockwise. (Notice that we cannot simply rotate the colors on the internal facing surfaces, we must permute those three colors throughout each Level-1 block, because otherwise the individual primitive blocks would not have six distinct colors, and it would upset the Level-1 solutions.) Just as for the Level-1 solution, this will leave the exterior faces unchanged, but will make all the interior faces match. Repeating this process at higher levels, we can construct arbitrarily large coherent assemblies of blocks. At each stage we have the choice of whether to permute the interior colors clockwise or counter-clockwise, so there are 2^N distinct arrangements (up to permutations) that can be formed in this way.

Another way of looking at the original construction is by constructing a table with entries for each face, and impose the coherence conditions on the labels. To illustrate, consider first the trivial 2 x 2 case, consisting of four two-dimensional squares with labeled edges, assembled so that each face of the combined assembly has uniform labels and each pair of touching faces have matching labels. As depicted below, we can proceed just as we did for the three-dimensional case, by first assembling square with identical labels, and then applying a derangement of the interior labels of each square.

Recall that in the three-dimensional case each block has three interior faces, and there are two possible derangements of three items (rotation in the clockwise or counter-clockwise direction), whereas in this two-dimensional case there is only one derangement of two items, so the solution is unique (up to permutations of the labels). To represent this in tabular form we can imagine the centers of the four squares at the Cartesian coordinates (0,0), (0,1), (1,0) and (1,1). Then for each square we can list the four one-dimensional face labels in standard order bottom, top, left, right. In this format the two arrangements above are represented by the two tables shown below.

The exterior faces of each square are shown in bold. We leave those fixed, and apply a derangement (which, in this case, is a simple transposition) to the interior faces. Considering the first two squares with the labels ADCB and ACBD we see that they share the common exterior side A, and they have the other exterior faces C and D respectively. The opposite faces of these two faces are touching, so their labels are required to match. Likewise we can determine all pairs of touching faces, whose labels must match. The four pairs of touching faces are indicated by subscripts in the right hand table.

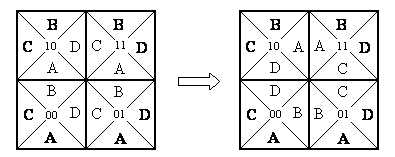
Now we can proceed, in the very same way, to construct the table representing the three-dimensional octacube arrangements. In this case there are 2³ = 8 blocks, each with 6 two-dimensional faces. We again arrange the face labels as opposing pairs in the order: front, back, bottom, top, left, right. Beginning with eight identically labeled cubes and then rotating the interior faces to the left, we get the solution shown below.

The second solution is given by rotating the interior labels once more to the left. Notice that once we select just one of the interior faces, all the rest are fully determined, so there are only two possible solutions (consistent with what we found previously). The blocks that adjoin each other are those whose coordinates differ in just one direction, and that contribute to two exterior surfaces in common. For example, 001 and 101 differ in just one direction, and they contribute to the common exterior surfaces C and F.

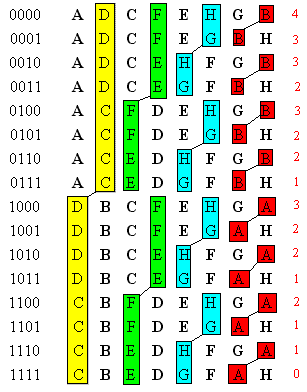
Next we consider the four-dimensional case, consisting of an assembly of 2⁴ = 16 four-dimensional “cubes”, each of which has 8 three-dimensional “faces”. The pattern of exterior surface faces is the same, shown by the bold labels, but in this case there are four interior faces for each block. There are 9 possible derangements of 4 items, and by choosing one of those and applying it to the interior labels of every block, we arrive at a solution. For example, the table below gives the solution produced by applying a leftward rotation.

The pattern of matching internal faces is the same as before, so we’ve omitted the subscripts. This pattern is depicted in the figure below.

The numbers appearing to the right of the labels signify the number of the internal labels for each block that are unconstrained by prior entries in the table.

In this case the derangement need not be a rotation. For example, applying the derangement of four items consisting of two permutations (i.e., sending 1234 to 2143) also gives a satisfactory solution. Furthermore, it isn’t even necessary to apply the same derangement to the internal faces of each block. There are solutions in which different derangements are applied to different blocks. This is unlike the two-dimensional and three-dimensional cases. Thus some additional constraints must be applied in order to reduce the number of solutions in four dimensions. Alternatively, we could define a potential energy for configurations, and seek the arrangement with the lowest energy.

Return to MathPages Main Menu