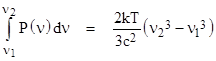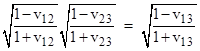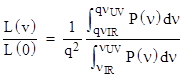Disappearing Sun

I know you all, and will awhile uphold

the unyoked humor of your idleness,

Yet herein will I imitate the Sun…

                                 William Shakespeare

If an observer (at a distance of, say, many light years) is moving at constant speed directly toward the Sun, how would the visible electromagnetic energy per unit time received by this observer (at a given location) depend on the observer’s speed?  In particular, is the Sun nearly “dark” (no energy in the visible spectrum) for an observer approaching at sufficiently high speed?

We avoid referring to acceleration in our statement of the question, because any finite acceleration would involve a passage of time and therefore a change in the distance of the object from the Sun, and the amount of change would depend on the rate of acceleration. Obviously any reduction in the spatial distance (in terms of the Sun’s rest frame) would contribute to increasing intensity of the radiation from the Sun, simply by virtue of getting closer. Also, acceleration itself would raise the issue of Unruh radiation. In addition, even for constant speed at a given instant, there would be complications related to absorption bands for the tenuous material in inter-stellar space. But in this discussion our interest is purely in the effect of constant speed at a given location, i.e., a given distance from the Sun (again, in terms of the Sun’s rest frame), assuming a perfect vacuum.

The question reduces to whether the Doppler effects, both on frequency and amplitude, applied to the low-frequency end of the Sun’s spectrum, would tend toward blackness asymptotically for sufficiently high speed. Clearly the answer depends on the spectrum of electromagnetic radiation emanating from the Sun.  If there is some positive minimum frequency (i.e., maximum wavelength) for the Sun’s emissions, then we can obviously choose a speed of approach that causes the received radiation at that minimum frequency (and hence at all frequencies of the Sun’s radiation) to be Doppler shifted up above the visible range of frequencies, making the Sun visibly black.  Needless to say, any actual observer in such a situation would be subjected to highly intense x-rays and other high frequency radiation, so for sufficiently high speed any realistic human eye would be destroyed instantly (rendering the observer incapable of seeing the Sun – or anything else), but our interest is just in the theoretical possibility of shifting arbitrarily much of the Sun’s electromagnetic radiation out of the visible range.

Now, the actual spectrum of the Sun is not a simple distribution (even setting aside any absorption issues), but over a wide range of frequencies the Sun’s spectrum is closely approximated by that of a black-body radiator, i.e., it has a power density spectrum adhering closely to the form

where P(ν) is the emitted energy per unit time, per unit area of the emitting surface, per unit solid angle, and per unit frequency. In this expression T is the temperature of the emitting surface, h is Planck’s constant, k is Boltzmann’s constant, and c is the speed of light. The energy per unit time (i.e., the power) of the radiation (per unit emitting area and solid angle) over any given range of frequencies is the integral of P(ν)dν over that range. Since we are considering two identical observers at the same distance from the source, differing only in their speeds (which doesn’t affect their transverse cross-section), it follows that the power absorbed by observers at various speeds at that location is proportional to this integral.

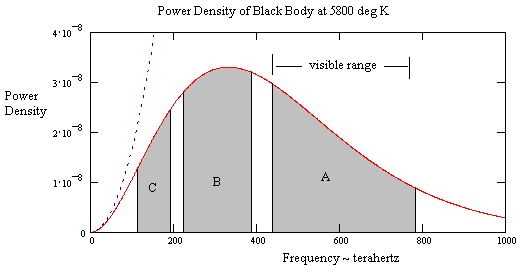
The Sun’s spectrum is quite closely approximated by a black body spectrum with a temperature of about 5800 deg K.  A plot of this spectral density is shown below.

The range of frequencies visible to the human eye extends from 430 to 790 terahertz.  (A terahertz is 10¹² cycles per second.) We note in passing that the visible range of frequencies does not encompass the peak of the Sun’s power density. The maximum density of the Sun’s spectrum is actually in the infrared region, at about 330 terahertz. This may be surprising to readers who have seen the Sun’s power density plotted as a function of wavelength instead of frequency, and noted that the visible wavelengths are at the peak of the density curve. On this basis it is sometimes claimed that the human eye is somehow tuned (perhaps by evolution) to the peak of the Sun’s power density. However, the conversion between a density function based on wavelength and a density function based on frequency alters the shape of the curve, so on a frequency basis the eye’s visible range is not at the peak. This somewhat undermines the idea that the human eye evolved to perfectly match the Sun’s spectrum.

The power in this visible range is represented by the shaded region denoted by A. The region denoted by B covers the range of visible frequencies divided by 2, so if the observer had a high speed toward the Sun such that the frequencies were all Doppler shifted by a factor of 2, this would be the light in the visible range. The integrated area (and hence the power) of region B is less than that of region A, but the Doppler shift would increase the intensity by a factor of 4, i.e., the square of the frequency ratio. Since the area of B is more than a fourth the area of A, the visible power received by an observer with that velocity would be increased.

For an observer at that same location with an even greater speed toward the Sun, such that the Doppler shift increases the frequencies by a factor of 4, represented by the region denoted by C in the above figure, we would find the visible power is still increased,  because the area of C is more than 1/16 the area of A. However, by this point the visible power is actually beginning to drop, because both the height of the shifted region and the width are decreasing, and eventually the power density of the electromagnetic rays from the Sun in the visible range would drop below the power for a resting observer. In fact, we can show that it ultimately approaches zero for ultra-relativistic speeds approaching the speed of light.

We might question whether the Sun, or any other real physical system, can emit energy down to arbitrarily small frequencies, corresponding to arbitrarily long wavelengths. Can a cavity radiate electromagnetic waves with wavelengths longer than the size of the cavity itself? Can an antenna emit waves with wavelengths longer than the length of the antenna? If there is a lower limit to the frequencies emitted by the Sun, then obviously with a sufficient speed of approach we could shift all the power up above the visible range. But suppose we assume the Sun actually does emit energy down to zero frequency, in accord with the theoretical black body spectrum. In that case, can the Sun be made to fade completely to black (or arbitrarily close to it) by a sufficiently high speed of approach?

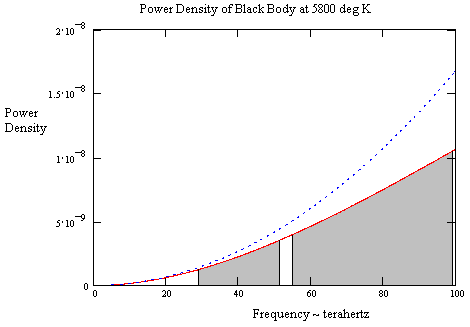
To quantitatively evaluate the asymptotic behavior at ultra-relativistic speeds, we can focus on just the very low frequency range of the spectrum (in its own rest frame). In this regime the black body spectrum can be represented by just the first term in the series expansion of the power density function, which is

A plot of the actual black body spectrum and this low-frequency asymptote (the dotted line) is shown below.

As we proceed to lower and lower frequencies the actual density approaches the asymptote. The integral of this asymptotic density from ν₁ to ν₂ is

The power incident on an observer moving with a certain relativistic speed toward the Sun would be of this form, and we can then consider a second observer moving with speed v toward the Sun relative to the first observer. The light visible to this second observer will be Doppler-shifted up from a range of frequencies lower than that of the first observer by a Doppler shift factor

It follows that, in the Sun’s frame, the incident power on the second observer in the range visible to that observer is given by the same expression as above, except ν₁ and ν₂ are replaced with qν₁ and qν₂. Consequently, for sufficiently low frequencies, the ratio of incident powers in the respective visible ranges is simply q³. However, in terms of the frame of the second observer, the intensity of the light Doppler-shifted up to a higher energy in proportion to the square of the reciprocal Doppler factor, which provides a factor of 1/q². Therefore, the asymptotic ratio of the powers incident on the second observer to the power incident on the first observer, given that the second is moving with speed v relative to the first, is simply q. It follows that the asymptotic ratio has the form Cq for some constant C. (See below for the determination of this constant.)

Note that this is consistent with the relativistic composition of speeds, since if we consider three different observers at this location, and the second observer is moving toward the Sun with speed v₁₂ in terms of the rest frame of the first, and the third observer is moving with speed v₂₃ in terms of the rest frame of the second, then according to our preceding derivation the ratio of the visible power of the third observer to that of the first must be the product of the squared Doppler factors for speeds v₁₂ and v₂₃, but it must also equal the squared Doppler factor for the single speed v₁₃ of the third observer in terms of the rest frame of the first. Thus we must have

Squaring both sides and solving this for v₁₃ gives

which of course is the relativistic composition law for speeds.

Returning to the exact black body density distribution, and letting L(v) denote the rate of energy in the visible range impinging on a given object at a given location moving with speed v toward the Sun, we can apply the same reasoning as above to express the exact ratio of L(v) to L(0) by evaluating the expression

where ν_IF and ν_UV denote the infrared and ultraviolet frequency limits of visible light. A plot of this function is shown below.

Thus even if the Sun emits energy at all frequencies down to zero in accord with the theoretical blackbody spectrum, the incident visible power could (in principle) be made arbitrarily close to zero for a sufficiently high speed of approach. The power is increased for speeds up to about 0.825 times the speed of light, but beyond that the power begins to drop, and goes to zero for speeds approaching the speed of light.

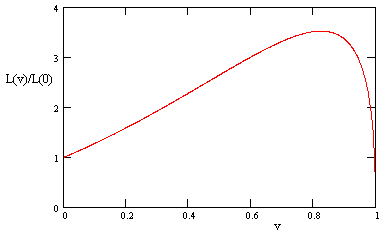
To show that this is consistent with the asymptotic behavior derived previously, we can plot the ratio of the visible power received by an observer moving toward the Sun with speed v relative to an observer moving toward the Sun with the speed v in terms of the Sun’s rest frame. By the relativistic composition of speeds, this implies that the first observer has speed 2v/(1+v²) in terms of the Sun’s rest frame. A plot of this ratio, along with the asymptotic ratio (1-v)/(1+v) derived previously, is shown below.

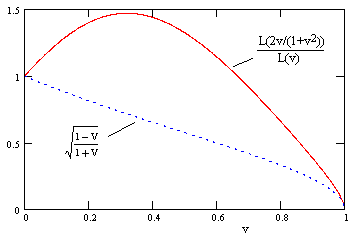
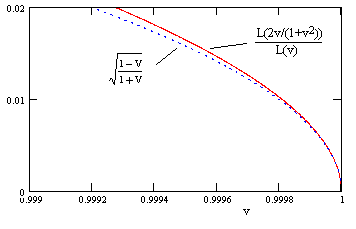
Focusing on the extreme high speed end, we see that these two functions are indeed asymptotic to each other, as shown below.

To express these results in terms of magnitude, as defined by astronomers, recall that this tradition dates back to Hipparchus, who classified the visible stars into six “magnitudes”, with the first magnitude being the brightest and the sixth being the dimmest. The magnitudes were spaced uniformly according to the perceived sense of brightness, although it was later realized that each of these steps (from one magnitude to the next) represented a factor of about 2.512 in the intensity of the electromagnetic wave.  Hence, like most human senses, it is essentially logarithmic. In modern astronomy two stars are said to differ by one magnitude if the ratio of their intensities (over the whole spectrum) is 2.512. Therefore, the magnitude shift for a speed v relative to the brightness in the rest frame of the star is the value of m such that L(v)/L(0) equals 2.512^m. Taking the natural log of both sides, this implies

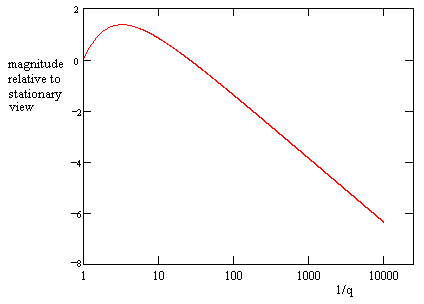
A plot of the magnitude (relative to the stationary brightness) versus the reciprocal Doppler factor 1/q is shown below.

For example, to achieve a six magnitude reduction in the visibility, this shows that we need a reciprocal Doppler factor of 1/q = 7161, corresponding to a speed of v = 0.999999961 toward the Sun.

Incidentally, we can simplify the equations by considering just a thin slice of the visible spectrum and showing how the intensity in just that slice is affected by speed, since all the slices are affected in similar proportions. To represent a uniform weighting of the eye’s sensitivity over the visible range of frequencies (as we’ve assumed above) the optimum single frequency is 584 terahertz, near the middle of the visible spectrum. Letting ν₀ denote this frequency, the expression for L(v)/L(0) reduces to

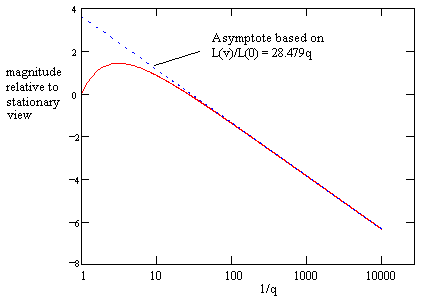
A plot of this function is indistinguishable from the plot of the actual function (found by integrating the full spectrum) shown above. Moreover, expanding this to a series in q and taking the first term, we find that for small q the intensity ratio is asymptotic to

confirming our original assessment of the asymptotic behavior (and determining the value of the constant C discussed above). A plot of this asymptote is shown in the figure below.

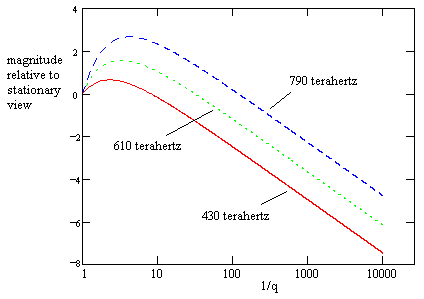
More generally we can plot the effect of speed on the visible magnitude for several individual frequencies covering the visible range, as shown below.

To account for the fact that the human eye is more sensitive to frequencies near the middle of the visible spectrum, we could set ν₀ = 610 terahertz, the mid-point of the visible spectrum. Indeed the middle line in the above plot provides a good representation of the overall perceived brightness (as can be confirmed by integrating over the range of frequencies with a normally distributed sensitivity profile). On this basis, to achieve a six magnitude reduction in the visibility, we need a reciprocal Doppler factor of 1/q = 8680, corresponding to a speed of v = 0.999999973 toward the Sun. Comparing this with the previous result based on uniform sensitivity shows how much the precise answer depends on what we take to be the detailed spectral sensitivity of the human eye.

We should mention that, at such ultra-relativistic speeds, aberration would cause the apparent positions of all the surrounding stars to shift forward and cluster toward the point directly ahead of the observer, so there would be a concentration of all the incoming radiation from all external sources into a small angular arc directly ahead. What we’ve been considering here is just the light from one particular star, such as the Sun, showing that the power in the visible range from such a star approaches zero in the limit as the speed approaches the speed of light. Of course, just because the energy arriving from the Sun has been pushed up out of the visible range, it would be far from inconspicuous. The intensity of the x-rays and higher frequency radiation when approaching the Sun at such ultra-relativistic speeds would increase without limit, and at sufficiently high speeds would be intense enough to incinerate our eyes.

Return to MathPages Main Menu