|
Kinematics and Dynamics in Special Relativity |
|
|
|
The description of right lines and circles, upon which geometry is founded, belongs to mechanics. Geometry does not teach us to draw these lines, but requires them to be drawn. |
|
Isaac Newton |
|
|
|
I am coming more and more to the conviction that the necessity of our geometry cannot be demonstrated...geometry should be ranked, not with arithmetic, which is purely aprioristic, but with mechanics. |
|
Carl Gauss |
|
|
|
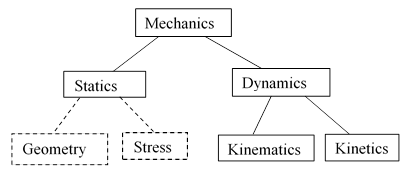
According to the traditional definitions, kinematics is one of the two branches of dynamics, the other being kinetics. The book “Statics and Dynamics” by Beer & Johnston gives typical definitions for these terms: |
|
|
|
Dynamics is divided into two parts: (1) Kinematics, which is the study of the geometry of motion; kinematics is used to relate displacement, velocity, acceleration, and time, without reference to the cause of the motion. (2) Kinetics, which is the study of the relation existing between the forces acting on a body, the mass of the body, and the motion of the body; kinetics is used to predict the motion caused by given forces or to determine the forces required to produce a given motion. |
|
|
|
This is consistent with the definitions of kinematics and kinetics given in the article on mechanics in the 1969 edition of Encyclopedia Britannica, where the entire subject of mechanics (including statics) is categorized as shown schematically below: |
|
|
|
|
|
|
|
We’ve included the subjects of geometry and stress under the heading of statics, by analogy to the sub-categories of kinematics (the geometry of motion) and kinetics (consideration of forces) under dynamics. The two epigraphs above, quoting Newton and Gauss, show that the placement of geometry within mechanics is not a new idea. (Of course, this refers to geometry as a representation of the spatial relations of our experience, not geometry as an abstract axiomatic structure.) But this makes the distinction between geometry and stress problematic, because any metrical features of geometry must be founded operationally on physical entities or processes that enable measurement, and this includes equilibrium configurations of “solid” objects whose solidity depends on a balance of stresses. Hence it is questionable whether the subjects of geometry (in the physical sense) and stress can be properly separated. This is what prompted Poincare to remark that “If there were no solid bodies in nature, there would be no geometry”. The distinction between kinematics and kinetics is even more problematic, because it entails the coordination of temporal as well as spatial measures, which ultimately depends on the kinetic (inertial) behavior of physical entities. In a pre-relativistic context, with the (incorrect) assumption of the possible existence of accelerating “rigid” bodies, the implicit reliance of kinematics upon kinetics is easily overlooked, and in that (counter-factual) context the distinction between those two concepts could be rationalized to some extent. Thus Greenwoods’s “Principles of Dynamics” says |
|
|
|
Kinematics is the study of the motions of particles and rigid bodies, disregarding the forces associated with those motions. It is purely mathematical in nature and does not involve any physical laws such as Newton’s laws. |
|
|
|
But this kind of distinction is nominally viable only in Galilean relativity, and, even then, only by neglecting the operational (kinetic) basis of our measurements. In the context of special relativity that basis becomes impossible to neglect. Hence special relativity reveals that the distinction between kinematics and kinetics is (and always was) untenable. We could paraphrase Poincare and say “If there were no such thing as inertia and the persistent existence of identifiable physical objects through time, there would be no kinematics”. |
|
|
|
In the context of special relativity one often sees the word “kinematic” used to characterize certain physical facts – such as the increased inertia of moving objects, i.e., the increased force required to accelerate a moving object due to the inertia of energy. If we apply the standard definitions of the word “kinematic” noted above, such characterizations are self-evidently false, because kinetics (in contra-distinction to kinematics) refers explicitly to “the forces required to produce a given motion”. Hence it’s clear that, when people say the effects of special relativity are “kinematic”, they are either mistaken or they are using the word in a different sense than its actual formal definition within the field of mechanics. Adding to the confusion, people also tend to contrast what they call “kinematics” with what they call “dynamics”, which makes no sense according to the formal definitions of those words, because kinematics is actually part of dynamics. Philosophers of science seem to sometimes use the word “dynamics” to refer to what is properly called “kinetics”. Unfortunately this semantic confusion is so deeply embedded in the literature that it’s impossible at this stage to eliminate it. In the following discussion we will sometimes just acquiesce in using the word “dynamics” to refer to what would properly be called kinetics. |
|
|
|
The notion that the propositions of special relativity are kinematic may be traced back to Einstein’s original paper of 1905 on the electrodynamics of moving bodies. The first part of the paper is labeled “Kinematic Part” (Kinematischer Teil), and yet the very first sentence is |
|
|
|
Let us take a system of co-ordinates in which the equations of Newtonian mechanics hold good. |
|
|
|
Thus he begins by specifying a system of inertial coordinates on the basis of Newton’s dynamical laws, and the paper’s subsequent discussion consists entirely of statements that are true only on the basis of those dynamically (kinetically) defined inertial coordinates, so the entire discussion is based squarely on dynamics (kinetics). Of course, as we’ve discussed elsewhere, there are some difficulties with Einstein’s statement. For example, the remainder of the paper explains that the equations of Newtonian mechanics actually do not hold good in terms of any system of coordinates. Hence one might think the above quoted sentence was simply erroneous. However, in later re-publications a footnote was added, saying “i.e., to the first approximation”. Reportedly this footnote was added by Sommerfeld when he edited a collection of relativity papers for a book published by Meuthen in 1923. (Einstein never voiced any objection to the addition of this footnote.) With this clarification, the sentence signifies that we are to consider a system of coordinates in terms of which the equations of Newtonian mechanics – with no fictitious force terms - are at least quasi-statically valid. It’s important to note that the sentence refers to equations (plural), not just to Newton’s first law. The system of coordinates must be such that all three of Newton’s laws are quasi-statically valid. This suffices to fully determine a system of space and time coordinates (up to scale factors determined by considerations of internal energy), including the unique synchronization of the time coordinate at spatially separate locations necessary for Newton’s third law to be satisfied. For any frame we synchronize clocks using two identical particles initially adjacent and at rest in the frame, and exerting mutual repulsive force on each other (expending a standard amount of energy), stipulating that they reach equal distances in equal times. This suffices even in the quasi-static limit. |
|
|
|
Occasionally people suggest that, instead of Sommerfeld’s clarifying remark, Einstein should simply have referred to coordinates in which the equations of Newtonian mechanics were thought to hold good. This would avoid the contradiction with the remainder of the paper – but it would also render the sentence meaningless. The purpose of the sentence is to specify an operational definition of a suitable system of coordinates, and this is accomplished (as noted above) by stipulating that the equations of Newtonian mechanics are quasi-statically valid in terms of those coordinates. If Einstein had simply asked us to consider coordinates in which those equations were thought to (but didn’t actually) hold good, then we would be left with no meaningful specification of the coordinates. Hence Sommerfeld’s footnote is the correct and essential clarification. |
|
|
|
Unfortunately, the remainder of Einstein’s 1905 paper never clearly articulates the fact that Newton’s (quasi-static) laws suffice to fully determine the inertial measures of space and time, including a unique simultaneity for each frame. In fact, when he subsequently describes a method of synchronizing the time coordinate of a given frame by stipulating that the speed of light is isotropic, he neglects to mention that this yields the very same synchronization given by stipulating that mechanical inertia is (quasi-statically) isotropic in Newtonian mechanics. Instead, he emphasizes the freedom of choice in selecting a synchronization procedure, obscuring the crucial identity between the coordinate systems based on isotropy of the speed of electromagnetic waves and coordinate systems based on isotropy of mechanical inertia. This identity expresses the very essence of special relativity, i.e., the fact that all forms of energy have inertia, and hence every system of measure based on the stipulation of isotropic (and homogeneous) inertia will naturally yield the same measures. |
|
|
|
So, we’ve seen that the “kinematical part” of Einstein’s paper was actually based entirely on dynamics (i.e., kinetics), and hence it was not kinematical at all, at least according to the traditional definition of that word from the field of mechanics. (We assume the German word “Kinematischer” had the same definition as the English word “kinematical”.) Thus, without completely re-defining the word “kinematics”, it is surely incorrect to say that the relativistic dependence of inertia on speed is a purely kinematic fact. Any mention of inertia automatically places it outside the realm of kinematics according to the traditional meaning of the word, so anyone who says this effect is purely kinematic must be using the word with a different meaning. |
|
|
|
Sure enough, we can confirm this by examining several modern discussions. For example, in his biography of Einstein, Abraham Pais commented on the dependence of inertia on speed as follows |
|
|
|
Long before it was known that the equivalence of energy and inertial mass is a necessary consequence of the relativity postulates and that this equivalence applies to all forms of energy, long before it was known that the separate conservation laws of energy and of mass merge into one, there was a time when dynamic rather than kinematic arguments led to the notion of electromagnetic mass, a form of energy arising specifically in the case of a charged particle coupled to its own electromagnetic field… Special relativity killed the classical dream of using the energy-momentum-velocity relations of a particle as a means of probing the dynamic origins of its mass. The relations are purely kinematic. |
|
|
|
This would be self-contradictory if Pais were using the word “kinematic” in the traditional sense, because the inertia of energy is dynamical (kinetic) by definition. Nonetheless, it is undeniable that special relativity represented an important shift in our point of view; the question is whether the word “kinematics” accurately captures the nature of this new point of view for the relativistic relations. Pais prefaces his comment about kinematics by noting that in special relativity “the equivalence of energy and inertial mass… applies to all forms of energy, [and] the separate conservation laws of energy and of mass merge into one”. True enough, but this is no grounds for referring to the relations of special relativity as purely “kinematic”. In fact, to the contrary, it implies that there are no purely kinematic relations that can be separated from dynamics (kinetics), just as there are no rigid bodies. Recall that Greenwood’s definition said kinematics concerns the motions of rigid bodies – which of course do not even exist in special relativity. Likewise, although accelerating frames are on an equal footing with inertial frames according to kinematics, such frames do not even exist in special relativity, because Born-rigid motion can only extend over a finite region. More fundamentally, as soon as we distinguish between the time coordinates of two different inertial coordinate systems, or between proper time and coordinate time, we can no longer claim to be dealing with purely kinematical relations. (Even with a geometrical interpretation of the invariant intervals, geometry must still be founded in mechanics, as Newton, Gauss, and Poincare mentioned.) |
|
|
|
To understand the distinction that Pais was evidently trying to make, it’s worth reviewing the historical investigations into how the mass of a particle depends on its state of motion. Around the turn of the 20th century it was known that the resistance to acceleration of a charged particle is at least partly due to self-inductance, and hence as the particle’s speed increases, so too does its “electro-magnetic mass”. On the other hand, it was presumed (by many scientists) that the resistance to acceleration of a mechanical mass was invariant, as Newton believed. If this were true, then by examining the resistance to acceleration of charged particles at various speeds, it would be possible to determine how much of the particle’s resistance to inertia was due to self-induction (electromagnetic mass), and how much was just mechanical mass. The experiments revealed that all of the particle’s mass is affected by speed in exactly the same proportion. At first this was interpreted to mean that all of the electron’s mass is electro-magnetic in origin. However, special relativity undermined this conclusion, because, as Pais rightly noted, it implies that all energy (including kinetic energy) has inertia, so the laws of conservation of energy and mass merge into one, and hence we will see the same relativistic dependence of inertia on speed, regardless of the form of the mass-energy. This is why Pais says that “special relativity killed the classical dream of using the energy-momentum-velocity relations of a particle as a means of probing the dynamic origins of its mass.” That is perfectly true, except for the ambiguity of the word “dynamic”. But this does not warrant the concluding sentence: “The relations are purely kinematic.” He should have said “All the relations are equally dynamical (or rather, kinetic).” Notice that we refer to the inertia of kinetic energy, not to the inertia of “kinematic energy”. The latter would be a contradiction in terms. |
|
|
|
We find a discussion of this same subject in a note by Michael Janssen, who also uses the word “kinematical” to characterize special relativity’s treatment of various phenomena. Fortunately, he helpfully explains what he actually means by that word: |
|
|
|
What it means for a phenomenon to be kinematical, in the sense in which I want to use this term, is that it is nothing but a specific instance of some generic feature of the world, in the case of the phenomena examined in this paper instances of default spatio-temporal behavior. |
|
|
|
This definition of the word “kinematical” is quite different from the traditional definitions that we’ve seen from the field of mechanics. Notice that Janssen’s “default behavior” cannot be referring to force-free behavior, because the only non-trivial relations in special relativity involve changes and interactions, such as the increased inertia (response to forces) of high speed objects. He clearly has in mind something like Pais’s understanding that all mass-energy possesses inertia, from which it follows that the “default” inertial behavior of objects in response to applied forces does not and cannot distinguish between different forms of mass-energy. The principles of special relativity imply that the speed of propagation of electromagnetic waves is isotropic in terms of the very same class of coordinate systems in which mechanical inertia is isotropic. In view of this, attempts to distinguish Lorentz invariant mass-energy from any putative non-Lorentz invariant mass-energy are doomed to failure (because the latter does not exist), just as are attempts to detect a locally distinguished frame of reference (measuring the ether wind) by comparing electromagnetic and mechanical aspects of a physical system. According to the Einsteinian interpretation, all mass-energy (including kinetic energy) has inertia and all forces are Lorentz covariant, and these postulated facts are encoded into the postulated structure of spacetime. |
|
|
|
Janssen’s comment appeared in a paper where he argues against claims of those who contend that a Lorentzian view of relativity provides a “dynamical” (and hence more meaningful or useful) explanation for relativistic relations. This neo-Lorentzian view (although the proponents deny being neo-Lorentzians) is clearly misguided, and Janssen is right to refute it. Claiming to have a dynamical (kinetic) explanation for special relativity is like claiming to have a dynamical explanation for the conservation of energy or momentum. These basic principles serve as the foundation of dynamics, so it would be circular to try to “explain” those principles dynamically. They could only be explained by some still more fundamental principle – which itself would then presumably stand in need of explanation. Lorentz recognized (albeit somewhat grudgingly) the merit of Einstein’s interpretation when he said |
|
|
|
[Einstein] may certainly take credit for making us see in the negative result of experiments like those of Michelson, Rayleigh and Brace, not a fortuitous compensation of opposing effects, but the manifestation of a general and fundamental principle. |
|
|
|
However, having said all this, it doesn’t follow that the relations arising from the principle of special relativity are purely “kinematical” (in the traditional meaning), any more than the relations arising from the conservation of energy-momentum are purely kinematical. They are indeed (in Janssen’s words) generic features of the world, but that is not the meaning of the word “kinematic”, unless (like Janssen) we simply re-define the word so that it means “a generic feature of the world”. Later in the same paper he writes |
|
|
|
According to special relativity the velocity dependence of mass has nothing to do with the specifics of the dynamics of electromagnetism, ether pressure, or what have you, but is a generic property of closed systems in a world in accordance with the postulates of the theory. The velocity dependence of mass is thus kinematical in the broad sense of being independent of the details of the dynamics. I shall argue below that this is because it is also kinematical in the narrow sense of exemplifying default spatio-temporal behavior. |
|
|
|
It’s important to remember that Janssen is not using the word kinematical in the sense of its traditional definition within mechanics. He has given the word a new definition. There is really no justification for associating the concepts he is describing with the word “kinematical” in its original definition. In fact, the definitions that Janssen gives are directly contrary to the traditional definition of the word – which makes the usage rather unfortunate, even though (as we’ve seen) this usage has an intimidating pedigree. Properly speaking, the word “kinematics” is a sub-category of dynamics, consisting of the part of dynamics that excludes kinetics. If something involves kinetic aspects of dynamics, it cannot properly be called purely kinematic. For example, the conservation of momentum for any physical system is “independent of the details of the dynamics”, so according to Janssen’s definition, the conservation of momentum would have to be called a purely “kinematical” fact, and yet no one would say the conservation of momentum is a purely kinematic aspect of mechanics, because it is the very definition of dynamics (kinetics). Likewise Janssen’s category of “kinematical in the narrow sense”, involving his concept of “default spatio-temporal behavior” does not correspond to anything in the traditional definition of the word “kinematical”. (I would also argue that his “broad sense” and his “narrow sense” are the same, since he is basically just replacing “generic” with “default”.) |
|
|
|
On the other side of the argument, the neo-Lorentzians are misusing the word “dynamical” (by which they presumably mean what was traditionally called “kinetical”). When they say “dynamical” they really mean something like “contingent coincidences”. Recall that, according to the neo-Lorentzian view, relativity is not to be seen as a generic feature of the world, it is a collection of contingent facts, e.g., electromagnetism appears (so far) to be Lorentz covariant, and mechanical inertia appears (so far) to be Lorentz covariant, and the strong nuclear force appears (so far) to be Lorentz covariant, and so on. Each of these is viewed as an independent and contingent fact, and we are urged to seek new phenomena that might violate Lorentz covariance. Indeed this was the view of Lorentz himself, who argued that when studying any new physical phenomenon we should not just assume from the start that it will be Lorentz invariant. Deep down, he expected Lorentz invariance to fail at some point, vindicating his conception of an absolute rest frame (which he admitted in private correspondence with Einstein was based partly on his spiritual views). |
|
|
|
For this reason, some modern dissidents claim that (for example) faster-than-light travel is possible under the Lorentzian interpretation of special relativity, since the “contingent coincidence” interpretation only rules out violations of Lorentz invariance for phenomena we already know about, not necessarily for yet-to-be-discovered phenomena. Of course, their anticipated faster-than-light travel would be in prospect only if Lorentz invariance fails at some point. If, for example, a fifth force was discovered, and it was found to propagate much faster than light, it would single out a distinguished rest frame, and this violation of Lorentz invariance would falsify the Einsteinian interpretation of special relativity as “a generic feature of the world”. In contrast, the neo-Lorentzians could just add it to their catalogue of contingent facts, since they are not committed to Lorentz invariance as a generic feature of the world. Oddly enough, neo-Lorentzians seem to regard this flexibility as a virtue, but in fact it is a weakness. The fewer constraints a theory places on the facts, and the less falsifiable it is, the weaker it is. Special relativity places very strict and inflexible constraints on the form of all physical phenomena, which means it is perpetually exposed to falsification in many ways. This is why it is a much stronger and more useful interpretation – as long as it remains un-falsified. |
|
|
|
A good example of the strength and heuristic value of the Einsteinian interpretation is the development of quantum field theory. Recall that Schrodinger’s equation for ordinary quantum mechanics is not Lorentz invariant, although it is quite successful in accounting for a wide range of phenomena. A neo-Lorentzian would be perfectly happy with this state of affairs – in fact, he would be ecstatic, since it seems to vindicate his faith that nature is not really perfectly Lorentz invariant. He might labor for years or decades trying to devise ways of “measuring the ether wind” by exploiting the non-Lorentz invariance of the Schrodinger equation. However, Dirac was a relativist, i.e., he regarded Lorentz invariance as a generic feature of the world, and hence believed that the correct equation simply must be Lorentz invariant. By a remarkable feat of audacious mathematical reasoning he succeeded in discovering a relativistic equation (called the Dirac equation) for an electron, which laid the foundation for quantum field theory, arguably the most successful physical theory ever conceived. Without being motivated by the conviction that there must be a Lorentz invariant quantum equation for the electron, it is difficult to imagine anyone ever developing the Dirac equation. |
|
|
|
Of course, one could cite general relativity as another example of an incredibly successful theory that owes its existence in large part to the belief that (local) Lorentz invariance is a “generic feature of the world”, rather than just a property that happens to be satisfied (coincidentally) by all phenomena we know so far. |
|
|
|
When people claim that the impossibility of accelerating a massive object to the speed c is purely kinematic, they sometimes argue that this follows from the relativistic rule for velocity compositions – which they contend is purely kinematic. Consider for example a sequence of particles on a line, each moving with a specific speed v in terms of the rest frame of the preceding particle. Using the composition rule, every particle’s speed will be less than c relative to the rest frame of the first particle. But of course this is not purely kinematic, because the relativistic formula for the composition of speeds refers to speeds defined not in terms of arbitrary coordinates, but only in terms of inertial coordinate systems, and such systems are defined kinetically, so they are outside the realm of kinematics. This applies to Newtonian mechanics just as much as it does to special relativity, although it is obscured in many introductory presentations by smuggling in an intuitive notion of an inertial coordinate system (reference frame) at the start, without any satisfactory operational definition, and then presenting the “laws of motion” in terms of such coordinates. Only later does the student realize that the inertial coordinate systems are essentially defined by those laws. For example, as noted above, two identical particles initially adjacent and at rest in a given frame, and exerting mutual repulsive forces on each other, will reach equal distances in equal times. This proposition is called the "law" of action and re-action, and represents the conservation of momentum... but of course it is not true unless we define our system of space and time coordinates to make it true, by stipulating the unique synchronization of the time coordinates at spatially separate locations such that the equations of Newtonian mechanics hold good (quasi-statically). This, or something equivalent to it (such as using light signals), is the only real basis for establishing inertial coordinate systems. |
|
|
|
It may seem surprising that the laws of motion are valid only in terms of coordinate systems defined as the coordinates in terms of which those laws are valid. This may give the impression that the laws are tautological and devoid of physical meaning, but it actually just illustrates the fact that the epistemological basis of physical theories is more subtle than it may appear. Our measures of space and time are indeed based on the very phenomena that the laws of motion are intended to describe. The "discovery of the laws of motion" consisted of people like Galileo and Newton noticing that it is possible to assign space and time coordinates to events in such a way that physical phenomena obey a simple set of mathematical equations, which they called “laws”. Thus the laws and the coordinate systems in which they are true were part of the same discovery. These seemingly tautological assertions/definitions derive their significance from the empirical fact that, once we've defined a system of coordinates in which the given property is satisfied for one pair of particles, we find that it is satisfied for all pairs of particles. In this way, what began as a definition ends as an empirical law. (As Newton said, the whole burden of philosophy is to infer patterns from phenomena, and then using those patterns to predict other phenomena.) Beginning students of special relativity often complain that defining simultaneity as whatever it needs to be to make light speed isotropic implies that the isotropy of light speed is purely tautological, but, again, the utility of the definition is that it correlates a wide range of conceivably independent phenomena, and that it agrees with the mechanical definition of inertial coordinates. As always, the "laws of motion" serve first as definitions of the coordinates, and then as laws. |
|
|
|
Many texts include statements that attempt to identify how reference frames are actually defined, but they almost invariably fail to include the specification of the time coordinate. For example, the article on mechanics in the Encyclopedia Britannica says |
|
|
|
The subject of kinematics requires the concepts of position, time, and the derived concepts of velocity and acceleration. Definitions of length and time interval must first be given… The primitive terms [such as “distance”] acquire physical meaning when they are given an operational definition: one that specifies how they are to be measured… A coordinate system (frame of reference) must be specified with respect to which the measurements are to be made. Newton did not offer a very satisfactory frame of reference within which velocities and accelerations are to be measured. Perhaps it is best to postulate that there is some reference system with respect to which the laws of motion are valid, leaving its determination to experiment. Such a frame of reference is called an inertial system. |
|
|
|
This is all reasonable – except that kinematics need not be restricted to inertial coordinate systems, so what this passage should really be referring to is the coordinate systems used to express the relations of kinetics. (Recall that kinematics “does not involve any physical laws such as Newton’s laws”.) Greenwood too acknowledges that the coordinate systems (which he goes on to use tacitly in his discussion of kinematics) are based on physical laws, when he says |
|
|
|
The approach we shall take is to define an inertial or Newtonian reference frame to be any rigid set of coordinate axes such that particle motion relative to these axes is described by Newton’s laws of motion. |
|
|
|
As discussed above, Einstein’s 1905 paper on the electrodynamics of moving bodies begins with a similar statement, asking us to consider a system of coordinates in terms of which the equations of Newtonian mechanics hold good (at least quasi-statically). From the modern point of view, following Minkowski, we are used to regarding coordinate systems as including time as well as space coordinates, but unfortunately this was not yet Einstein’s view in 1905, and it is still not fully assimilated by modern writers, who continue to think (at least some of the time) of frames and coordinate systems as referring only to spatial measures. This was a habit into which scientists fell during the two centuries when Newtonian mechanics held sway (and the inertial basis of temporal synchronization was often overlooked, since it seemed to give a unique answer, and hence could be mistaken for an apriori category), and it continues to pervade physics textbooks today, creating endless confusion. Using just the first law of motion to define inertial coordinate systems (regarded as spatial systems of measure only), we are left with an ambiguity in the time coordinate. Of course, the time coordinate is completely determined by stipulating that all the laws of motion (not just the first) are satisfied, but very few authors articulate this important fact. Instead, they usually leave the physical basis of the time coordinates un-discussed in classical mechanics, and when special relativity is introduced they claim that we can only constrain the time coordinate of an inertial coordinate system by arbitrarily stipulating that the speed of light is isotropic. Thus students are given the false impression that there was never any need to define the time coordinate physically prior to the advent of special relativity, whereas in fact it had always been defined by the laws of motion, just as are the space coordinates. |
|
|
|
In a purely kinematical sense, excluding any reference to inertial frames and physical laws, the velocity and acceleration of a particle are entirely dependent on the choice of coordinate systems. In this context velocity and acceleration can only be defined as the first and second derivatives of the space coordinates with respect to the time coordinate, and these have no physical significance for purely arbitrary coordinates. This is why Greenwood says kinematics is purely mathematical, because, taken literally, it has no physical significance at all. And yet it is typically presented as if it does have physical significance, specifically, as if it represents the motions of physical objects (albeit without regard to the “causes” of motion). This is not true, because with no restriction on the physical significance of the coordinates and terms of description it cannot be referring to any representation of physical phenomena. The reason for the confusion is that many writers tacitly have in mind inertial coordinate systems, i.e., Cartesian spatial coordinates with a Euclidean metric and a time coordinate synchronized in accord with the requirement for the laws of mechanics to hold good. This misconception can be traced back to the unexamined belief that our systems of reference are somehow apriori concepts. |
|
|
|
The mis-use of the term “kinematic” to describe the relations of special relativity has unfortunately propagated into much of the subsequent literature, despite that fact that in every case (just as in Einstein’s original paper) the labeling of the relations as “kinematic” is invariably followed immediately by a description that explicitly reveals them to be dynamical (kinetic). To give just one more example, in his book “Essential Relativity”, Rindler begins his discussion of special relativity with a chapter entitled “Einsteinian Kinematics”, and yet the discussion in that section is based entirely on a coordinate lattice established kinetically, e.g., synchronizing clocks using either “standard projectiles [fired] from standard guns” or light pulses, both of which are inertial (and hence kinetic) phenomena. Now, one might argue that the inertia of energy and all the associated dynamical consequences for projectiles fired from guns, etc., are encoded in the Minkowski metric of spacetime, and could therefore be regarded as kinematic, based on the idea that the Minkowski metric reduces inertia itself – formerly regarded as the hallmark of kinetics – to a matter of pure kinematics and the ‘geometry’ of spacetime. For example, we might point to the fact that the proper time along a worldline with some non-zero speed is reduced relative to the coordinate time, and assert that the acceleration in response to an applied force is to be evaluated in terms of the proper time. This is a fair description, but it is not consistent with the meaning of the word kinematics, which (as explained above) refers to purely mathematical propositions with no physical content. The slowing of proper time along a moving worldline manifests itself only as phenomena that involve interactions and response to forces, which is the very definition of dynamics (kinetics). The fact that we can arbitrarily define a family of coordinate systems consistent with the relativistic speed composition formula does not imply that spacetime has a Minkowskian metric. Establishing the spatial metric of a geometrical manifold, or the spatio-temporal metric of spacetime, necessarily involves physical behavior and dynamical (kinetic) interactions. It is an empirical fact that space-time coordinate systems that are inertial (in the full sense of that word) are related by Lorentz transformations, but the converse is not true: Coordinate systems (in a given region of space-time) related by Lorentz transformations need not be inertial. |
|
|
|
Incidentally, since Einstein originated the use of the word “kinematic” to characterize the relations of special relativity, it’s worth noting his comments on that word in his 1907 review article. In section 2 of the paper (entitled “General Remarks Concerning Space and Time”) he defined the “geometric shape” of an object as the locus of simultaneous points of the object for a system of inertial coordinates in which the object is at rest. Of course, this is with the understanding that simultaneity is based on the stipulated isotropy of inertia. Then he defined the “kinematic shape” of an object as the locus of simultaneous points of the object for a system of inertial coordinates in which the object is in motion – but this again is based on the dynamically defined simultaneity based on inertial isotropy, so labeling this as a kinematic effect is contradictory to the actual definition of the word “kinematic”. According to Einstein’s usage, the relativistic length contraction of an object would be called a kinematic effect, but the effect is clearly not kinematic according to the normal definition of that word. Simply defining a family of coordinate systems related by Lorentz transformations (for example) does not have any physical significance. Length contraction is not simply an artifact of coordinates with no physical meaning. The physical meaning of length contraction is that it represents the spatial extent in terms of a relatively moving system of inertial coordinates, defined as space and time coordinates in which inertia is homogeneous and isotropic, so the equations of Newtonian mechanics (for example) are at least quasi-statically valid. This is what gives length contraction its physical significance, and it is directly based on the dynamic (kinetic) behavior of physical entities (both material and electromagnetic). |
|
|
|
It might be argued that within the bounds of kinematics we can define the metric of spacetime, without invoking any dynamics, and that the Minkowski metric entails all the relativistic effects that are properly called kinematic. However, just as the geometry of space (as a description of physical relations, not as an axiomatic structure) is ultimately based on physical phenomena, so too is the metric of spacetime. In fact, the spacetime metric involves even more aspects of physical phenomena than does a purely spatial metric, because it must include dynamics (kinetics) to establish the measures of space and time, as well as the relationships between those measures. When we write the Minkowski metric (dt)2 = (dt)2 – (dx)2, the symbols t and x represent inertial coordinates. The expression has no meaning unless we know what an inertial coordinate system physically means. (Of course, with another choice of coordinates and the corresponding metric coefficients we could express the same proper time element, but this is just a formal re-writing of the diagonal form, which represents the actual physical content.) Another way of saying this is that special relativity consists of the assertion that inertial coordinate systems are related by Lorentz transformations, but (as noted above) we cannot reverse this and define inertial coordinate systems as systems related by Lorentz transformations. To prove this, simply notice that we can take any arbitrary non-inertial coordinate system in some region of spacetime, and apply a Lorentz transformation to give a new coordinate system in that region, but this does not make either of them inertial coordinate systems. |
|
|
|
Perhaps the main reason people are tempted to characterize the relativistic relations between energy, mass, and momentum as “kinematic” is that the key dynamical relation |
|
|
|
|
|
|
|
can be seen as just a re-scaled expression of the metrical line element |
|
|
|
|
|
|
|
If the latter was purely kinematic, then one could argue that the former must also be kinematic. However, this is backwards, because what the connection between these two relations actually reveals is the dynamical meanings of the line element, as explained above. Also, since the traditional definition of “kinematics” explicitly excludes considerations of mass, energy, and momentum, it would seem to be an inappropriate word to characterize the (admittedly generic) relationship between mass, energy, and momentum. The most we could say is that special relativity undermines the distinction between kinematics and dynamics. (The distinction was also untenable in Newtonian physics, but this was easier to overlook in the absence of a mass-energy relation and with the conceivability of arbitrarily large rigid bodies). |
|
|
|
It is sometimes claimed that length contraction cannot be dynamical because it exists for a given isolated object relative to different frames of reference, without applying any external force or influence to the object. Thus it is claimed that length contraction is purely an artifact of the terms of description, since nothing is physically happening to the object. We are simply describing it in terms of different coordinate systems, in some of which it is moving (and hence exhibits length contraction) and in some of which it is at rest (and exhibits no length contraction). But this is wrong, for two closely related reasons. First, as explained above, the very definitions of those coordinate systems are based on dynamics, which is what gives them their physical significance. Second, length contraction does not consist exclusively of considering isolated objects in terms of different coordinate systems. That would be just one hand clapping. The other (crucial) aspect of length contraction is that if we consider some equilibrium configuration of matter (established and maintained by the laws of physics) such that the aggregate is periodically oscillating about a configuration that is at rest in one inertial coordinate system, and if we then impart a velocity v to the components of this configuration (gently enough so as not to permanently scramble or distort the configuration), and allow it to reach equilibrium in the new state of aggregate motion, the resulting configuration described in terms of the original inertial coordinates will be identical to the description of the original configuration in terms of a coordinate system in which the original configuration had the velocity v. In other words, what gives the purely descriptive length contraction (of an isolated object in terms of different coordinate systems) its physical meaning is that it corresponds exactly to how the dynamical laws of physics affect actual objects. (For more a more thorough discussion, see Length Contraction, Passive and Active.) |
|
|
|
By the way, Janssen criticizes the neo-Lorentzians for thinking there was value in the repetitions of the Michelson-Morley experiment performed by Morley and Miller during the years from 1900 to 1905, using devices constructed with different substances (e.g., steel, wood, brass). Janssen says these experiments were a waste of time, because the null outcome was already implied by the two postulates of special relativity, independent of the “dynamical” details. I’m inclined to agree that the experiments of Morley and Miller were somewhat misguided and not well motivated, but on the other hand I don’t think they can be dismissed as totally worthless. It’s true that if we accept the postulates of special relativity, then the outcome of such experiments is a foregone conclusion, independent of the detailed construction of the devices. However, such experiments can be regarded as tests of the postulates of special relativity, i.e., tests of Lorentz invariance. Even if we concede that the Lorentz invariance of mechanical inertia and electromagnetism had already been sufficiently established by 1900, one could still have legitimately questioned the Lorentz invariance of whatever forces maintain the structure of different substances. It is apriori conceivable that the strong nuclear force, the weak nuclear force, quantum “exchange forces”, and/or the gravitational force might not be perfectly Lorentz invariant. Of course, any violation of Lorentz invariance would imply that one or the other (or both) of the two postulates of special relativity was invalid, but this is an empirical question. Lorentz invariance is not tautological, it is established by experiment and observation, and could conceivably be falsified (as Einstein himself said). |
|
|
|
Indeed, a very ambitious repetition of the Michelson-Morley experiment, using fantastically sensitive interferometers, is presently being conducted to see if fringe shifts arising from gravitational effects can be detected. According to special relativity there can be no such effect, and yet presumably Janssen doesn’t regard the LIGO experiments as another “textbook example of the waste of time and resources that can occur if experimenters rely on faulty explanations to guide them in their work”. Global Lorentz invariance actually is violated by gravity according to general relativity, which illustrates the fact that Lorentz invariance is not tautological. Whether there was any justification for suspecting (back in the days before the quantum theory and nuclear forces were understood as well as they are today) that there might be some detectable violation of Lorentz invariance in the different responses of brass and steel is, to some extent, a matter of scientific taste. I personally would not have thought such suspicions were justified, for two reasons. First, the principle of special relativity is so rationally compelling, like the principle of energy conservation, that I would be astounded if it were found to fail (locally). It is a very robust organizing principle. Second, the undetectability of the ether wind had already been shown in a variety of circumstances, making it highly implausible that any violation was near at hand. We might compare the work of Morley and Miller to that of modern scientists who strive to conduct “loophole-free” tests of Bell inequalities, or with hypothetical neo-Lorentzians trying to determine if the non-relativistic Schrodinger equation is actually correct (rather than working to develop the relativistic Dirac equation). As a matter of scientific taste, I would not regard these as very promising avenues of research, and the principles of special relativity seem to be a much more robust foundation on which to base our thinking. Nevertheless, the on-going experiments to test Lorentz invariance, and the LIGO activity, attest to the fact that Lorentz invariance and the principles of special relativity are not tautological – in the same sense that the conservation of energy is not tautological. As Einstein said, reflecting on the foundations of special relativity: |
|
|
|
With the given physical interpretation of coordinates and time, this is by no means merely a conventional step, but implies certain hypotheses concerning the behavior of moving [physical entities] which can be experimentally confirmed or disproved. |
|
|
|
Recalling that, according to the traditional definition, kinematics “is purely mathematical in nature and does not involve any physical laws”, it’s clear that the relations of special relativity are not kinematic according to the traditional definition of that word. |
|
|