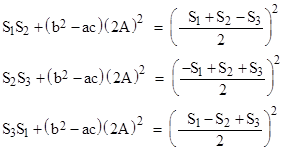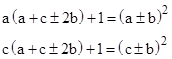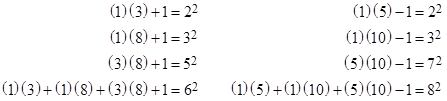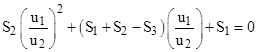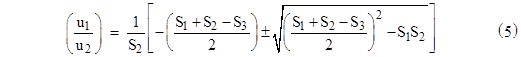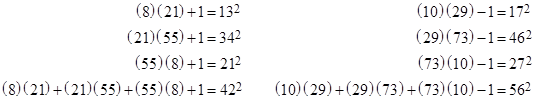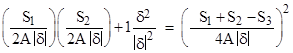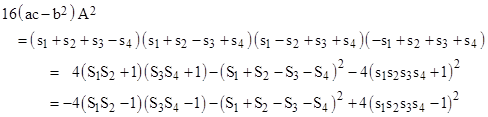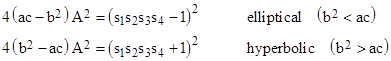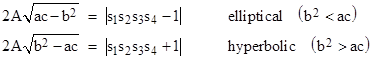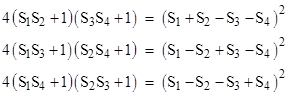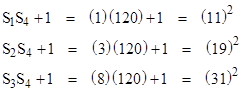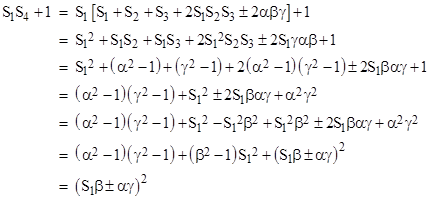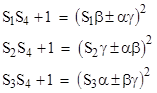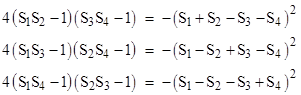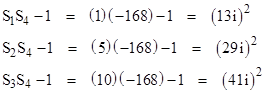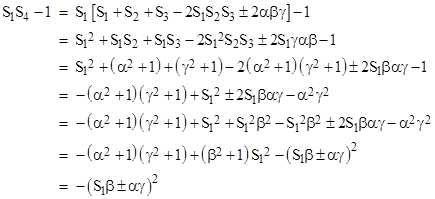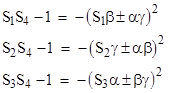Diophantine n-tuples and Their Duals

Diophantus considered rational solutions of the system of equations

An infinite class of solutions (though not all solutions) can be developed from formulas for the areas of triangles expressed in terms of generalized “edge lengths”. Given an arbitrary triangle, let (u₁,v₁), (u₂,v₂), and (u₃,v₃) denote the components of the three edge vectors going clockwise around the triangle, in terms of some Cartesian coordinate system. Since these vectors form a closed loop, we have u₁+u₂+u₃ = 0 and v₁+v₂+v₃ = 0. Now let s_j denote the generalized “edge length” defined as

for given constants a,b,c. (If we take a = c = 1 and b = 0, these are simply the actual lengths of the edges.) The area A of the triangle is given by any of the three equivalent expressions

By the generalized version of Heron’s formula, the area of the triangle is also given by

If we define s = (s₁ + s₂ + s₃)/2, this can be expressed more compactly as

To show how this formula gives Diophantine triples, let us define S_j = s_j², and then expand the products on the right hand side and multiply through by 4 to give

This can be re-written in several equivalent forms, including

These three expressions show that the set of numbers {S₁,S₂,S₃} constitutes a solution of the problem of Diophantus mentioned above, with k = (b²−ac)(2A)².  Incidentally, the above relations can also be written in the explicitly symmetrical form

In the special case when k = 1 the integers {S₁,S₂,S₃} are called a Diophantine triple, and equation (1) reduces to

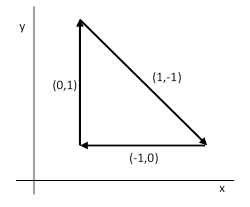
To illustrate, consider the triangle depicted below

The area of this triangle is A = 1/2, and the edge vectors are (u₁,v₁) = (0,1), (u₂,v₂) = (1,−1), and (u₃,v₃) = (−1,0), so the S_j values are

If we now choose a,b,c such that the discriminant of the quadratic form defining the S_j values is unity, then these values will constitute a Diophantine triple. Therefore we need only choose integers a,b,c such that b² – ac = 1, which is equivalent to ac + 1 = b². Of course this condition is independent of the sign of b, so given any Diophantine 2-tuple {a,c} with ac + 1 = b², we have the Diophantine 3-tuples {a, c, a+c−2b} and {a, c, a+c+2b}. This is easily verified by noting that

The same result can also be reached directly by simply solving the basic identity (2) for any one of the S_j values in terms of the other two. For example, if we solve (2) for S₂ we get

This shows that if S₁,S₂,S₃ satisfy (2) then S₁S₃ + 1 must be a square, and by symmetry so must be S₁S₂ + 1 and S₂S₃ + 1, which confirms that every solution of (2) in integers represents a Diophantine 3-tuple. These are called regular Diophantine 3-tuples, to distinguish them from Diophantine 3-tuples that are not solutions of (2). The above discussion also shows that every regular Diophantine 3-tuple can be found by starting with a 2-tuple {a,c} and then extending it to a 3-tuple as described above.

It’s interesting that regular Diophantine 3-tuples can be represented by triangles in two very different ways. First, as we’ve just described, they can all be represented by the generalized Heron formula based on the same primitive triangle depicted above, by simply choosing different coefficients a,b,c for the quadratic form of the generalized edge length definition such that b² – ac = 1. But they can also be represented for any fixed choice of coefficients a,b,c by choosing different triangles of area 1/2 with rational edge vectors. To illustrate, consider the simplest non-trivial Diophantine triple {1,3,8}. In order to represent this in terms of the primitive triangle shown above, we would select coefficients of the generalized length function a = 1 and c = 3, and then we must have b = ±2. Thus our generalized squared edge length function is

Inserting the edge vector components for our standard primitive triangle (depicted above), we get S₁ = 3, S₃ = 1, and S₂ = 0 or 8. But there is another way of representing the triple {1,3,8}, using a standard edge length definition and selecting a suitable triangle. Let us take b = 1/2 and a = c = 0 as our standard coefficients, so the square edge lengths are simply

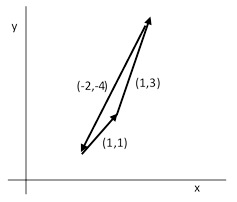
Now we need a triangle whose area is A = 1, and for this we can take the triangle depicted below.

With these edge vector components and generalized length definition we have S₁ = 1, S₂ = 3, and S₃ = 8, and it’s easy to verify from equation (0) that the area is 1. In this same way we can represent any regular Diophantine triple by a triangle of area 1 with integer edge vector components, always using the standard generalized length definition given by equation (3).

The fact that regular Diophantine triples can be represented by a standard triangle with variable quadratic forms, or alternatively by a standard quadratic form with variable triangles, is reminiscent of how quantum mechanical systems can be represented by a constant state vector with variable measurement operators, or alternatively by standard measurement operators with variable state vectors.

So far we’ve focused mainly on the case when (b²−ac)(2A)² = 1, corresponding to Diophantine triples. If, instead, we choose a quadratic form such that 4(b²−ac)A² = −1, then S₁, S₂, S₃ constitute what might be called an anti-Diophantine triple, because each of their pairwise products reduced by unity is a square. For this purpose we replace (3) with the definition

Just as the s_j based on (3) are the geometric mean of u_j and v_j, the definition of s_j based on (4) is the root-mean-square. In this case we have a = c = 1/2 and b = 0. We again want a triangle with squared area equal to 1, and with integer edge components (with the same parity), so we can use the same triangle we used for the previous case. Inserting the edge vector components u₁ = v₁ = 1, u₂ = 1, v₂ = 3, u₃ = −2, v₃ = −4, into equation (4), we get the anti-Diophantine triple S₁ = 1, S₂ = 5, S₃ = 10. This is the dual of the Diophantine triple {1,3,8}. A summary of these dual triples is shown below.

One might wonder if, for any given regular triple and any given quadratic form, we can infer the components of the edge vectors of a corresponding triangle. Let us take the quadratic form (3) as an example. We know that u₁+u₂+u₃ = 0, and similarly v₁+v₂+v₃ = 0, so we can substitute –(u₁+u₂) and –(v₁+v₂) for u₃ and v₃ respectively into the last condition to give the system of equations in four variables

Solving the first two equations for v₁ and v₂, substituting into the third, and re-arranging terms, we get

We can then solve this quadratic for (u₁/u₂) to give

We recognize the argument of the square root as our previous expression for the squared area of the triangle, which in this case is 1. Inserting the values of S_j for this example, we get u₁/u₂ = 1 or 1/3, and so this implies the u values 1,1,−2 or else 1,3,−4, and whichever set we choose, the v_j values are the other set. Using the first choice, we have u₁ = v₁ = 1, u₂ = 1, v₂ = 3, u₃ = −2, v₃ = −4.

For a less trivial example, consider the Diophantine triple S = {8,21,55}. Inserting these values into equation (5) we get u₁/u₂ = 2/3 or 4/7, so we take u = {2,3,−5} and v = {4,7,−11} to give the anti-Diophantine triple S = {10,29,73}. For these triples we have the results

Incidentally, we could describe the usual Diophantine triples as “hyperbolic”, and the anti-Diophantine triples as “elliptical”, because they correspond respectively to the cases where the discriminant b² – ac of the quadratic form is positive or negative, and hence the locus described by the quadratic form is respectively a hyperbola or an ellipse. If we were interested only in rational solutions, then for any quadratic form with a rational square determinant, i.e., with b² – ac = δ² or else ac – b² = δ² where δ is a positive rational number, we could divide through each of the basic triple equations and write them in the form

Thus every triangle (of any area) with rational edge vector components, and with any rational quadratic form (hyperbolic or elliptical), corresponds to a rational Diophantine or anti-Diophantine triple.

It’s natural to try to extend these triples by progressing from the generalized Heron formula for the area of a triangle to the generalized Brahmagupta formula for the area of a quadrilateral (whose vertices lie on a locus with the given quadratic form) in terms of the components of the edges. Thus we’re led to consider a 4th edge vector with components u₄,v₄, and to define s₄ and S₄ in terms of the chosen quadratic form of these components. Of course, we now have the loop conditions u₁ + u₂ + u₃ + u₄ = 0 and v₁ + v₂ + v₃ + v₄ = 0, so in general no three of the vectors form a closed loop, and hence no subset of the S_j values need be a regular triple, even though they constitute a triple.

According to the generalized Brahmagupta formula, the squared area of a quadrilateral whose vertices lie on a locus of the quadratic form a(x-x₀)² + 2b(x-x₀)(y-y₀) + c(y-y₀)² = r² is given by

which of course reduces to Heron’s formula for the area of a triangle if any of the edge vectors are null, i.e., if s_j = 0. The right hand side can be expanded and the resulting terms collected in several different ways. All but one of the terms involve only the squared parameters s_j². The exception is the term 8s₁s₂s₃s₄. The area formula for a general quadrilateral (with vertices not necessarily on a locus of the given quadratic form) includes on the right hand side the term -16u₁u₂u₃u₄cos(θ)² where θ is half the sum of two opposite angles, so we could cancel these terms if we specialized to quadrilaterals with θ = π/4. However, rather than take this approach, we will continue to focus on quadrilaterals inscribed in the given quadratic form, and isolate the exceptional term in such a way that it can be absorbed into a simple condition on the area A. To do this, we arrange the terms of the product in either of the following two ways:

The overall expression is explicitly symmetrical in the four parameters, as is the last term on the right side of each expression, so the sum of the first two terms must also be symmetrical, as can be confirmed by expanding them. This motivates our partitioning of the terms in this way, since we seek a symmetrical expression (analogous to (1) above) involving the four S_j values. We’ve developed two different expressions because we want to equate the final square terms to the quantity 16(ac−b²)A², which is positive or negative depending on whether the quadratic form is hyperbolic or elliptical. Thus for these cases we impose the condition

which can also be written as

Now, for the hyperbolic case, given any triple {S₁,S₂,S₃}, which need not be regular, we can compute the value of S₄ that satisfies this condition, which implies that the sum of the first two terms on the previous expressions must vanish. Thus we compute the value of S₄ such that each of the following three equivalent equations is satisfied

Solving this quadratic condition for S₄ we get

This shows that if {S₁,S₂,S₃} is a Diophantine triple, then S₄ is an integer, because each of the three factors under the square root sign is a square. Furthermore, the three preceding equations imply that each of the quantities S₁S₄ + 1, S₂S₄ + 1, and S₃S₄ + 1, is a square, so {S₁,S₂,S₃,S₄} is a Diophantine 4-tuple. For example, beginning with the Diophantine triple {1,3,8}, we compute S₄ = 0 or 120. The fact that one of the S₄ roots is zero signifies that the original triple is regular. Taking the non-trivial root S₄ = 120, we have

To find the explicit expression for these three squares in this case (originally found by Arkin, Hoggatt, and Strauss in 1979), by the initial Diophantine triple conditions we have integers α,β,γ such that

and we can evaluate the first condition involving S₄ as

Hence by symmetry we have

Similarly for the elliptical case we have the quadratic condition represented by each of the three equivalent expressions

Solving this quadratic condition for S₄ we get

This shows that if {S₁,S₂,S₃} is an anti-Diophantine triple (not necessarily regular), then S₄ is an integer, because each of the three factors under the square root sign is a square. Furthermore, the three preceding equations imply that each of the quantities S₁S₄ – 1, S₂S₄ – 1, and S₃S₄ – 1, is a square, albeit of an imaginary integer (because S₄ is negative). We will call such a set of four numbers an anti-Diophantine 4-tuple. As an example, beginning with the triple {1,5,10} we compute S₄ = −168, for which we have

To find the explicit expression for the (negative) squares in this case, by the initial anti-Diophantine triple conditions we have integers α,β,γ such that

and we can evaluate the first condition involving S₄ as

Hence by symmetry we have

Since these expressions give negative squares, these 4-tuples do not represent anti-Diophantine 4-tuples in real integers, although they do in Gaussian integers. It appears that there are no anti-Diophantine 4-tuples in real integers.

Return to MathPages Main Menu