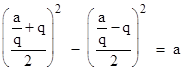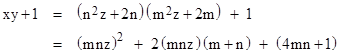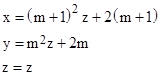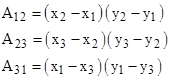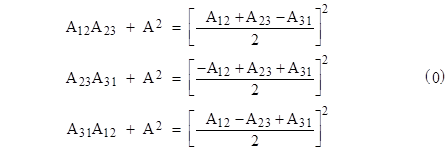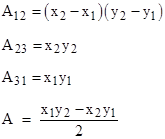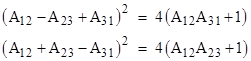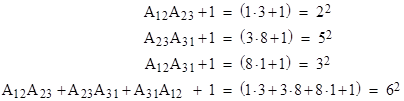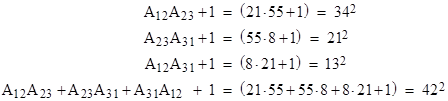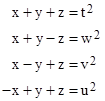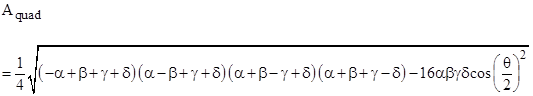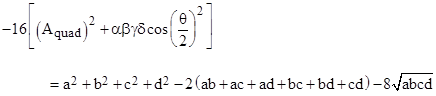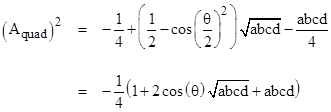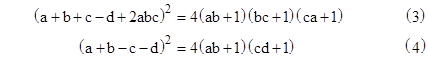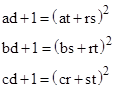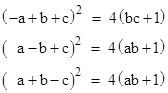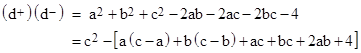Triangles and Diophantine n-tuples

Diophantus considered sets of rational numbers such that each pairwise product augmented by a single constant is a square. For example, in III,10 he sought numbers x,y,z and a such that xy+a, xz+a and yz+a are rational squares. In other words, he sought a rational solution of the system of equations

He noticed that if we set

then we have xy = α², xz = β², and yz = γ², so the problem is equivalent to finding a rational solution of the equations

This is easy, because for any rational number q we have

Consequently for any three rational numbers q₁, q₂, q₃ a solution is given by

Later, in VI,19, Diophantus considered the special case of this problem with a = 1. The above solution is still applicable, but of course it generally leads to solutions in fractional numbers. For the special case with a = 1 Diophantus (as reported by Heath) took a different approach. He noted that if we can set x = n²z + 2n and y = m²z + 2m for any z and any numbers n,m, then we have

so we will have a complete solution if we choose m,n,z such that the quantity

is a square. Clearly this quantity equals the square of (mnz+m+n) if 4mn+1 = (m+n)², which is equivalent to the condition (m−n)² = 1. Thus Diophantus could take n = m+1 to give the solution

For example, with z = m = 1 this gives the integer solution x = 8, y = 3, z = 1. Any set of three integers x,y,z such that xy+1, xz+1, and yz+1 are squares is called a Diophantine triple. (If x,y,z are not integers but are rational, they are called a rational Diophantine triple.)

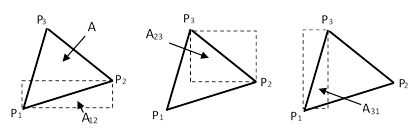
It’s interesting that solutions of these systems of equations arise naturally in relation to the areas of triangles. Consider a triangle whose vertices P₁, P₂, P₃ have the integer coordinates (x₁,y₁), (x₂,y₂), (x₃,y₃), and let A₁₂, A₂₃, and A₃₁ denote the areas of the rectangles (oriented with the coordinate axes) whose diagonals are the edges of the triangle, as indicated in the figures below.

Thus we have

and of course the area of the triangle itself is

By simple algebra we can verify the identities

Thus for any lattice triangle (i.e., a triangle with integer coordinates) with area A = 1 we have a corresponding Diophantine triple. Obviously none of the areas is affected by a translation of the triangle, so without loss of generality we can place P₃ at the origin, so we have x₃ = y₃ = 0, and the expressions for the areas simplify to

As mentioned above, for a lattice triangle (i.e., with integer coefficients), the quantities A₁₂, A₂₃, A₃₁ represent a Diophantine triple if A² = 1, which is true if and only if the coordinates of the vertices satisfy the condition

To express this condition in terms of the numbers A₁₂, A₂₃, and A₃₁ we expand the left side and write the relation as

and thus we have

Equivalently we can also write this in the forms

These expression are consistent with the fact that the quantities in parentheses on the right hand sides are squares. Also, if we expand the left hand side (of any one of these equivalent expressions) and re-arrange terms, we can express this relation in the explicitly symmetrical form

This last relation shows that the quantity in parentheses on the right side is also a square. For a simple example, consider the triangle with vertices P₁ = {2,4}, P₂ = {1,3}, and P₃ = {0,0}. The area of this triangle is (x₁y₂ – x₂y₁)/2 = (2∙3 – 1∙4)/2 = 1, so it satisfies the requirement for unit area. The areas of the three rectangles circumscribing the edges are A₁₂ = 1, A₂₃ = 3, and A₃₁ = 8. As expected, we have the squares

For another example, consider the triangle with vertices P₁ = {2,4}, P₂ = {5,11}, and P₃ = {0,0}. The area of this triangle is (x₁y₂ – x₂y₁)/2 = (2∙11 – 4∙5)/2 = 1, so it satisfies the requirement for unit area. The areas of the three rectangles circumscribing the edges are A₁₂ = 21, A₂₃ = 55, and A₃₁ = 8. As expected, we have the squares

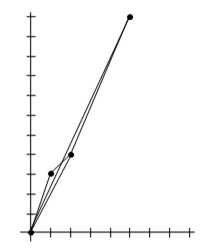
The triangles for these two examples are depicted in the figure below.

The above formulas were based on the expression for the area of a triangle in terms of the Cartesian coordinates of the vertices, but it’s interesting to note that the formulas also exhibit a connection with Heron’s formula for the area of a triangle in terms of its edge lengths. Recall that if a,b,c are the edge lengths of a triangle, then the area of the triangle is

Thus if we consider a triangle whose edge lengths a,b,c are numerically equal to the quantities A₁₂, A₂₃, A₃₁ then the above formulas imply that the squared area (A′)² of this meta-triangle is the integer

We call this a “meta-triangle” because of the change of units, since the edge lengths are equated with areas from the plane of the original triangle. We could regard the edges as cross products of the components of the edges of the original triangle. (This is reminiscent of the fact that if the volume of a parallelepiped with adjacent edge vectors A, B, C is V then the volume of the parallelepiped with adjacent edge vectors AxB, BxC, CxA is simply V².)

Incidentally, it seems that the inspiration for some of Diophantus’ problem may have been attempts to find triangles with rational areas based on Heron’s formula, because in III,5 he considered the following system of four equations

According to Heron’s formula, a triangle with rational edge lengths x,y,z would have rational area if these equations are satisfied. Diophantus noted that we need only find three squares whose sum is a square, because if we have u² + v² + w² = t² then a solution to these four equations is given by

Another very close connection between Diophantine triples and Heron’s formula for triangle areas can be seen if we define a triangle with edge lengths α, β, γ equal to the square roots of the areas of the three rectangles circumscribing the edges of our original triangle. In other words, we consider the (imaginary) triangle with edge lengths

Thus α, β, γ are the geometric means of the components of the edges of the original triangle. We call this an imaginary triangle because the edge lengths need not satisfy the triangle inequality, and the area of the triangle may be imaginary. In terms of these lengths (which have the same dimension of length as the edges of the original triangle), any of the equations (0) can be re-arranged and factored to give

The left hand side is simply Heron’s formula for the area of a “triangle” with edge lengths α,β,γ, so this equation signifies that the area of this imaginary triangle, with edge lengths equal to the geometric mean of the orthogonal components of the edges of the original triangle (for any orientation) is i/2 times the area of the original triangle. In particular, the condition that the original triangle have squared area equal to 1 is equivalent to the condition that this alternate triangle have squared area equal to −1/4.

This is particularly interesting because it immediately suggests a way of extending these formulas to a set of four quantities. Recall that Heron’s formula for the area of a triangle is really just a special case of the formula for the area of a quadrilateral with edge lengths α, β, γ and δ. The general formula is

where θ is the sum of two opposite interior angles. The squared area of a quadrilateral is therefore given by

where a = α², b = β², c = γ², and d = δ². For a quadrilateral inscribed in a circle (called a cyclic quadrilateral) we always have θ = π, so the cosine term drops out. To eliminate the irrational quantity represented by the square root of abcd, we need the left hand side to include this quantity. Also, we want (A_quad)² to be a square quantity for a cyclic quadrilateral, equal to −1/4 when d = 0, so we complete the square to give the stipulation

or equivalently

Thus for a cyclic quadrilateral (θ = π) with edge lengths α, β, γ , δ, this amounts to the condition that the area equals

This condition is equivalent to the Diophantine 4-tuple relation

which can also be written in either of the two forms

Both of these expressions are invariant under permutations of the four variables. It follows from (3) that if ab+1, bc+1, and ca+1 are squares for integers a,b,c, then d is also an integer – actually one of two integers, accounting for the two possible signs when taking the square root – given by the well-known formula (Arkin, Hoggatt, and Strauss)

Also, equation (4) confirms that, if ab+1 is a square, then so must be cd+1. In addition, since (4) is fully symmetrical under permutations of the variables, we can permute them such that the two quantities in parentheses on the right side are ac+1 and bd+1, or else bc+1 and ad+1. Thus, given integers a,b,c such that ab+1 = r², ac+1 = s², and bc+1 = t² for integers r,s,t, it follows that ad+1, bd+1, and cd+1 (where d is given by (5)) are also squares. Explicitly we have

In summary, for any given Diophantine triple a,b,c, we can construct two Diophantine 4-tuples, consisting of {a,b,c,d⁻} and {a,b,c,d⁺}, where d⁻ and d⁺ are the two values of d given by equation (5). Both of these 4-tuples satisfy equations (2), (3), and (4), and their permutations, which are all algebraically equivalent to each other. Clearly d+ is positive and exceeds the sum of a, b, and c. However, the value of d⁻ may be zero or negative. If d^- equals zero, then {a,b,c} constitute a regular Diophantine triple, satisfying the reduced equation

which is equivalent to equation (1). As we’ve seen, every solution of (6) in non-negative integers is a Diophantine triple, because (6) is algebraically equivalent to each of the expressions

so we know immediately that ab+1, ac+1 and bc+1 are squares. However, it’s less obvious that every solution of equation (2) (in any of its equivalent forms) is a Diophantine 4-tuple. A proof, based on one pointed out by Phil Gibbs, that every solution of equation (2) in positive integers is indeed a Diophantine 4-tuple, is as follows.

Let a, b, c, d⁺ denote four positive integers, in non-decreasing order, that satisfy equation (2). By equation (5) there is another integer, which we call d^- such that {a,b,c,d⁻} also satisfies (2). Furthermore, equation (5) implies

and since the quantity in square brackets is positive (because a,b,c are positive in non-decreasing order) it follows that (d⁺)(d⁻) is less than c², and therefore, since d⁺ is greater than or equal to c, we see that d^- is strictly less than c. On the other hand, equation (4) with d = d⁻ implies that d^- must be non-negative, since the left side is non-negative and 4(ab+1) is positive, so c(d⁻) + 1 must be positive or zero. It is positive if and only if d⁻ = 0, which we’ve already covered, so the only remaining possibility is c(d⁻) = -1, which implies c = 1 and d^- = -1, but we know a,b,c are positive integers in non-decreasing order, so this would imply a = b = c = 1 with d⁻ = −1, which is not a solution. Consequently, if d⁻ is not zero, we know that one of the sequences{d⁻,a,b,c}, {a,d⁻,b,c}, or {a,b,d⁻,c} constitutes a solution set of four positive integers in non-decreasing order whose sum is strictly smaller than the sum of a,b,c,d⁺. We can repeat this process, producing a sequence of strictly smaller solutions of (2) in positive integers (arranged in non-decreasing order), and eventually we must arrive at a case where d⁻ is zero. In this case we know the corresponding a,b,c constitute a Diophantine triple from purely algebraic considerations as discussed above, and augmenting such a triple with 0 produces a (trivial) Diophantine 4-tuple. Thus every set of four positive integers that satisfy equation (2) is related in this way to a Diophantine 4-tuple. It follows that every such positive integer solution of (2) is itself a Diophantine 4-tuple, because if d⁻ is a Diophantine 4-tuple then a,b,c is necessarily a Diophantine triple, and we’ve already seen that this implies a,b,c,d⁺ is a Diophantine 4-tuple.

Return to MathPages Main Menu