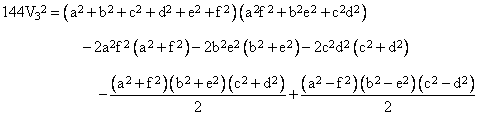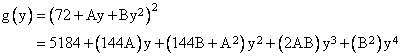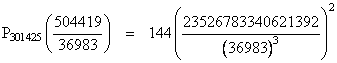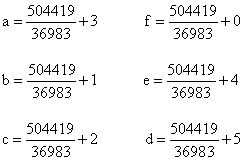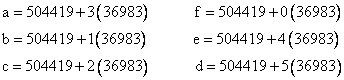Tetrahedra with Edges in Arithmetic Progression

As discussed in the note on simplex volumes, the volume of a tetrahedron with edge lengths a = L₁₂, b = L₁₃, c = L₁₄, d = L₂₃, e = L₂₄, and f = L₃₄ is given by the relation

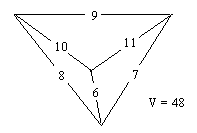
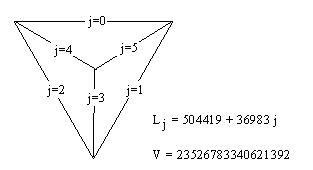
It so happens that there exists a tetrahedron with the six consecutive integer edge lengths 6,7,8,9,10,11 for which the volume equals the integer 48.  Of course, since the above formula is not symmetrical in the edge lengths, the order in which we assign the values is important. We get the stated volume with the assignments a=6, b=7, c=8, d=11, e=10, f=9, as depicted schematically in the figure below.

This is the only known set of consecutive integer edge lengths for which the tetrahedron volume is an integer. In fact, we might ask whether, aside from this example (and trivial integer multiples of it), there exists any other sequence of integer edge lengths in arithmetic progression that yield an integer volume. The answer is yes, but they are quite rare.

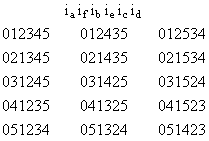
The number of distinct ways of assigning a given set of values to the six edge lengths is 30, because there are 15 ways of pairing the edges (there are five choices of partners for the first number, and then three choices for the next, and only one choice for the last), and each of these pairings can give two distinct volumes, by transposing the terms of any pair. (These transpositions simply change the sign of the last term in the above equation.) We begin by considering the possibility of consecutive integer solutions for any of these 30 possible arrangements. This means we need to assign the values x, x+1, x+2, x+3, x+4, and x+5 to the variables a,b,c,d,e,f in each of the 30 possible distinct arrangements. Focusing on the 15 basic pairings, we can set a = x + i_a, b = x + i_b, and so on, where {i_a, i_f, i_b, i_e, i_c, i_b} is some permutation of {0,1,2,3,4,5}. Due to the symmetry of the three pairs, we can without loss of generality assume i_a < i_f, i_b < i_e, i_c < i_d, and i_a < i_b < i_c. We will denote each of the 15 pairings by a string satisfying these conditions, as shown below.

The other 15 volumes can be given by transposing the first two characters in each of these strings. However, many of these thirty possibilities are essentially redundant for purposes of generating volumes for six consecutive integers. For example, the first case is 012345, which signifies the assignments a=x, f=x+1, b=x+2, e=x+3, c=x+4, d=x+5.  Making these substitutions in the volume formula, we get

and if we transpose a and f we get

From a Diophantine standpoint, these two polynomials are not really distinct, because if we simply replace x in the first polynomial with –x-5, we get the second polynomial. Thus an integer solution of one maps directly to an integer solution of the other, so it suffices to consider the (signed) integer solutions of only one of them. This redundancy applies to each of the seven pairing cases 012345, 041523, 051234, 021435, 031425, 051324, and 051423. Furthermore, for the remaining eight pairings, transposing the first two characters of one leads to a polynomial that is given by substituting –x-5 for x in the polynomial for one of the other pairings, and vice versa. The pairings that are related in this way are (021345, 012435), (031245, 012534), (041235, 021534), and (041325, 031524). Therefore, it suffices to consider the signed integer solutions of just the polynomials based on the 15 pairings tabulated above.

Many of these can be ruled out immediately based on simple congruence considerations. Specifically, the polynomials based on the eight pairings listed below give values congruent to 2 modulo 3 for any integer argument, so they cannot give square values (since every square integer is congruent to 1 modulo 3).

Likewise the polynomials based on the three pairings 021435, 031524, and 051423 give values congruent to 3 modulo 4 for any integer argument, so they cannot give square values (since every square integer is congruent to 1 modulo 4). This leaves only four polynomials to consider, those based on the pairings 012534, 031245, 031425, and 051423. The polynomials are

Only the first of these polynomials is known to take on a positive square value for an integer argument, namely, with x = 6. This gives the original example of six consecutive integer edge lengths for a tetrahedron with volume 48. No other integer solution is known. However, if we relax the requirement for the edge lengths to be consecutive integers, and simply require them to be integers in arithmetic progression, we need only find a rational value of x for which one of these polynomials gives a rational square. Strictly speaking this gives us a sequence of rational edge lengths differing by 1, but we can clear the fractions and get a sequence of integers in arithmetic progression. Our best chance of finding such a solution is based on P₀₃₁₄₂₅, first because it has a square factor, so we can focus on just making a quartic equal to a square, and second because it has a known rational solution, from which we can attempt to construct another.

Since P₀₃₁₄₂₅(6) is a square, it is advantageous to write the quartic factor of this polynomial in terms of a new variable y = x – 6, which will have a square value when y = 0, meaning that the constant coefficient will be a square. Making the substitution x = y + 6, we get the quartic

We have f(0) = (72)², and we seek another rational value of y such that f(y) is a rational square. This is actually not difficult to do. First we construct another quartic that is the square of a quadratic polynomial and whose first three coefficients match those of f(y). Thus we consider a polynomial of the form

The first three coefficients match those of f(y) if we put A = 28 and B = 67/144. The complete polynomial is then

This is not generally the same as f(y), but they will have the same values for a certain value of y that makes their final two terms equal, i.e., we seek the value of y such that

The non-zero root of this equation is y = -911232/36983, which corresponds to a value of

We want edge lengths with positive values, so we can switch to the alternate equation given by replacing x with –x-5, which we already seen for this case gives the polynomial corresponding to transposing edges a and f. Thus defining z such that x = -z-5 we have

For this polynomial the argument z = -11 gives the value 144(48)², which was the original solution. The new solution, corresponding to the rational x value noted above, is

which gives the value

Thus the quantity in the parentheses on the right side is the rational volume of a tetrahedron with edge lengths

Each term of the polynomial consists of three squared edge lengths, so the common denominator is (36983)⁶, which is also the denominator of the squared volume. Therefore, multiplying through by this factor, we get a tetrahedron with integer edge lengths in arithmetic progression

and the volume of this tetrahedron has the integer value V = 23526783340621392. A diagram of this tetrahedron, indicating the arrangement of edge lengths, is shown below.

Using this solution, the process can be repeated to find another solution, and so on. Hence there are infinitely many such solutions, albeit extremely large.

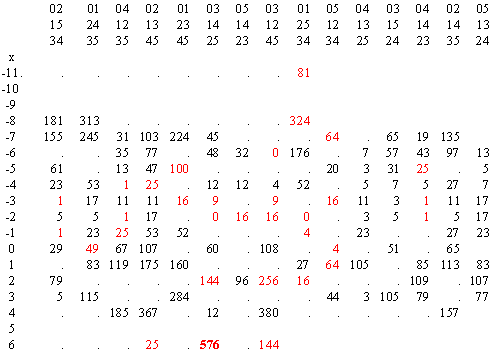
Incidentally, although the 15 polynomials for volumes of tetrahedra with consecutive integer edge lengths never (with just one known exception) yield positive square integers, their values in the negative range usually do have square magnitudes. Since the polynomials are of 6th degree, they go to positive infinity in each direction, so they are negative only over a very limited range, but within this range the values usually have square magnitudes. The table below shows the square roots of all the (known) square integer magnitudes of each of the 15 polynomials.

Among these magnitudes, only the value at x = 6 for the polynomial 031425 is positive, representing the only known case of consecutive integer edge lengths (6 through 11) giving an integer volume. The values highlighted in red are themselves squares, meaning that the magnitude of the polynomial is actually a 4th power.

Geometrically, the significance of a negative value for the squared volume of the tetrahedron with a given set of edge lengths is that those edge lengths do not satisfy all the triangle inequalities, so it isn’t actually possible (in real space) to connect them. Since the polynomials we are considering represent sets of edge lengths consisting of 6 consecutive integers, it is expected that the only negative values of the square volume would be for x values near zero, because for sets of consecutive integers far from zero, the ratios of the edge lengths approach 1, and we are assured of satisfying the triangle inequalities.

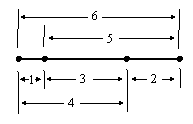
The above table shows three cases where the squared volume is zero, which signifies that the edge vectors are not linearly independent, i.e., they all lie in a proper sub-space, either a plane or a single line. Two of these cases are for integer sequences that pass through zero, so they don’t represent consecutive integer magnitudes. Only one case, with the argument x = -6 for the polynomial 031245, actually gives zero volume for consecutive integer edge lengths. Strictly speaking, this is for the negative edge lengths -6, -5, -4, -3, -2, -1, but since these lengths only appear squared in the volume formula, we know that the lengths 1, 2, 3, 4, 5, 6 will give the same result, provided we note that the arrangement is affected by this transformation. Essentially we must take the “complement” of the indices, so the arrangement 031245 becomes 524310, which we can re-arrange into our conventional format (with the pairs in order of magnitude, and the indices within each pair in order of magnitude) as 012534. We would then replace x with –x-5 in this polynomial to give the applicable volume polynomial for the edge lengths 1, 2, 3, 4, 5, 6. As expected, we find that this arrangements of edges is degenerate – in fact, all the vertices and edges are co-linear, as can be seen in the figure below.

It’s interesting that although the quartic factor of P₀₃₁₄₂₅(6) is irreducible, it differs by a square from a polynomial that splits completely into linear factors, i.e., we have

If the quartic is the square of some integer m, we have

The only known integer solution is the degenerate case x = 0 with m = 72. As described above, we can find infinitely many rational solutions of this equation (leading to tetrahedra with integer volumes and edge lengths in arithmetic progression), but it seems very difficult to find another integer solution, besides x = 0, or to prove that no other integer solution exists.

Return to MathPages Main Menu