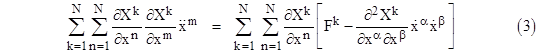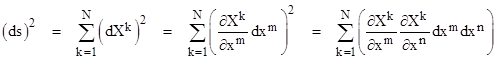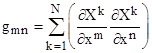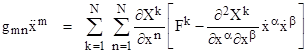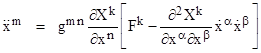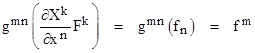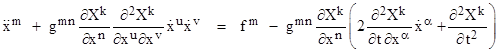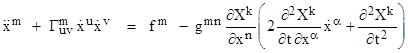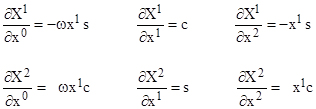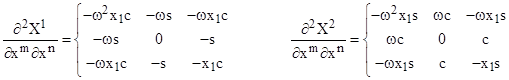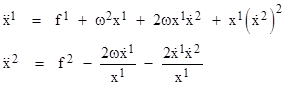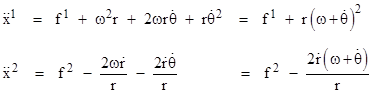Curved Coordinate Systems and Fictitious Forces

Aristotle argued that the idea of motion in a vacuum is unintelligible, because he regarded position as the fundamental attribute of an object’s state, and any change in the state of an object requires a “force” – essentially by definition. Thus to explain why a stone continues to move after it has left the hand of the thrower, Aristotle claimed that the air surrounding the stone continued to exert a force that tended to perpetuate its motion. The precise details of how the air performed this feat were not clear, but the general idea can be gathered from Aristotle’s use of the term antiperistasis, by which he evidently meant “mutual replacement”. The implication is that the primary force of the thrower’s hand not only causes a movement of the stone, but also sets the air into some kind of vortex motion, with the air in front of the stone being pushed aside, and this displaced air forces the surrounding air to fill in behind the stone and urge it forward, as depicted in the figure below.

Thus the object and its interaction with the surrounding medium generates a self-perpetuating motion. In essence, the object pushes on itself, as the forward force with which the object displaces the medium in front is communicated by the medium to the rear of the object. Aristotle argued that this was not quite a “perpetual motion machine”, because the vortex would gradually dissipate and hence the stone would eventually return to rest. We may be inclined to smile at this explanation for the persistence of motion, but it really is not so different from the modern concept of inertia, except that the latter dispenses with the mechanistic medium, and simply asserts that the object pushes on itself directly, i.e., that objects maintain their motion by the “force of inertia”. Of course, we regard the “force of inertia” as a fictitious force, but the distinction between real and fictitious forces is less meaningful than is sometimes claimed.

The beginnings of the modern concept of inertia can be found in the writings of several scholars in the middle ages. For example, Buridan developed the impetus theory, according to which a force is imparted to an object when it is thrown, and this force continues to travel with the object, maintaining its motion, until the force is dissipated. This theory simply replaces Aristotle’s “mutual replacement” mechanism with the bare assertion that material objects themselves can carry active force. At this stage, position was still regarded as the primary state attribute, so any motion still required a “real” force.

The last step on the way to the modern idea of inertia was taken by Galileo, Descartes, Huygens, Gassendi, Newton, and others, when they decided that a certain class of motions could be regarded as primary states in themselves. This was the origin of the classical principle of relativity, which was largely motivated by the efforts to account for the undetectability of the Earth’s motion in the Copernican model. However, the idea of inertia also owed something to the metaphysical notions about circles and circular motion as ideal states. Even Galileo, often called the founder of the modern doctrine of inertia, believed to the end of his life that circular motion (such as that of astronomical bodies) could be a natural state that needed no force to sustain it. But others soon focused on rectilinear motion at constant speed as the only true “states of motion”, i.e., states that would persist indefinitely until some “real” force is applied to bring about a change in the state of motion. In this way, the real force thought necessary by Aristotle and Buridan to account for the persistence of motion was essentially defined out of existence... leaving nothing but the unadorned persistence of motion.

At exactly the same time that the modern concept of inertia was established, ridding physicists of the need for a force to explain what keeps ballistic objects in persistent motion, Newton introduced a new force, the universal force of gravity, to explain what keeps the moon and planets in their persistently curved motions. This was initially seen as an occult pseudo-force by many of Newton’s contemporaries. Just as with Aristotle’s attempt to give a mechanistic explanation for the force of inertia, there were many attempts to give mechanistic explanations for the newly recognized force of gravity. In fact, Huygens tried to explain gravity in terms of a vortex of some ethereal substance moving rapidly around the Earth (and presumably around all other bodies). As with Aristotle’s vortex, the detailed functioning of Huygens’ model was never entirely clear, but in general Huygens claimed that the vortex was somehow constrained to within a certain limited region, and the centrifugal force of the vortex would cause the material to be more dense in the outer regions. The resulting gradient would then tend to force inwards any objects that were not participating in the vortex motion. One might think of it as a force of buoyancy, since the rotating material was effectively “heavier” (in the outward direction) than any non-rotating material. Oddly enough, in later editions of the Principia, Newton himself speculated on a possible aether being less dense near large bodies, resulting in a pressure gradient to account for the force of gravity. However, the difficulties with such schemes are obvious, and none of them ever gained general acceptance.

It’s ironic, though, that Huygens’ model sought to combine circular motion and the two mysterious “pseudo-forces” (inertia and gravity) in a single theory. Recall that centrifugal force is an inertial force (also known as a fictitious force) in the Newtonian sense, because according to Newton the tendency of an object to persist in its present “state of motion” (i.e., its present speed and direction) requires no force. Only changes from one state of motion to another require (and manifest) the action of a force. Hence the aether in Huygens’ model was not actually subject to a centrifugal (outward) force, it was subject only to a centripetal (inward) force, which accelerated the aether by continually changing its direction, moving it in a circle around the earth. From this point of view, the real motive force in Huygens’ model was whatever centripetal force was compelling the aether to remain confined to the region around the earth. Clearly Huygens could not appeal to any direct force of attraction to the earth, because that force of attraction is precisely what he was trying to explain with his vortex. In Descartes’ theory, the earth’s vortex extended out until it was confined by the vortices surrounding other bodies. Unfortunately this implies that the large gravitating bodies actually repel each other, unless we imagine a hierarchy of bodies and vortices of different strengths. But clearly such theories have so many problems that we can’t be surprised by the eventual acceptance of the Newton/Cotes interpretation of gravity as a primary force, innate to matter (notwithstanding Newton’s famous disavowal of this interpretation in a letter to Bentley). It’s also ironic that although Huygens, Leibnitz, and many others were unwilling to accept gravity as an innate force with no need of mechanical explanation, they had accustomed themselves to accepting the equally (if not more) mysterious innate force of inertia, dispensing with the mechanisms that earlier generations of scientists had considered necessary for intelligibility.

An even greater irony is the fact that, just as inertial forces were declared to be fictitious based on the classical principle of relativity, the “force of gravity” was likewise declared to be fictitious with the advent of general relativity. According to Einstein’s theory, the motion of the moon around the earth (for example) is indeed inertial motion, just as Galileo had wrongly (or, as it turns out, rightly) believed. With each new theory of relativity, the meaning and significance of space and time coordinate systems was profoundly changed, and the concept of “force” became more ambiguous. Despite the fictitious nature of gravity, we still normally deal with it as a force, and in fact we often still deal with inertial forces (such as centrifugal and Coriolis forces) as real forces.

Another source of ambiguity and confusion regarding concepts such as “centrifugal force” has been the lack of agreement as to how they should even be defined. Often no explicit definition is given, and an author will simply describe a scenario involving some kind of rotation and then state that something in that scenario is sometimes called “centrifugal force”. Thus the term is introduced merely by an example, rather than by a formal definition. Even when a definition is provided, one often finds the term being used in a different sense just a few pages later. For example, many texts define “centrifugal force” as the reaction force that a swerving object exerts on whatever is constraining it to follow its curved path. This of course if a real (Newtonian) force, but shortly thereafter the same texts will talk about the centrifugal force experienced by the swerving object itself, even though this is a fictitious force (in the Newtonian sense). Newton himself, in the Principia, uses the term “centrifugal force” in three different ways.

But the confusion over whether to apply the term “centrifugal force” to a real reaction force or only to direct fictitious forces is less interesting than the ambiguity in the definition of fictitious forces themselves. They are defined as acceleration components appearing in the equations of motion of a particle when those equations are expressed in terms of a non-inertial coordinate system. To see how these extra components arise, we start with the familiar form of Newton’s basic law of motion for a particle of mass m, in component form, using dots to signify derivatives with respect to time

where F is the applied force per unit mass, and superscripts denote indices (not exponents). This equation, as it stands, is valid only for a restricted set of space and time coordinate systems (X,t). Specifically, it is valid only if (X,t) constitute an inertial coordinate system, defined (circularly) as a system of coordinates in terms of which Newton’s laws of motion are valid. The space coordinate axes must be rectilinear and orthogonal, and the space coordinates of any particle not subject to forces must be linear functions of the time coordinate. Also, to every action there is an equal and opposite re-action. Now, if we assume that at least one such coordinate system exists, in what other coordinate systems would (1) be valid? If (1) is not valid for a certain coordinate system, how must it be modified to make it valid?

Let X¹, X², …, X^N and t = X⁰ denote a system of space and time coordinates (in N space dimensions) such that (1) is valid, and suppose we express those space coordinates as functions of another set of coordinates x¹, x², …, x^N, and t = x⁰ as follows

In Galilean spacetime we have X⁰ = x⁰ = t. Now, to express the right hand side of equation (1) in terms of the x coordinates, we need to differentiate X^w twice with respect to time. The first differentiation yields

where summation from 0 to N is implied over any repeated Greek indices in any single term. Differentiating again with respect to t, we get

Of course, the second derivative of t with respect to t is zero, but we include that term so as to maintain a consistent range for the Greek indices. We can now multiply through by ∂x^σ/∂X^ω to give

The left hand expression is simply the original acceleration, and hence the specific force F^σ, transformed to the x coordinate basis. We denote this transformed force as f ^σ. Also, the first term on the right hand side can be simplified by making use of the identities

Thus we have Newton’s law in terms of the arbitrary coordinates

The coefficients of the quadratic terms are commonly referred to as Christoffel symbols (of the second kind), and they comprise the components of the “affine connection”. These terms represent accelerations, but they can also be brought over to the left side of the equation and treated as a fictitious force , i.e., we can write

The familiar centrifugal and Coriolis forces are examples of such fictitious force components, but in general there are components corresponding to non-linear space coordinates as well as non-linear time coordinates. Of course, some terms in the above expressions are identically zero, because we assume the trivial mapping of the time coordinate in Galilean spacetime. To isolate just the non-trivial terms, we would write equation (2) as

Here we adopt the convention that Latin indices such as k and m range from 1 to N, and this applies to the implicit summations over such indices as well. We exclude the 0 index because the second derivative of x⁰ with respect to time is identically zero. Now, to solve these equations for the second derivatives of the x coordinates explicitly, we multiply through each term by ∂X^k/∂xⁿ with summation over n = 1 to N, and then we sum the resulting equations over k = 1 to N. Re-arranging the terms, and replacing the second derivative of X with F by equation (1), this gives

Now we make use of the Euclidean spatial metric for the original coordinates

This shows that the line element in terms of the x coordinates can be expressed in the form

with the implied summations from 1 to N, where the g_mn represent the components of the covariant metric tensor, given by

Substituting into equation (3), we get

Multiplying through by the contravariant metric g^mn, and omitting the summation symbols on the right side (since the indices now appear twice in each term), this gives

The first term is the contravariant force with respect to the x coordinates, i.e.,

Thus we can write the equations of motion as

From this we can see that Newton’s law in the original form of equation (1) is also applicable with respect to the x coordinate system if and only if the X coordinates are all linear functions of the x and t coordinates (and vice versa). If the transformation is non-linear, we must include the terms represented by the second term on the right side of the above equation. The coefficient of those terms would be simply the Christoffel symbols, except for the fact that the indices don’t all extend over the same range. The Latin indices k and n are summed from 1 to N, but the Greek indices α and β are summed from 0 to N. We could have made all the indices sum from 0 to N, but in that case the metric tensor would have been singular (because the time coordinate doesn’t appear in the classical line element for distances), and hence it is not invertible.

We may now consider the question of what to call the extra terms in the equation of motion when expressed in terms of a “non-linear” coordinate system (i.e., a system that is not linearly related to an inertial coordinate system). The naming is inconsequential, but it is sometimes of interest to clarify the meaning of fictitious forces. We might simply regard all of the extra terms as fictitious forces, and thereby maintain the exact form of equation (1). At the opposite extreme, we could regard all those terms as corrections to the acceleration for these coordinates. In that case we wouldn’t maintain the exact form of equation (1), although by the introduction of these “fictitious accelerations” we could still claim that the specific force (per unit mass) equals the total “acceleration”.

An intermediate alternative is often adopted. The terms representing the effects of non-linear space coordinates are brought over to the left, where they can then be expressed in terms of the Christoffel symbols, whereas the terms representing the effects of non-linear time coordinates are kept on the right side of the equation, and are called “fictitious forces”. This results in the equation of motion written in the form

Now we observe that the coefficient of the second term on the left can be written in terms of the derivatives of the metric tensor as follows

which are the Christoffel symbols of the first kind. Multiplying this by g^mn gives the Christoffel symbol of the second kind, denoted by Γ^m_uv. Thus we have

We recognize the vanishing of the left hand side as the condition for geodesic curves in the space (at any given instant). The second term on the left hand side is regarded as simply a correction to the acceleration to account for the non-linearity of the space coordinates, whereas the last terms on the right hand side are regarded (in this interpretation) as fictitious forces. The first term inside the parentheses is often called Coriolis force, and the second is often called centrifugal force. But it should be emphasized that there is no very compelling reason to split up the inertial forces in this way, bringing some over to the acceleration side and leaving others (those that involve time derivatives) on the “force” side of the equation. All of the terms represent the effects of non-linear transformation from inertial coordinates, and all of them can be accommodated by treating them as either fictitious accelerations or as fictitious forces.

This ambiguity should not be surprising, considering that force and acceleration are so closely identified in Newtonian mechanics, as shown by equation (1). In general relativity all four of the coordinates (three of space and one of time) are treated on a more equal footing, and the metric of spacetime involves all four, so we can bring all the terms over to the left side and consolidate them into the Christoffel symbol (with indices ranging from 0 to N). Indeed, when this is done, and when the metric coefficients are treated as potentials of the gravitational field, we find that Newton’s universal force of gravity disappears (just as did Aristotle’s force of persistent motion), and the motion of free particles in a gravitational field is regarded as purely inertial motion.

To illustrate the arbitrariness of the various ways of partitioning and labeling the terms arising from the use of non-Newtonian coordinate systems, consider the simple case of a particle moving in two (space) dimensions, and let the x coordinates be related to the Newtonian X coordinates by the relations

Thus the x coordinates are ordinary polar coordinates rotating at the angular speed ω. The first partial derivatives of this transformation are

where “s” and “c” denote respectively the sine and cosine of x² + ωx⁰. The second partial derivatives are

Using the first partials, we find that the covariant and contravariant components of the (spatial) metric tensor are

Inserting these expressions into equation (4) and simplifying, we get the equations of motion in terms of the x coordinates

where

Thus the forces in the x² direction are scaled by x¹. Substituting the more familiar symbols r,θ for the coordinates x¹,x², the equations of motion are

Consider a particle moving in a circular path around the origin at the absolute angular speed Ω. If we describe the motion of this particle in terms of polar coordinates rotating at the speed ω = Ω, then dθ/dt = 0, and we could say that relative to this rotating coordinate system the particle is subject to the centrifugal force rΩ² and the (scaled) Coriolis force 2Ωdr/dt. On the other hand, if we describe the motion of this same particle in terms of stationary polar coordinates, i.e., with ω = 0, then we have dθ/dt = Ω in terms of these coordinates, and we still have the same terms rΩ² and 2Ωdr/dt added to the radial and angular force terms respectively. However, some might argue that these terms can no longer properly be called centrifugal and Coriolis forces, because Ω now signifies the angular speed of the particle rather than the angular speed of the coordinate system. According to many reference texts, centrifugal and Coriolis forces (and fictitious forces in general) arise only from accelerated motion of the coordinate system, not from curvature of the spatial coordinates. The present example shows that precisely the same “non-Newtonian” terms occur in both the rotating and the stationary polar coordinates, the only difference being that in one case the terms arise from the non-linearity of the space coordinates, whereas in the other they arise from non-linearity of the time coordinate. Claiming that the terms rΩ² and 2Ωdr/dt represent fictitious forces in one case and fictitious accelerations in the other is merely a matter of convention. We might borrow Aristotle’s term antiperistasis to describe the “mutual replacement” between these two concepts. Of course, we also have ambiguity between centrifugal and Coriolis components, since (for example) the term 2ωrdθ/dt in the first equation of motion could be seen as a kind of Coriolis effect or consolidated with the other terms into a single centrifugal term.

Return to MathPages Main Menu