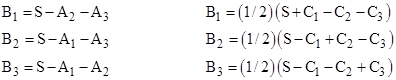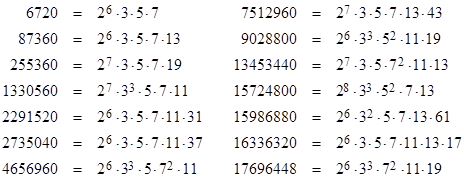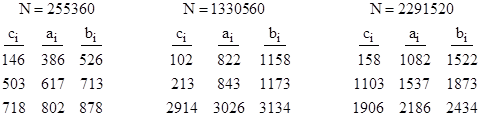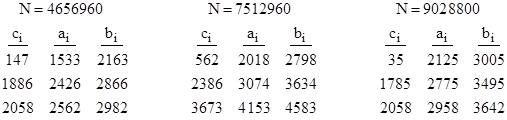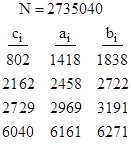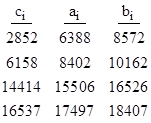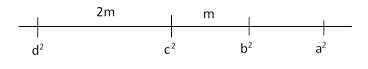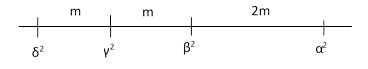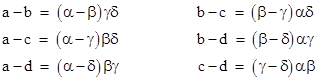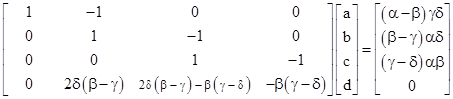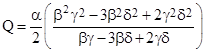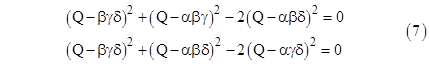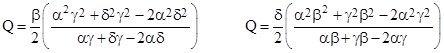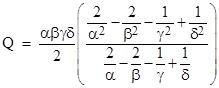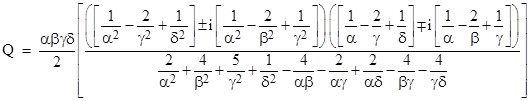The Amanda Arrangement

"I want an official Red Ryder, carbine action, two-hundred shot range model air rifle!"

"No, you'll shoot your eye out."

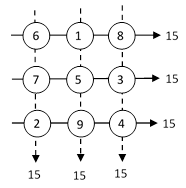
Consider a set of distinct numbers arranged in some geometrical pattern on the plane such that every sum of co-linear numbers through the pattern has the same value. The most common example is a magic square, which consists of a square arrangement of numbers such as the 3-by-3 arrangement shown below.

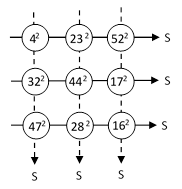
It’s customary to require the sums along each of the main diagonals to also equal the common sum, but even without those diagonals conditions we already get interesting structure from just the six orthogonal sums, especially if we impose some numerical constraints on the individual numbers. For example, we might seek a square arrangement of perfect square integers. The smallest such example is

where the common sum is S = 3249 = 57². As discussed in the note on Orthomagic Square of Squares, this is just one of an infinite family of such arrangements. (On the other hand, if we impose the diagonal conditions as well, there are no known 3x3 magic squares of squares.)

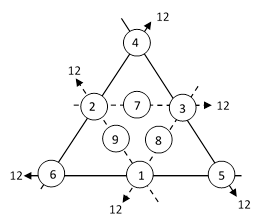
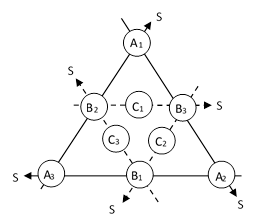
It’s interesting to consider other planar arrangements of nine numbers with six specified sums required to have the same value. One such pattern is the nested triangular arrangement – which we call an Amanda arrangement – as shown below.

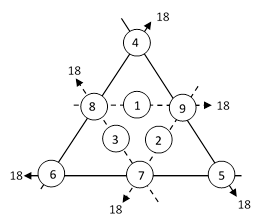
In this pattern each of the six indicated sums of co-linear terms is 12. Several interesting symmetries appear in this arrangement. Note, for example, that each of the pairs (1,7), (2,8), and (3,9) differ by 6, and if we transpose each of these pairs the net effect is to increase each of the six indicated sums by 6. (Each outer sum is incremented by +6, and each inner sum is incremented by +6–6+6.) Hence we have the “dual” arrangement

To show that every Amanda Arrangement has such a dual, let us assign symbols to the terms as shown in the figure below.

We have the following six equations in the nine variables

Each of these sets of three equations can be solved for the B terms as follows.

Subtracting A₁, A₂, and A₃ respectively from both sides of the three equations on the left, and subtracting C₁, C₂, and C₃ respectively from both sides of the three equations on the right, these equations can be written as

for j = 1, 2, 3, where for convenience we have defined the parameters

Thus the three differences B_j – A_j are all equal, as are the three differences B_j – C_j. The latter equalities are sufficient to ensure that each Amanda Arrangement has a dual of the kind described previously, i.e., transposing B_j and C_j. Furthermore, summing each of equations (1) over the index j gives

Subtracting S–α from both sides of the left hand equation, and subtracting S–γ from both sides of the right equation, we get

Substituting back into equation (1) gives

and hence

In our original example, each of the opposite pairs of the inner triangle differed by 6, and each of the opposite pairs of the outer triangle differed by 3. The above equation shows that this ratio of 2 applies to all Amanda arrangements. We also note that this equation is symmetrical in B_j and C_j, since it can be written in the form

Now suppose we require the individual numbers to be perfect squares. It isn’t obvious that any such arrangements exist, but in fact they do, although they are fairly rare. One way of seeking such arrangements is to examine the positive integers in sequence, and for each integer N determine the two-part factorizations N = xy where x and y are integers with the same parity and with x greater than y. Then for each such factorization compute b = (x+y)/2 and c = (x–y)/2, so we have N = b² – c². If an integer N has three distinct factorizations such that a² = (b² + c²)/2 is a square integer, then these numbers represent an Amanda arrangement of squares, putting A_j = a_j², B_j = b_j², and C_j = c_j².

For example, the integer N = 6720 has (among others) the three factorizations

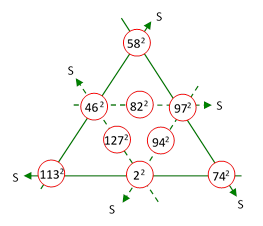
The first of these factorizations gives b = (224+30)/2 = 127 and c = (224–30)/2 = 97, and we find that 127² + 97² = 2(113²), so a = 113. Likewise the other two factorizations listed above give integer values of a, so we have found the smallest Amanda arrangement of squares shown below.

The common sum for this arrangement is S = 18249, whereas for the dual arrangement (found by transposing the inner opposite pairs) is S′ = 24969.  The difference between these two common sums is 6720 = (2⁶)(3)(5)(7), which as we’ve seen is also the common difference between the opposite numbers for the inner triangle. Of course, multiplying all the base numbers by a constant trivially gives another Amanda arrangement of squares, as does rotating the numbers by 120 degrees or reflecting about a suitable axis, but the results are not essentially different from this one or its dual.

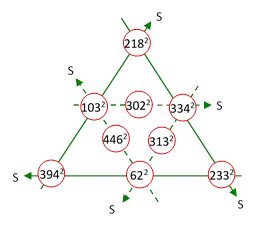
The next smallest primitive Amanda arrangement of squares is based on the factors of N = 87350, leading to the arrangement shown below.

For this arrangement the common sum is S = 213369, and the common sum of the dual arrangement is S′ = 300729. As always, the difference between these two sums, which is the common difference between the opposite elements of the inner triangle, i.e., 87360.

Examining all the integers N less than ten million, we find that there are only nine “Amanda numbers”, i.e., numbers with three (or more) acceptable factorizations leading to Amanda arrangements. One of these numbers (N = 27350040) actually has four acceptable factorizations, so it serves as the basis of four distinct primitive Amanda arrangements. The fourteen Amanda numbers less than twenty million, along with their prime factorizations, are listed below.

Each of these is divisible by 2⁶. The arrangements corresponding to the first two of these Amanda numbers have already been depicted. The square roots of the vertex values for the arrangements corresponding to the next six values, excluding 2735040, are as follows:

The squares of the elements in each row of any of these 3x3 arrays are in arithmetic progressions (since c_i² + b_i² = 2a_i²), and the differences between the squares of the values in neighboring columns are the same for each row. This is reminiscent of the conditions on a 3x3 array of squares that would be necessary for a magic square of squares, since we can arrange the numbers in a 3x3 magic square so that each row and each column is an arithmetic progression. However, there are no (known) 3x3 magic squares of squares, whereas we have found these several examples of Amanda arrangements.

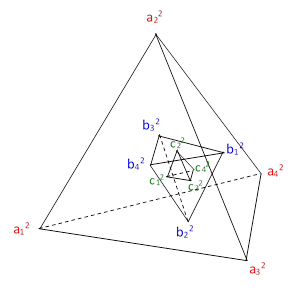
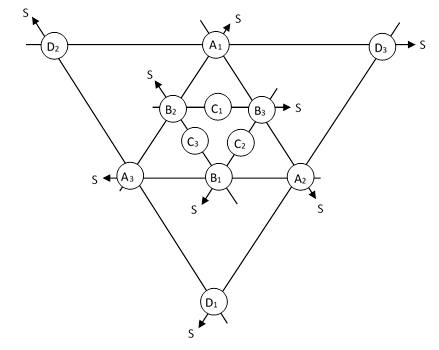
In the above tabulations we left out the case N = 2735040 because, as noted above, for that case there are four (rather than just three) acceptable factorizations. Hence we could construct four distinct Amanda arrangements from this number. However, it’s more natural to regard this as a three-dimensional tetrahedral arrangement, as depicted below, where the sum of the vertices on each of the indicated planes has the same value.

The values of the vertex bases for this tetrahedral arrangement are listed below.

The sum of the four vertices in each of the eight planes comprising the faces of the two outer tetrahedra equals S = 56192890. For example, we have

This is the only tetrahedral Amanda arrangement of squares with N less than twenty million. Presumably there are infinitely many such arrangements, but they are evidently fairly rare. Only one other number with four acceptable factorizations is known (see below), and no number with five or more acceptable factorizations is known.

Above 17 million there seems to be a large gap, and the next two smallest primitive Amanda numbers are over 50 million:

We also find a number that is a square multiple of a previous Amanda number, so it isn’t primitive, but the previous number has only three acceptable factorizations, whereas if we multiply it by 4 we get

which has four acceptable factorizations, leading to the tetrahedral vertices shown below.

The first three of these triples are just multiples of the original triples, but the fourth is new, so this gives a second tetrahedral Amanda arrangement.

Another way in which we might seek to extend these arrangements is by adding more triangular levels, as indicated in the figure below.

Any such arrangement would require the relations

However, it isn’t self-evident that there is even one solution of this pair of equations, let alone three. This is closely related to the problem of finding four squares in arithmetic progression, which is impossible, as shown in another note. But equations (3) imply a slightly different condition, namely, four squares that occupy four of five consecutive terms in arithmetic progression. Specifically, if we require each of the vertices to be a square integer, equations (3) for each index require integers a,b,c,d such that

It follows that c² is half-way between a² and d², and b² is half way between a² and c², as depicted below.

The smallest set of four such values is

If we examine the other two possible ways of distributing four numbers over five consecutive terms of an arithmetic progression, it can be shown that no solutions exist for the case when the unoccupied term is in the middle, but we do find a solution for the case when the unoccupied term is at the low end, as depicted below.

This corresponds to the equations

The smallest primitive solution of this pair of equations is

This solution is closely related to the previous one, as discussed in another note, where we discuss how to generate an infinite family of primitive solutions to (4) and (5). To explore some other aspects of the relationship between these two solutions, note that the expressions for the differences of the first solution in terms of the values of the second solution are as shown below.

Also, we can factor both sides of the relation c² – d² = 2(b² – c²) to give

Substituting for c–d and b–c and dividing through by α, we get

Combining this with the equations for a–b, b–c, and c–d, we get the four equations in four unknowns

Solving this system of equations gives

where

Inserting the values of the parameters for the only known solution (23,17,13,7), this gives Q = 5730. Of course, the four conditions leading to this result are not algebraic identities, they are just numerical coincidences, so (6) is not an algebraic solution of (4). It happens to be a solution if we set α, β, γ, δ to the values for the one known solution of (5). However, even if α, β, γ, δ satisfy (5), they still do not make (6) an algebraic solution. To identify the further condition that must be satisfied by α, β, γ, δ in order to make (6) a solution, we consider another approach to the above expression for Q, which is to simply postulate a solution of the form (6) and then substitute those expressions into (4) to give the following two equations for Q:

The algebraic solutions of these two equations, respectively, are

These two expressions for Q are not generally equal to each other for arbitrary choices of the parameters. On the other hand, if we solve for the single value of Q that makes the left-hand sides of (7) equal to each other, we get the expression for Q beneath equation (6), but this does not generally give solutions of the individual equations (7). Interestingly, if we set the sum (instead of the difference) between the left sides of (7) to zero (a condition that would also be satisfied by genuine solution of those equations), and solve for Q, we get the more symmetrical expression

If substitute this expression for Q into the left side of the first of equations (7) we find (not surprisingly) that it does not vanish identically, but if we replace each occurrence of α² with the equivalent 2β² – δ², and then replace each β² with the equivalent 2γ² – δ², we find that the resulting expression factors as

Thus we have a solution if and only if (α–δ) = 4(β–γ). Noting that equations (5) imply

it follows that an equivalent condition is

This happens to be satisfied by the one known solution of (5), namely, α = 23, β = 17, γ = 13, δ = 7, so this explains why we can generate a solution of (4) based on this solution of (5). In general, any solution of (5) that also satisfies (8) can be used to generate a solution of (4). Substituting for δ in equations (5) and adding the results, we find that β must equal 3α – 4γ, and if we make that substitution both equations reduce to

Multiplying through by 13 and completing the square, this can be written as

and hence 13α = 23γ. This shows that there are no other dual solution sets of equations (4) and (5) of the type described here.

There is, however, another interesting structural aspect of these relations. In the preceding discussion we made use of the roots of the difference between the squares of the left sides of equations (7), because we considered the sum and the difference of those quantities. It might seem that we could force both quantities to equal zero by setting the sum of their squares to zero. Solving the resulting quadratic in Q leads to the rational expression

This could be regarded as a an rational algebraic pseudo-solution, because for any arbitrary values of the parameters it makes the sum of the squares of the left sides of equations (7) vanish. The parameters need not even satisfy (5). If we were concerned only with real-valued numbers, this would indeed imply a complete solution, giving an infinite four-parameter rational algebraic solution of the pair of Diophantine equations (4). However, notice that this expression for Q is generally complex, so the vanishing of the sum of the squares of two quantities does not imply that each quantity individually vanishes. It so happens that Q has the purely real value 5730 for the parameter values of the single known solution, but for general parameters values we get a complex Q, and neither of equations (7) are individually satisfied. A complete solution requires values of the parameters that make Q real, and a sufficient condition for this to occur is for the parameters to satisfy (7) with α+δ = β+γ as noted previously.

Return to MathPages Main Menu