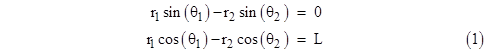On the Ellipse

An ellipse can be defined in several different ways. For example, it may be defined as a “section” (i.e., a planar slice) of a cone, from which we get the name “conic sections”. This is how the ellipse (and hyperbola and parabola) were originally defined by Menaechmus and later by Apollonius. Alternatively, an ellipse can be defined as a plane section of a cylinder (not surprisingly, since a cylinder is a limiting case of a cone). Both of these definitions involve constructions outside the plane of the conic. The most common modern definitions are those expressed entirely within the plane. For example, we can define an ellipse as the locus of points for which the ratio of the distance to a fixed point (the focus) and the distance to a fixed line (the directrix) is a constant less than 1. Similarly, we can define an ellipse as the locus of points for which the sum of the distances to two fixed points (the foci) is a constant.

Another characteristic property of an ellipse is that the rays from the foci to any point on the ellipse make equal angles with the tangent to the ellipse at that point. It follows that rays of light emanating from one focus of an ellipse will all be reflected off the interior surface of the ellipse and re-converge on the other focus. Indeed if we imagine an ellipsoid (the surface generated by rotating an ellipse about the axis connecting its foci), all the light emanating from a point-like source of light at one focus would converge on the other focus. Moreover, due to the fact that the sum of the distances from each point to the two foci is constant, it follows that the light would arrive in phase, because the optical path length of each of the rays would be identical. Presumably the light rays would pass right through the other focus (if nothing is there to intercept them), reflect off the ellipse again, and re-converge on the source, still perfectly in phase.

If we imagine ourselves located at one focus of a large ellipsoid with mirrored interior surface, a small ball located at the other focus would be visible to us at apparently the same distance in all directions. In effect, we would perceive ourselves to be at the center of a sphere whose interior surface was the exterior surface of the small ball at the other focus. In this sense, each focus of an ellipsoid totally “encloses” the other. It’s interesting to consider this scenario in terms of the retarded and advanced wave solutions of Maxwell’s equations, which are associated with outward and inward going wavefronts, respectively. In this elliptical chamber, each wavefront going from one focus to the other is both outward and inward.

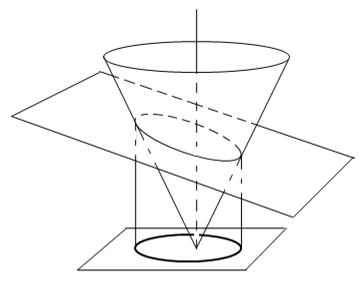
Considering how many different properties characterize an ellipse, rather than arbitrarily assuming one property as the defining property and then proving the others, it makes more sense to treat all the properties on an equal footing, and prove that they all go together. This can be efficiently done by examining a slightly different construction from all those noted above. Let us construct a curve by first slicing a right cone with a plane (in the manner of the ancient Greeks), and then projecting the intersection of these surfaces perpendicularly onto a plane normal to the axis of the cone. Note that the projection onto the normal plane distinguishes this construction from the original “conic section” definition of Menaechmus. This projective construction is illustrated in the figure below.

By symmetry, the locus of intersection between the cone and the plane is also the locus of intersection of two right cones with parallel axes offset from each other, as shown in the figure below.

We now select an arbitrary point on the locus of intersection, and consider a line drawn from the lower cone vertex to that point, and another line from that point to the upper cone vertex. Since both the cones are right cones with the same expansion angle α and parallel axes, it’s clear that the combined vertical height of those two line segments is H = sin(α)L₁ + sin(α)L₂, and likewise the sum of the projections of those line segments into the horizontal plane is S = cos(α)L₁ + cos(α)L₂. Hence, from the fact that H is the same, regardless of what point we select on the locus of intersection, it follows that the sum of projections on the horizontal plane is a constant S = H/tan(α). Thus the locus projected onto the horizontal plane consists of points such that the sum of the distances to the two axes is constant. In other words, it is an ellipse, and the points at which the cone axes intersect the horizontal plane are the foci.

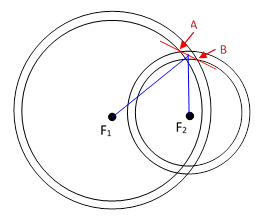
We can also see immediately that this locus has the “reflection” property. Viewing a region around the locus of intersection from directly above, we have the situation shown below.

The locus of intersection between the two cones necessarily lies on both of the cones, and they have the same expansion angle, so they have equal and opposite changes in radial distance with height. Hence the locus (shown in red) when progressing from point A to an incrementally nearby point B must increase the radial distance from F₁ by the same incremental amount that it decreases the incremental distance from F₂. (Of course, this also follows immediately from the constant sum of distances to the foci.) Now, since the base angles of an isosceles triangle are equal, it follows that the projected locus makes the same angle with respect to both of the circles, and therefore with respect to the two radials from the centers of those circles. This shows how closely related the “constant sum” property is to the “equal angle” property.

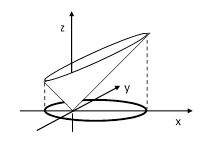
The algebraic approach to the ellipse is less elegant, but does reveal some interesting relationships. To express the conditions of an ellipse in algebraic form, consider a side-view of a sliced cone as shown below. (Both foci lie on the x axis, but only one is shown.)

Suppose a ray of length R emanating from the focus at the origin makes an angle α with the xy plane, and let θ denote the angle of the projected ray (on the xy plane) relative to the positive x axis. Then the coordinates of the endpoint of the ray are

For points on the sliced rim, the height z is a linear function of x, so we can write z in the form z = k₀ + k₁x for some constants k₀ and k₁. Thus we have

We also know that the length of the projected ray on the xy plane is r = Rcos(α), so we can solve the above equation for R and insert into the equation for r to give the polar form of the equation for an ellipse with the pole at one focus:

where

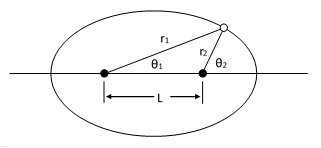
From this we can easily see that h is the “semi-latus rectum” and ε is the eccentricity, and how these relate to the major and minor radii of the ellipse. Now we consider a general ellipse in standard position, with rays from the foci to an arbitrary point as shown below.

Combining the fact that r₁ sin(θ₁) = r₂ sin(θ₂) with the basic polar equations, with the sign in the denominator reversed for the opposite foci, we have the relation between the angles

Clearing the fractions and re-arranging terms, we get

Thus recognizing that the quantity in the square brackets is sin(θ₁ + θ₂), we find that the eccentricity also represents this invariant function of the ray angles

A similar identity involving the sines of the rays angles can be inferred directly from the relations

Solving these equations for r₁ and r₂, we get

Therefore, the constant sum of the two radii divided by the distance between the foci is another invariant function of the angles

Now, in view of the identities

which come from the basic polar equation with θ = 0, we have

Multiplying this by the previous expression for ε, we get the general trigonometric identity, valid for any two angles θ₁ and θ₂,

We can also express, in algebraic terms, the previous geometrical proof of the reflection property. Taking the differential of equations (1), squaring, and summing the results, we get the metric line element for the base plane in terms of the two systems of polar coordinates

Since, for an ellipse, we have r₁ + r₂ = constant, it follows that dr₁ = –dr₂, and hence

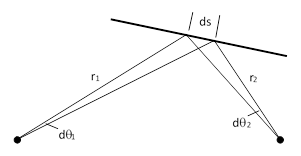
These quantities represent the projections of an incremental segment ds of the ellipse onto directions normal to the rays from the two foci, as shown below.

The small triangle with base ds is isosceles because r₁dθ₁ = r₂dθ₂, and so the base angle are equal, which (as before) implies that the radial rays make equal angles with the ellipse. Note that the areas swept out by the rays are half of r²dθ. Also, if we divide through the equation by dt we get the kinematic relation r₁ω₁ = r₂ω₂ where ω denote angular speed. Hence the areas swept out by the two rays per unit time are related by

We haven’t yet shown that the definition of an ellipse as the projected locus of the intersection of a plane and a right cone agrees with the original definition of the ancient Greeks, which regarded the intersection itself (in the slicing plane) as the locus. To show this, it’s convenient to give the general form of the equation of an ellipse in Cartesian coordinates. Placing the two foci on the x axis at the positions –q and q, and letting “a” denote half the major diameter, the constant sum of distances to an arbitrary point with coordinates x,y on the ellipse is

Letting u and v denote the quantities under the square root signs, we can square both sides and re-arrange terms to give

Squaring again, we get

which can be written as

Re-inserting the expressions for u and v, we get

Dividing through by 16 and collecting terms in x and y, this leads to

If we define “b” such that b² = a² – q², then clearly b is half the minor diameter. Hence we have the standard form of the equation for an ellipse in Cartesian coordinates with the origin at the center of the ellipse

Now we can see that projecting the conic section onto the base plane simply re-scales the lengths in the x direction, leaving the y direction unaffected, so we still have a locus of the same form, with a different value of “a”. The above derivation is reversible, so the resulting locus still satisfies the condition that the sum of the rays from the two foci is constant, from which all the other attributes of the ellipse follow.

Return to MathPages Main Menu