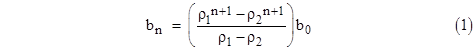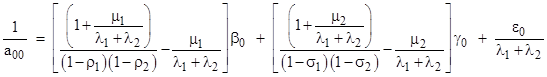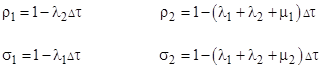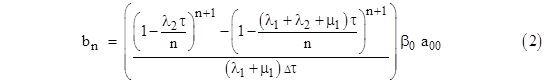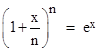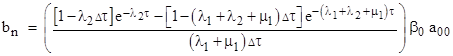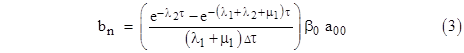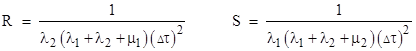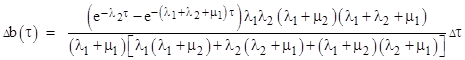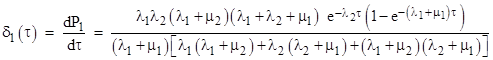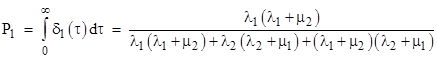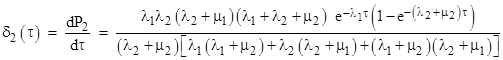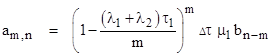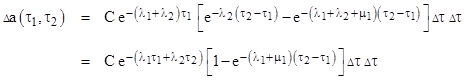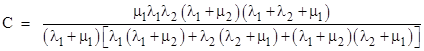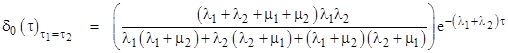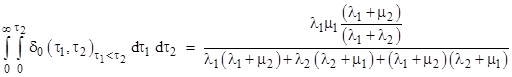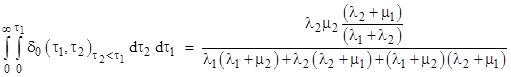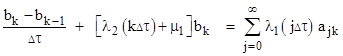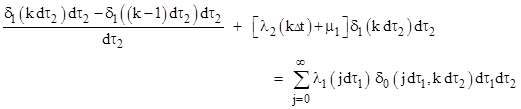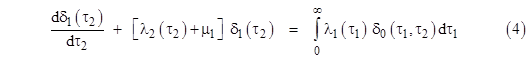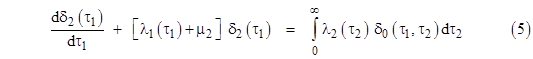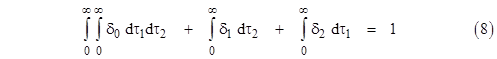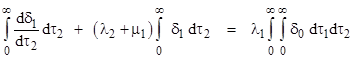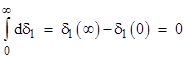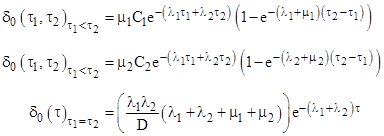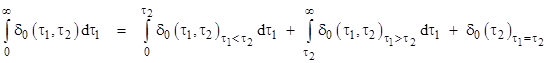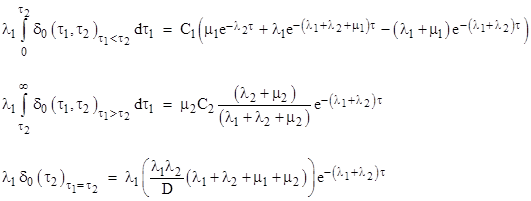Age Distributions in Continuous Markov Models

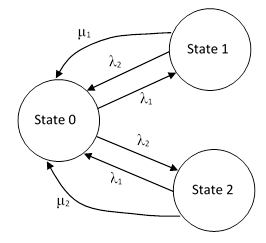
In another note we considered a generalized form of Markov models in which the transition rate parameters may be functions of the ages of the respective components. This was modeled in discrete time, and each state with n operational components consisted of an n-dimensional lattice space, with suitable aging transitions. In particular, we focused on a system with two components and three macro-states as shown below.

The transitions with rate parameters λ₁ and λ₂ leading back to State 0 result in the renewal of both components, whereas the transitions with rate parameters μ₁ and μ₂ represent repairs of just the single failed unit, while the unfailed unit is not renewed.

We denote by a_mn, b_n, and c_n the probabilities of the microstates in the macrostates 0, 1, and 2 respectively, with the understanding that the subscripts designate the (mean) age of the component(s) in a given microstate, measured in discrete units of the time increment Δτ. Although the original motivation for considering these age sub-spaces was to allow for the transition rate parameters to be functions of the ages of the components, we sought to demonstrate the soundness of such models by first considering the special case with all constant transition rate parameters. In terms of the nomenclature defined above, and putting θ = 1/ Δτ we found the following steady-state solution

where

We then defined the variables β_n = b_n/a₀₀ and γ₀ = c₀/a₀₀, and found that

and for brevity we have put

and

In these terms the value of a₀₀ was found to be given by

where

We now wish to determine the solution in the continuous limit, i.e., as the size of the time increments goes to zero. Thus for any given age τ = n Δτ we let Δτ goes to zero and n go to infinity. The characteristic roots go to

so equation (1) becomes

Recalling the limiting identity

we can express (2) for sufficiently small Δτ as

In the limit as Δτ goes to zero the quantities in the square brackets approach unity, so this can be written as

The other auxiliary parameters approach

and

Inserting these into the expressions for β₀ and γ₀, we get

Making these substitutions into the expression for a₀₀ (for sufficiently small Δτ), and simplifying, we get

Inserting these values of β₀ and a₀₀ into equation (3) and simplifying, we arrive at

The represents the incremental probability b for an incremental age range, so if we divide through by Δτ and convert to differentials, this gives the continuous density distribution for the ages of the components in State 1 of the model (at steady-state)

To check this, we can integrate this density for component ages ranging from t = 0 to infinity, which gives the total probability

This is consistent with the steady-state solution presented in the earlier note. By the same analysis we find that the density function for the component ages in State 2 is

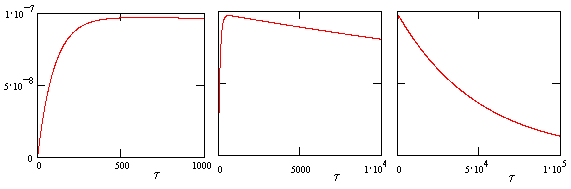
A plot of the age density for State 1 is shown below, based on the example specified in the earlier note, i.e., we have constant failure rate parameters of λ₁ = (50)10⁻⁶ per hour and λ₂ = (20)10⁻⁶ per hour, and repair rate parameters of μ₁ = 1/100 and μ₂ = 2/1000.

The density is zero at τ = 0, but increases rapidly to a maximum at about 400 hours, and on the larger scale the density decays approximately exponentially. Notice that, since States 1 and 2 have only a single operational component, they are represented by one-dimensional spaces. In contrast, State 0 has two operational components, so it is represented by a two-dimensional space. From the earlier note we have the relations

and we also know that consecutive values along any diagonal are reduced by the factor

Consequently we have

Replacing k+m with n, and choosing Δτ to be arbitrarily small, this leads to

Hence for arbitrarily small increments we have

Inserting the previous expression for Δb, we get for the result

where

The age density in State 0 with τ₂ greater than τ₁ is therefore

The symmetrical formula applies for the region where τ₁ is greater than τ₂. Note that both of these density functions vanish identically on the diagonal τ₁ = τ₂.

We must now consider the diagonal points in the State 0 space, i.e., the conditions for which τ₁ equals τ₂, which signifies that the components are of exactly the same age. It might seem as if this should not contribute any probability in the continuous limit, because the “area” of the diagonal in the age space is zero. Hence for any finite density it would contribute no probability. However, our expression for a₀₀ above contains only a single factor of  Δτ, so the density is infinite at that point, and hence at every point on the diagonal. It’s true that the probability contributed by each of those diagonal points is zero, but when we integrate along the entire diagonal we get a finite contribution. The discrete sum of diagonal terms is

so, inserting the previous expression for a₀₀, we find that the total probability along the continuous diagonal is

This shouldn’t be surprising, because the double-fault transitions return the system to the fully-renewed microstate (i.e., the microstate a₀₀), so there is always a significant portion of the population with both components of exactly the same age. The density along this singular diagonal is

To confirm these results we can integrate the expression for the age density of State 0 for the region with τ₁ less than τ₂ as follows

Similarly for the other region, i.e., with τ₂ less than τ₁, we get the integrated probability

Summing these two quantities and adding the contribution of the diagonal, we get (focusing on just the numerators, since they all have the same denominator)

Hence the sum of the three contributions equals the steady-state value of P₀ determined in the previous note. As an aside, note that the double integral of either one of the density distributions (for the region above or below the diagonal) evaluated over the entire space also equals the correct steady-state value of P₀, although apparently just by coincidence. This concordance applies not just to the integral over the entire age space of State 0, but even over each slice of constant τ₁ or τ₂, a fact which is significant for evaluating the continuous form of the age distribution equations.

Notice that the general case of equation (9) in the previous note can be expressed in the form

for any k greater than zero. (Boundary states are exceptions, because they lack one or the other of the aging transitions, but those will be treated appropriately when we sum these microstates to determine the probabilities of the macrostates.) To go over to the continuous case, we first define three density functions δ₀, δ₁, and δ₂ for microstates of incremental size by the following relations

Substituting these into the preceding equation (and noting that Δτ = dτ₁ = dτ₂) gives

Dividing through by dτ₂ and converting the summation to an integral, we get

By symmetry we also have the equation

Similarly, taking equations (8) from the previous note to the continuous limit gives

for  τ₁ , τ₂ > 0. The restriction to positive arguments is necessary due to the fact that equation (4) doesn’t apply for the singular boundary case δ₀(0,0). Note that the solution derived above satisfies these relations. The continuous limit of equations (9) of the previous note gives the governing equation for the age density function of State 0

and the preceding equations (6) give the boundary conditions for this equation in terms of the density functions of the single-fault states. By direct substitution of our previous solution for the age density of State 0 into this equation we can show that it satisfies the equation for every point other than the diagonal, where the function is discontinuous. The previous two equations, (4) and (5) relate the full-up and single-fault density functions, and together with the continuous gauge equation

they enable us to solve for the steady-state density functions for the three system states. Of course, the age densities are functions of time, so the overall probabilities for the three macrostates at any time t are

To show that the above equations reduce to the usual Markov model equations when the transition rate parameters λ₁ and λ₂ are constant, we can integrate equation (4) for τ₂ = 0 to infinity, giving the result

The first integral in this equation vanishes because

so we have the expected relation

which is the same as the first of the steady-state equations for the time-independent model. Likewise integrating equation (5) leads to the second of the steady-state time-independent equations. Of course, the gauge condition (8) reduces to P₀ + P₁ + P₂ = 1, so we have recovered all three of the steady-state equations with constant transition rate parameters.

It’s also interesting to see how our solution satisfies equation (4) directly, as opposed to the integral of equation (4). To show this, it’s convenient to define the constants

where

Then our solution for State 0 can be expressed as

and for States 1 and 2 we have

Now, by direct substitution and differentiation into (4) we find that the left hand side is

The right hand side of (4) is more difficult to evaluate, because the integration extends over all three of the regions of State 0. Thus the integral consists of the three terms

The third term on the right side might be surprising, since each point on the diagonal contributes zero probability. However, the terms of this equation are not probabilities, they are one-dimensional densities, and the diagonal contributes a positive density at each point. Evaluating each of these three terms, we get

The first two terms of the first integral equal the left side of equation (4), so all the remaining terms must sum to zero. Hence we must have

The constants C₁ and C₂ each have a factor of λ₁λ₂/D, so we can factor that out of all the terms, and we get (after canceling terms)

This does indeed equal zero, confirming that the solution satisfies equation (4). We also find that equation (4) is satisfied even if we evaluate the entire right hand integral (from zero to infinity) using just the δ₀ function that strictly applies only for τ₁ < τ₂.

Return to MathPages Main Menu