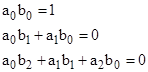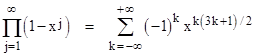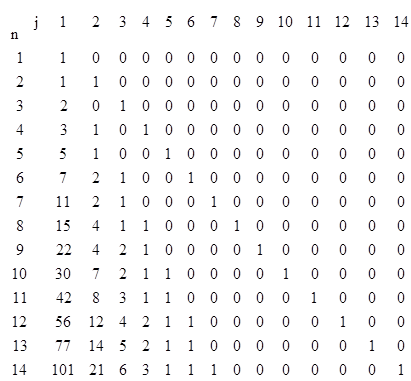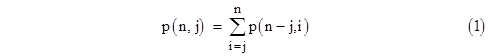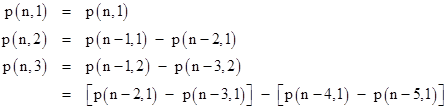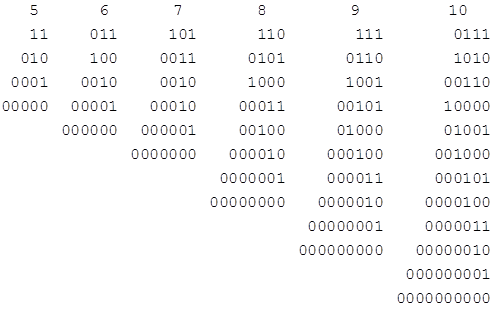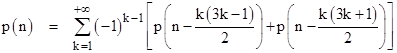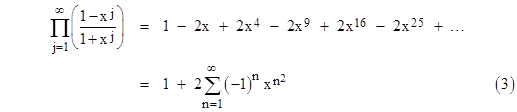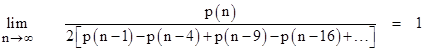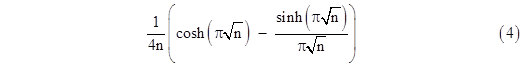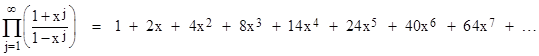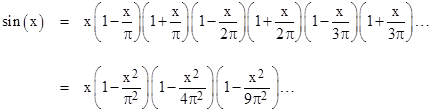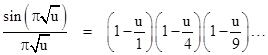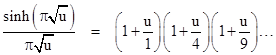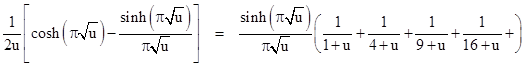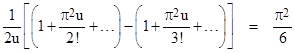On Euler’s Pentagonal Theorem

In September 1740 Euler received a letter from Philippe Naude asking (among other things) how to determine the number of ways in which a given positive integer can be expressed as a sum of positive integers. Within just a few weeks Euler replied with a description of the (now) well-known generating function for the partitions of an integer

and over the subsequent years he continued to derive and prove many fascinating results in this new branch of analysis, which he called partitio numerorum. One of his beautiful results in this area (indeed, in all of mathematics) is the proposition that, letting p(n) denote the partitions of n without regard to order, the values of p(n) satisfy the recurrence

where the numbers subtracted from n in each argument are the pentagonal numbers, i.e., numbers of the form (3k² + k)/2, where k ranges over all positive and negative integer values, and the sign of each term is (–1)^k+1. This was conjectured by Euler in 1741 based on numerical evidence, although he was unable to find a rigorous proof until 1750. He also noted that the coefficients of reciprocal power series are recurrence coefficients of each other, i.e., given two polynomials a(x) = a₀ + a₁x + … and b(x) = b₀ + b₁x + … such that a(x)b(x) = 1, we have

and so on. Therefore, the reciprocal of the generating function for p(n) is the generating function for the coefficients of the recurrence formula for p(n). In other words, the above recurrence for p(n) is equivalent to the algebraic fact that

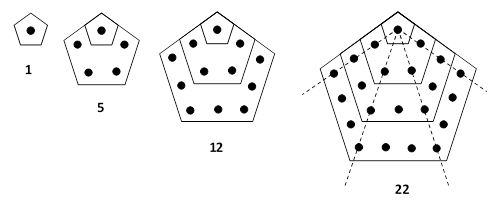
Euler discovered this by actually multiplying together all the binomial factors from (1–x) up to (1–x⁵¹). At intermediate stages of the calculation the coefficients of the various powers of x take on large values, but once all the factors have been applied and the terms have been consolidated, a huge amount of cancellation takes place, and every coefficient either vanishes or else equals +1 or –1. Moreover, the non-zero coefficients occur precisely when the power of x is a number of the form (3k²–k)/2. These were named “pentagonal numbers” by the ancient Greeks, because for positive values of k they arise from the pentagonal gnomons (after the Babylonian shadow clocks) as shown below.

Negative values of k give the series 2, 7, 15, 26, … Euler’s Pentagonal Theorem, which has certainly been re-discovered many times, is now seen as a special case of Jacobi’s Theorem on theta functions, but it’s still a striking result, and it’s interesting to consider various alternate ways of proving it, to get a better understanding of why it’s true.

One way of approaching the problem is to let p(n,j) denote the number of partitions of n with the smallest term j. Hence p(n) = p(n,1) + p(n,2) + … + p(n,n). Now we note that the partitions of n with smallest term of 1 can be formed by appending 1 to each of the partitions of n–1. Also, the partitions of n with smallest term 2 can be formed by appending 2 to each of the partitions of n–2 whose smallest terms are at least 2. Likewise the partitions of 3 can be formed by appending 3 to each of the partitions of n–3 whose smallest terms are at least 3, and so on. Of course, there is also one partition of n with smallest term n. This enables us to easily form the table shown below.

Except for the diagonal terms (i.e., the terms representing p(n,n) = 1), each entry in this array is given by the rules stated above, which can be summarized as

For example, the value of p(13,3) equals the sum of p(10,3), p(10,4), …, and p(10,10), which gives 2 + 1 + 1 + 0 + 0 + 0 + 0 + 1 = 5. Of course, if we add the term p(10,2) = 7 to this sum we get p(12,2) = 12, so we could just as well compute p(13,3) as p(12,2) – p(10,2). Thus in general we have

By applying this formula repeatedly we can express all the values on any row in terms of elements of the first column. Since p(n) = p(n+1,1), this allows us to determine a recurrence relation for the partition function itself. To illustrate for the first few elements, we have

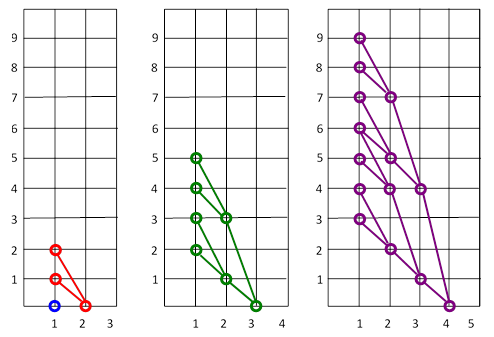
and so on. The value of p(n) will just be the sum of all these terms. We just need to determine the coefficients of each element from the first column. To do this, it’s helpful to consider the diagram below, which depicts the repeated applications of (2) to the elements of a given row.

Each element of the bottom row is the origin of a binary tree extending to the first column. On each step the vertical position can increase by 1 or by j, where j is the current column. The sign of the term remains the same when the vertical position increases by 1, whereas the sign is negated when the vertical position increases by j. It follows that the coefficient of each element of the first column is the sum of the term for each of the possible ways of reaching that element from the bottom row. For example, the term at the 4th row of the first column can be reached in two ways; we can begin in the 3rd column and increase by 1 on the first step and then 2 on the second step (the green path), or we can begin in the 4th column and increase by 1 on each step (the purple path).

In general, each row index can be expressed in the form

for some set of binary bits b₂, b₃, …, b_k, each of which is either 0 or 1. The number of terms in a representation equals one less than the starting column. A 0 bit signifies a summand of 1 (and no sign change), whereas a 1 bit signifies a summand of j with a reversal of sign. Hence the sign of the resulting contribution to the first column coefficient simply reflects the parity of the representation (odd number of 1s is negative). The values of the first several paths, along with their binary representations and signs, are listed below.

0 1+ 0000 4+

1 2– 0001 5–

00 2+ 0010 6–

01 3– 0011 7+

10 4– 0100 7–

11 5+ 0101 8+

000 3+ 0110 9+

001 4– 0111 10–

010 5– 1000 8–

011 6+ 1001 9+

100 6– 1010 10+

101 7+ 1011 11–

110 8+ 1100 11+

111 9– 1101 12–

1110 13–

1111 14+

This table doesn’t include the zeroth-order term, because the coefficient of p(n–1) is clearly +1. Now, there is only a single representation of 1 in this table, and it has a positive sign, so the coefficient of p(n–2) in the recurrence is also +1. There are two paths to “2”, one positive and one negative, so they cancel out, leaving a coefficient of 0 for p(n–3). Likewise, there are two representations of “3”, with opposite signs, so the coefficient of p(n–4) is also 0. However, there are three representations of “4”, two negative and one positive, so the coefficient of p(n–5) is –1.

Our objective is to understand why so much cancellation takes place, and why the non-zero coefficients are either +1 or –1, and why these occur only when the index is a pentagonal number (meaning that the row index in our nomenclature is one less than a pentagonal number). We first examine the representations leading to each of the first several row indices:

The key is to notice that most of these representations can be placed in pairs (with opposite parity) in a unique way. Any expression of the form x1 maps to the same number as 0x0, but with opposite parity, so whenever one of these appears, the other does also, and they cancel out. This pairing along is sufficient to eliminate a large fraction of the terms, but not all. It leaves unpaired only the representations of the form 1x0. However, any representation of the form 1x10 can be paired with 10x00, and again these have opposite parity so they cancel out. Thus we have covered all representations except those of the form 11x00, but we can cover some of these by noting that 11x100 maps to 110x000. Now we have covered all representations except those of the form 111x000, but we can continue to extend the mapping, and in this way we place each representation in a unique pair with another having the same value but opposite parity, so they cancel, except for those of the form 10, 100, 1100, 11000, 111000, 1110000, and so on. These are the only representations not covered by any of the infinite sequence of mappings, so the terms corresponding to these numbers will be the only ones with non-zero coefficients, and their coefficients will be either +1 or -1 (since each of these representations corresponds to a distinct number).

The sequence of representations 10, 1100, 111000, corresponds to 3+1=4, 5+4+2=11, 7+6+5+3=21, and so on. These can be expressed in the form

which is one less than the pentagonal numbers. Likewise the representations 100, 11000, 1110000, corresponds to 4+2, 6+5+3, 8+7+6+4, and so on. These can be written in the form

If we shift the indices by replacing n with n+1, this becomes

which again is one less than the pentagonal numbers, this being the other branch of those numbers. Consequently, we’ve proven that the partition function satisfies the recurrence

Incidentally, the representations of a number N in the form

can be placed in one-to-one correspondence with the partitions of N+1 into distinct parts. Given any representation of the above form, we can subtract 1 from each of the n–1 terms, and then add n, resulting in a unique partition of N+1 into distinct parts, and the number of distinct parts will equal one more than the number of 1s in the representation. Conversely, given any partition of N+1 into distinct parts, we can remove the largest summand m, and then add 1 to each of the other terms (so they now are distinct integers in the range 2 to m), and then express the result as an m–1 bit representation of N. Thus, letting O(n) and E(n) denote the partitions into an odd or an even number of distinct parts respectively, our previous discussion proves that E(n) – O(n) = 0 except when n = k(3k±1)/2, in which case E(n) – O(n) = (–1)^k. This is consistent with the fact that the product (1–x)(1–x²)(1–x³)… is the generating function for f(n) = E(n) – O(n).

Certain other sequences related to the partition function also have quadratic recurrence relations. Given any multi-set σ of positive integers, let h(σ) and g(σ) denote the number of elements and the number of distinct elements, respectively, and let s(σ) denote the sum of the elements of σ. Thus for the multi-set σ = {5, 3, 3, 2, 2, 2, 1, 1, 1, 1} we have h(σ) = 10, g(σ) = 4, and s(σ) = 21, and hence σ is a partition of 21. For any multi-set σ, we define the weight w(σ) as

Finally, let W(n) be defined as the sum of the weights of all the partitions of n. In other words, we define W(n) as

We find that W(n) = 0 for all non-square positive integers n, and W(n²) = 2(-1)ⁿ. To find the generating function for this series, we note that

The coefficient of xⁿ in the product of these functions for j = 1 to infinity is W(n), so we have

Since the product of the numerators is the reciprocal of the generating function for p(n), it follows that the summation on the right gives – asymptotically – a recurrence for the partition function. (If the denominator were a finite polynomial of degree d, the recurrence would be exact for d or more terms of the partition function, but since the denominator is an infinite series, the recurrence would be exact only for infinitely many terms.) In other words, we have

To illustrate, the value of p(34) = 10143 is approximated by twice the sum (with alternating signs) of the terms preceding it by 1, 4, 9, 16, and 25 in the sequence of p(n). This gives

The ratio of the true value to this approximate value is 0.997541… The errors of successive values alternate in sign and increase monotonically, as the ratio approaches 1.

Incidentally, the reciprocal of the series (3) was the subject of one of the propositions that Ramanujan mailed to G. H. Hardy in 1913, along with a letter of introduction:

DEAR SIR,

I beg to introduce myself to you as a clerk in the Accounts Department of the Port Trust Office at Madras on a salary of only £20 per annum. I am now about 23 years of age. I have had no University education but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at Mathematics. I have not trodden through the conventional regular course which is followed in a University course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general and the results I get are termed by the local mathematicians as 'startling'. . . . I would request you to go through the enclosed papers. Being poor, if you are convinced that there is anything of value I would like to have my theorems published. I have not given the actual investigations nor the expressions that I get but I have indicated the lines on which I proceed. Being inexperienced I would very highly value any advice you give me. Requesting to be excused for the trouble I give you.

I remain, Dear Sir, Yours truly,

S. RAMANUJAN.

It’s ironic that a man who is said to have been a personal friend of each integer should report his age as “about 23”. He was actually 25 when he wrote the letter, and he apparently feared that he would be considered “over the hill” if he admitted to being all of 25. One of the over one hundred mathematical propositions included with his letter was the assertion that the coefficient of xⁿ in the reciprocal of the series (3) is the nearest integer to

Hardy recalled his reaction when he first read the letter and some of the attached propositions:

It soon became obvious that Ramanujan must possess much more general theorems and was keeping a great deal up his sleeve… I had never seen anything in the least like them before. A single look at them is enough to show that they could only have been written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them.

The reciprocal of (3) is

Ramanujan was probably trying to make the proposition as “startling” as possible by expressing it in terms of the reciprocal series, without reference to the product form, since the product gives some hints for how one might go about proving this assertion, knowing all the roots and poles. Also, notice that (4) is simply the second derivative of cosh(πn^1/2)/π². To see why it’s natural to consider the square root of n as the argument for the trigonometric functions, recall Euler’s reasoning when trying to determine the sum of the inverse squares. Since the function sin(x) has the roots 0, ±1π, ±2π, ±3π, and so on, he reasoned (somewhat intuitively) that it may be legitimate to “factor” sin(x) into its linear terms as indicated below

Putting x = πu^1/2, this gives

Since sin(ix) = i sinh(x), we have the product for the hyperbolic sine

Differentiating both sides gives

In the limit as u goes to zero, the leading coefficient on the right hand side goes to 1, the quantity in parentheses on the right side goes to the sum of the inverse squares, and the quantity on the left side goes to

This shows how closely related Ramanujan’s proposition is to Euler’s famous summation of the inverse squares. This is also closely related to the number-theoretic function σ(n), the sum of the divisors of n, as discussed in the note on the average order of σ(n).

Return to MathPages Main Menu