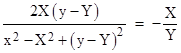Euclid’s Proposition III,20 and Its Converse

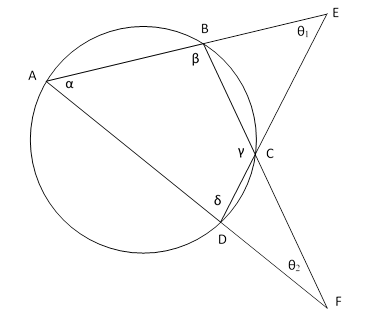
Some elementary propositions in plane geometry provide interesting illustrations of what might be regarded as a primitive form of gauge invariance. For example, suppose we are given four points A,B,C,D on a circle, and we are given the magnitudes of the angles θ₁ and θ₂ as shown below.

Specifying the values of θ₁ and θ₂ is not sufficient to determine the figure, not even up to rotational symmetry, but it is sufficient to determine the values of the quadrilateral angles α, β, γ, and δ. It’s a nice elementary exercise to work this out “from scratch”. First we have

Lemma 1: The sum of the interior angles of any triangle equals π.

Proof:  If we proceed along the edges, we make three turns for a total of 2π, meaning the average angle per turn is 2π/3, so the average interior angle of the turns is π/3, giving a total of π.

Now making use of this fact, it’s easy to show

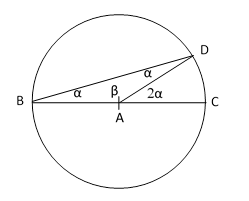
Lemma 2: The angle swept out by a chord of a circle with one end fixed equals half the angle of a central radius with the same moving end point.

Proof: As shown in the figure below, if the chord BD makes an angle α with the diameter BC, then by Lemma 1 the triangle ABD is isosceles with central angle π – 2α, and hence the complementary angle made by the radial line AD with AC is 2α.

This is the same as Proposition 20 in Book III of Euclid’s Elements (although Euclid didn’t prove it this way, and seems not to have considered the application to angles greater than π.) From this we immediately have the

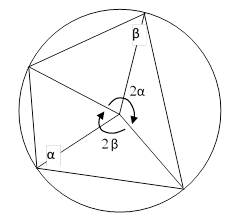
Corollary 2.1: The sum of two opposite angles of a quadrilateral inscribed in a circle is π

Proof: The chords making the two opposite angles of a quadrilateral meet at two points on the circle, and by Lemma 2 the central angles are twice the two quadrilateral angles, and these central angles precisely cover one whole revolution. Hence, if the two angles are α and β as shown in the figure below, we have 2α + 2β = 2π, and therefore α + β = π.

We used the fact that the sum of the angles of any triangle equals p (Lemma 1) to prove Lemma 2, but it’s worth noting that Lemma 2 can also be used to prove Lemma 1, since any triangle can be inscribed in some circle, and each interior angle of the triangle maps to a central angle twice as large, and these three central angles precisely cover one whole revolution. It might seems as if Lemma 1 is simpler and more fundamental than Lemma 2, but this perception is based partly on taking the circle and its properties for granted. We could, starting from a more primitive level, define a circle as a locus of points with the equi-angular property. In other words, given any triangle ABC, we could define a “circular arc” as a locus of points P such that the angle APC equals the angle ABC. This definition gives the ordinary circular arcs, although to prove this seems to be significantly more difficult than proving the converse.

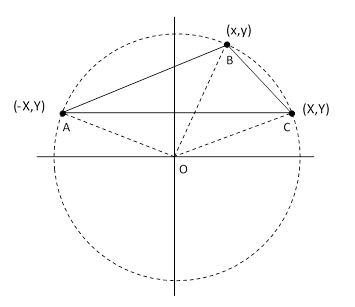
Given three points A,B,C on the plane, we can determine the point O that is equidistant from each of those three points, and without loss of generality we can arrange these points as shown below, scaled so the distances from O to each of the three points is 1. Let (–X,Y), (x,y), and (X,Y) denote the coordinates of the three points respectively.

We propose to move the point B in such a way that the angle ABC remains constant, and our claim is that this requires B to move along the perimeter of the circle. As shown previously, it is fairly trivial to prove that if B moves along the circle, the angle ABC remains constant, but now we are trying to prove the converse, which seems surprisingly difficult. The condition that the angle ABC is constant can be expressed algebraically in terms of the inverse tangent function as follows

Making use of the identity arctan(a) – arctan(b) = arctan((a–b)/(1+ab)), we can consolidate the terms on each side, and then take the tangent of each side, to give the relation

Clearing fractions, simplifying, and recalling that X² + Y² = 1, this gives x² + y² = 1, proving that the locus of points with constant angle is a circular arc. The subtlety of inferring the locus from the constant angle condition is basically due to the fact that the condition is singular at the anchor points, i.e., when (x,y) goes to either (X,Y) or (–X,Y). At those points the left hand side of the above relation goes to 0/0, so it is indeterminate. To continue the same circle on the other side of these points, we take the other root for Y, which reverses the sign on the right hand term in the above relation. This corresponds to a different “constant angle” than on the original arc. It would be interesting to express this proof in purely geometric terms, without making use of the arctangent function.

By proceeding from the converse proposition, we have not made use (at least not explicit use) of Lemmas 1 or 2, so it’s interesting to see if we can prove those by means of the converse proposition and the alternate definition of a “circle” as the equi-angular rather than equi-distant locus. We can actually prove Lemma 2 without Lemma 1, simply by observing that the ratio of a central to a perimeter angle on a given arc is the same as the ratio for those two angles on half the arc, as depicted below.

Whatever is the ratio of the angle AOC to the angle ABC, we can move B to the symmetrical position, and then it is clear that we have the same ratio of the half angles AOD and ABD. We could then move B to the new symmetrical position, and halve the angles again, and so on. Since we can do this for arbitrary angles, always preserving the same ratio of central to perimeter angle, it follows that every central angle is in this same ratio to the perimeter angle on the same arc. We know the ratio is two-to-one when AOC is a straight line, so every central angle is twice the corresponding perimeter angle. (Again, this is Euclid’s Proposition III,20.) With this we can now give a nice proof of Lemma 1, similar to Corollary 2.1. The sum of the interior angles of any triangle equals π simply because the central angles sum to 2π, as shown below.

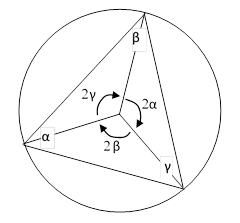
Returning to the original problem, with the four points A,B,C,D on a circle, we know the interior angles of each of the triangles ADE and ABF sum to π (by Lemma 1), and we also know that each pair of opposite angles of a quadrilateral inscribed in a circle sum to π (by Corollary 2.1), so we have

Solving these equations for α, β, γ, and δ gives

As noted previously, one of the interesting aspects of this problem is that the solution is fully determinate, even though the given information is not sufficient to fully specify the quadrilateral in the circle. This has something in common with, for example, the free gauge in the mathematical expressions for electromagnetic fields. The representation possesses “excess” structure, beyond what it needed to specify a given situation.

Incidentally, there’s an amusing story involving these propositions from the correspondence of Albert Einstein and his son Hans Albert during the first world war. At this time Einstein was working at the Kaiser Wilhelm Institute in Berlin, while his estranged wife Mileva was living in Switzerland with their two sons. Einstein carried on a rather strained correspondence with the elder boy, Hans Albert, often including math problems to challenge his son’s ingenuity. Posing math problems may not be the optimum way of establishing personal rapport with one’s child, but it seems to have been a genuine expression of the essentially intellectual and analytical nature of Einstein’s character. Hans Albert gamely tried to solve each puzzle sent to him, with mixed success. In November of 1917 Einstein included the following geometry problem in a letter to his (then) 13 year old son:

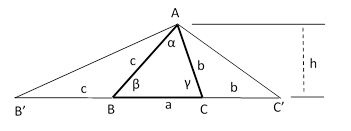
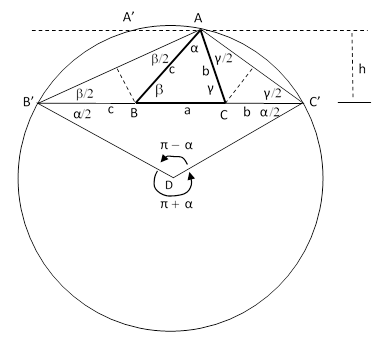
For a triangle ABC we are given the interior angle α at A, the height h of the point A (above the base BC), and the sum a + b + c of the edge lengths. From this information, construct the triangle.

Hans Albert made a start, but had to write back to his father admitting that he was unable to solve the problem completely. Now, since this was during the first world war, all the mail between Germany and Switzerland was examined by censors to be sure no war secrets were being revealed. (Einstein worked closely with Fritz Haber, who was developing chemical weapons for the German military, and Einstein himself did some military work as well, and he corresponded with scientists in many neutral and Allied countries, so it isn’t surprising that his international mail was carefully checked.) In his reply to Hans Albert on December 9, Einstein wrote

Your little letter pleased me very much… the postscript was the most amusing, though: it was not from you at all, but from the censor. He had provided the entirely correct solution to the problem I had posed for you in place of yours, and had written in pencil under your letter. It goes like this…

Apparently the military mail censors, at this critical juncture in the war, still had time to make extensive editorial comments on the mail they were reading. It’s amusing to think of the censor reading the puzzle, taking it up himself, solving it, and then not being able to resist adding his solution to the letter. The solution depended on “unfolding” the sides of the triangle to produce a line segment of the given length a + b + c, so we consider the general configuration shown below.

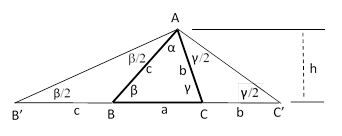
Since the flanking triangles are isosceles, we can easily fill in the angles as shown below.

Since α + β + γ = π, the angle B’AC’ is simply (α + π)/2, so our knowledge of α is sufficient to determine that angle. Apparently Hans Albert got this far, “but then [he] ran out of steam” as the censor put it. So far we have the line segment B’C’ of known length, and we know how far A is above that line, but we don’t know how A should be positioned horizontally. The censor realized that we have enough information to determine the circle that passes through the points B′, A, and C′, and the two places where this circle has the height h above the baseline are the two (symmetrical) possible locations of the point A, as shown below.

Notice that this construction relies on the fact that the (exterior) central angle B′DC′ is twice the perimeter angle B′AC. Thus, given α, h, and (a+b+c), we set out the line B′C′ of length (a+b+c), and then draw the lines B′D and C′D  making the angle α/2 with the line B′C′. Then draw the circle through the points B′ and C′ centered on the point D. The two points of intersection of this circle with a line located a distance h above B′C′ give equally suitable locations for the point A. The corresponding points B and C are then given by the intersections of the perpendicular bisectors (apothems) of the segments AB′ and AC′ with the line B′C′. As the meticulous censor concluded “In this way two triangles result [one based on A and the other based on A′], which you should also prove are congruent to each other”.

After describing the censor’s solution, Einstein’s letter to Hans Albert continued in a rather didactic tone:

I have sent you 5 very fine and interesting books for Christmas. This occupied me for an entire day, because the selection was difficult and, in addition, I needed an export permit from the military authority. They belong to you and Tete [Eduard Einstein, Hans Albert’s younger brother] together. I did not divide them between you. Reading and understanding is what is important, not possession.

It’s interesting how often Einstein reverted to that or similar expressions. Several times in his writings he summed up his view of life by alluding to “Lessing’s fine saying” that “the pursuit of knowledge is more precious than its possession”.

Return to MathPages Main Menu