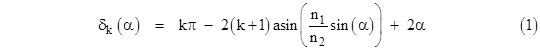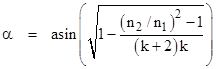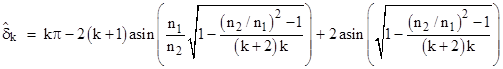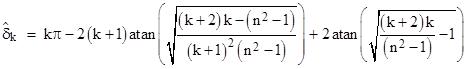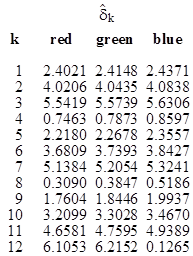The Twelfth Rainbow

This is the token of the covenant which I make between me and you… I do set my bow in the cloud…And it shall come to pass, when I bring a cloud over the earth, that the bow shall be seen in the cloud, and I will remember my covenant… and the waters shall no more become a flood to destroy all flesh.

Although rainbows have been a subject of interest and wonder since the earliest recorded history, the first qualitatively accurate explanations appeared only around the year 1300, such as an account given by Theodoric of Freiberg in 1307. Prior to this, most people had accepted the explanation of Aristotle, who taught that the rainbow was due to simple reflection of sunlight off the outer surfaces of raindrops. Theodoric was among the first to suggest that the appearance of a (primary) rainbow involves two refractions and one internal reflection. (In the Opticks, Newton claimed that “this was understood by some of the Antients”, but didn’t name them.) A more detailed account of this idea, along with the explanation of secondary rainbows, was published by the Marco Antonio de Dominis in 1611, followed by the more quantitative analysis of Descartes in 1637. (Newton remarked that the work by de Dominis, published in 1611, was “written above 20 years before”, paralleling the long delay between composition and publication of Newton’s own Opticks.) These explanations were mainly concerned with the ring of illumination, so it remained for Newton to account for the colors of the rainbow in terms of differential refrangibility.

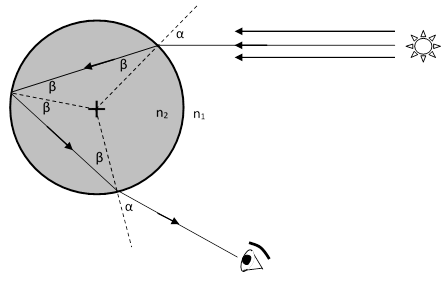
The basic explanation for a primary rainbow is illustrated in the figure below.

Snell’s law of refraction for a ray of light passing through a boundary between media with indices of refraction equal to n₁ and n₂ is

where α and β are the angles of incidence and of refraction (respectively) from the surface normal. The overall angle through which the incoming light ray from the sun is turned equals

This is for a ray that is reflected just once, but in general we can consider a ray that is reflected (inside the droplet) k times. Each reflection turns the ray through an additional angle of π – 2β, so the ray with k reflections (and two refractions) turns through a total angle of

Substituting for β from Snell’s law, the formula for the turning angle δ_k(α) for a ray with k reflections as a function of the incidence angle (i.e., the angle α that the sun’s ray makes with the surface normal) is

A plot of π - δ₁(α) and δ₂(α) – π is shown in the figure below, for angles of α ranging from 0 to π/2.

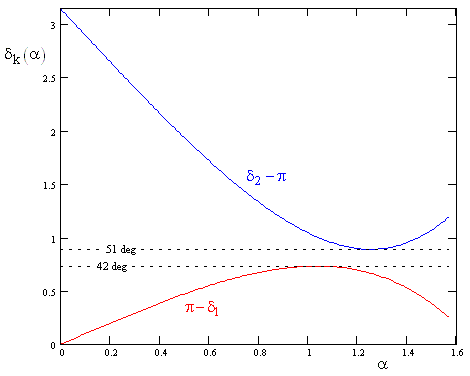
Each of the parallel incoming rays from the sun maps to a certain incidence angle α in the range from –π/2 to π/2 (with a density proportional to cos(α)), and the curves in the figure above show the angles to which those rays are directed. There will be a clustering of rays near the extremal angles, and none beyond those angles. (The cosine factor attenuates the increased clustering somewhat, but there is still a distinct local maximum of intensity at the extremal point.) As a result, the primary rainbow appears at about 42 degrees away from the axis of the sun’s rays (in the opposite direction), and the secondary rainbow appears at about 51 degrees. None of the primary or secondary rays fall in between those two angles, which explains why the region between the primary and secondary rays appears dark. A plot of intensity of the primary rays as a function of angle is shown in the figure below.

This plot actually shows the energy density contributed by the incidence angles below the peak separately from the intensity contributed by the incidence angles above the peak. The size of the droplet is considered negligible, so these two essentially contribute to the same out-going ray. The total energy in the out-going rays between two angles equals the sum of the integrals of these two curves between those angles. Note that even though the density goes to infinity at about 42 degrees, the total energy from any angle up to this limiting angle is finite. (In the above plot we have neglected the fact that each refraction and reflection is actually a combination of both, splitting the incoming rays.)

We can derive an analytical expression for the limiting angle of the kth rainbow by first differentiating equation (1) and setting the result to zero. This leads to the value of α at which the function is extremal

Substituting this back into equation (1) gives the limiting angle for the kth rainbow.

It is sometimes convenient to write this in terms of inverse tangent functions as

where we have put n = n₂/n₁. Of course, the refractivity of water, denoted by n₂, is actually a function of wavelength, ranging from about 1.331 for red light, to about 1.336 for green light, to about 1.345 for blue light. We can take the refractivity of air, denoted by n₁, to be essentially equal to 1, so for our purposes n = n₂. With these values we can determine the angles of the various colors of each rainbow, relative to the direction of the sun’s rays, as listed in the table below (with the angles reduced modulo 2π).

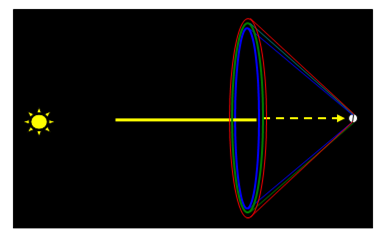
For each color and value of k, a spherical droplet projects a cone of rays, with the same axis as the sun’s rays. This is illustrated in the figure below for the primary rainbow.

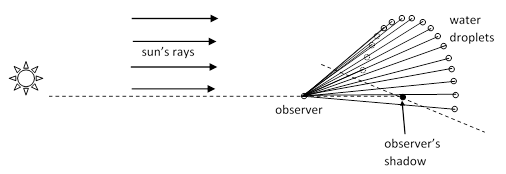
Of course, any particular vantage point resides on the cones emanating from an arc of droplets, so an observer receives a ray from each droplet, and these rays comprise a typical visual rainbow, as depicted in the figure below. Note that, for a primary rainbow, the contributing droplets are those at about 42 degrees away from the direction of the observer’s shadow.

The drawing depicts only the rays of one particular color. The colors with less refraction (for the primary bow) arrive at a greater angle from the observer’s shadow, so they originate from an arc of droplets above the arc depicted here.

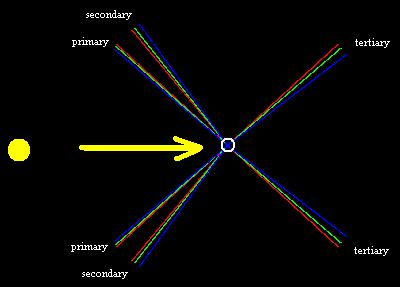
The actual angles for the primary, secondary, and tertiary rainbows are shown in the figure below.

This shows that, for a primary bow, the observed arc of colors consists of blue on the lower (inner) side, and red on the upper (outer) side of the bow. On the other hand, for a secondary bow, which appears above the primary, the order of colors is reversed, with red below and blue above. The picture also shows that, to see a tertiary bow, the observer must face the sun, and then look about 40 degrees away. The red portion of the bow will be on top, and the blue portion will be on the bottom (just as for a primary bow).

It’s remarkable that the measured angles of all these rays agree so precisely with the values computed on the basis of the assumption that the water droplets are perfectly spherical. We are accustomed to thinking of falling raindrops as having an elongated shape about the vertical axis, so we couldn’t expect such raindrops to yield the same angles for refracted / reflected rays. Presumably the water droplets suspended in clouds are small enough that their surface tension predominates over any asymmetrical aerodynamic pressures, and results in nearly perfect sphericity. (Note that the analysis is not affected by the size of the droplets.)

In 1868 Maxwell published in the Edinburgh Royal Society Proceedings a brief account of a bow he had observed on the surface of ice.

On the 26th of January, about noon, I observed the appearance of a coloured bow on the frozen surface of the ditch which surrounds S. John’s College, Cambridge. Its appearance and position seemed to correspond with those of an ordinary primary rainbow.  I at once made a rough measurement of the angle on the board of a book which I had with me, and then borrowed from Dr Parkinson, President of S. John's College, a sextant with which I found that the angle between the bright red and the shadow of the large mirror was  41° 50', and that for bright blue 40° 30'.  The angle for the extreme red of the primary bow, as given in Parkinson's Optics, is 42° 20', and that for violet  40° 32'.  The bows formed by ice crystals are seen on the same side the sun, and not on the opposite side.  I suppose the bow which I saw to be formed by small drops of water lying on the ice… How  a  drop of water can lie upon ice without wetting it, and losing its shape altogether, I do not profess to explain… I was not able to get near enough to the place where the bow appeared to see if the supposed water drops really existed.

Evidently Maxwell was somewhat surprised that the spherical water droplets presumed to be responsible for the bow would really exist in those circumstances, and yet the closeness of agreement between the observed and the calculated values seems to imply that they do. (He also noted that if the droplets were flattened on the bottom, the angles of the emerging rays would be altered as if the index of refraction had increased.)

In addition to its interest as a technical description of an optical phenomenon, Maxwell’s account is also intriguing on a human level, because of the incidental details he included. The tone is set in the very first sentence, where he reports the exact date and time of day, and refers prosaically to the ditch surrounding St. John’s College. Of course these details have (arguably) some relevance to the phenomenon, but they set it apart from most accounts of scientific experiments. Even more intriguing is his naming of the person (Dr. Parkinson) who loaned him the sextant, and identifying him as the president of St. John’s. This might come across as irrelevant information (if not name-dropping), until we learn in the next sentence that Maxwell found the theoretical angles for a primary rainbow in the book on optics written by the same Dr. Parkinson. It seems to me that this synchronicity was part of what Maxwell was trying to convey (in his characteristically under-stated way) in this little account. There often seems to be a spiritual or emotional component to the experience of observing a rainbow, as if it has some mysterious personal significance for the individual.

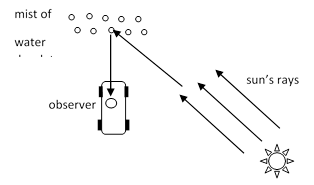
In mid October of 2002, while driving  on highway I-405 toward Valley General hospital in mid-afternoon, I observed remarkably vivid and full primary and secondary rainbows during an intense sun-shower. This highway follows an “S” shaped path going mostly eastward, and a thick mist of water droplets filled the air, some from the precipitation and some from the spray raised by other cars on the wet pavement. The lighting conditions were extraordinary, with bright sunlight piercing through a clear opening in an otherwise darkly-clouded sky. The rainbows were visible all the way to the ground, and one “foot” of the primary bow came down to a particular spot ahead of me on the curving road. I somehow expected the apparent bow to recede as I approached that spot, but it remained in place. I actually drove into, and through, this vivid wall of shimmering iridescent colors. There was no opportunity to make any measurements, but I presume the situation was as shown below.

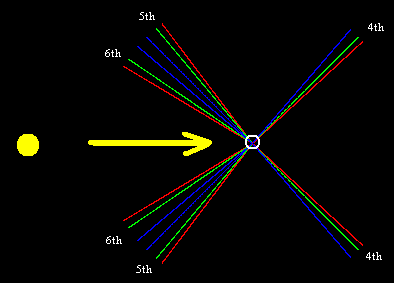
Usually the only observed rainbows are the primary, the secondary, and (much less often) the tertiary rainbows. Even more rare are reports of the 4th rainbow, which, like the 3rd, is on the sunward side of the observer. With each additional reflection inside the water droplet, the emerging ray becomes more faint (because some of the incident energy is refracted rather than reflected), so the higher-order bows are not visible to the naked eye, but in theory they are all present to some degree. The angles of the 4th, 5th, and 6th bows are shown in the figure below.

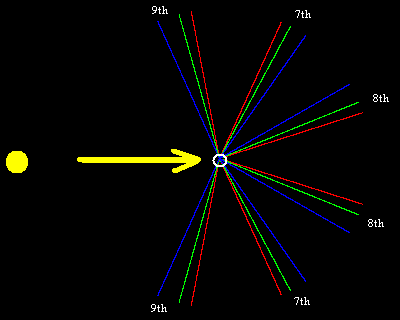
Thus the 5th and 6th bows appear in roughly the same directions as the primary and secondary bows, although the arrangements of the colors are reversed, and the colors are spread more widely. The theoretical 7th, 8th, and 9th bow angles are illustrated below.

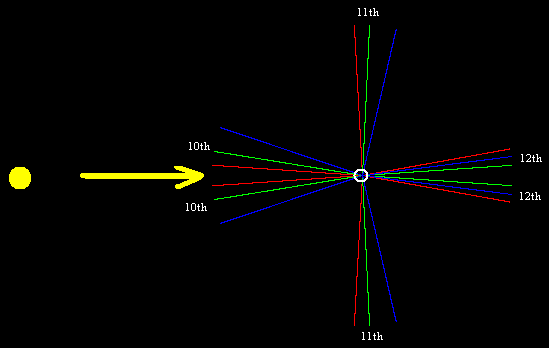
This shows that the 7th and 8th bows appear in the sunward direction, whereas the 9th bow appears at nearly 90 degrees from the direction of the observer’s shadow. Lastly, we show the theoretical 10th, 11th, and 12th bow angles.

Notice that, for the 12th bow, it appears the spectral colors are out of order, because the blue rays appear in between the red and green rays. This is because the angles of the blue rays exceed 2π, so the cone has shrunk to zero and then increased again.

Return to MathPages Main Menu