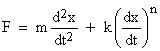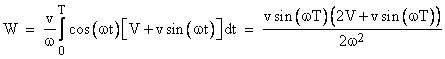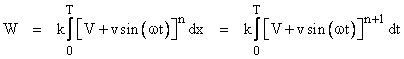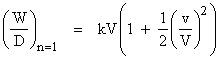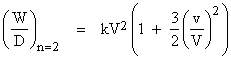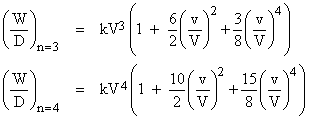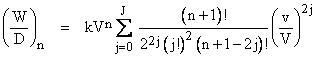The Effect of Variations in Speed

If an object moves through a resisting medium, in which the drag is proportional to the nth power of the speed, then the work done to move the object a given distance in a given time depends on whether the object’s speed is held constant or varies periodically. To illustrate, consider an object moving along the x axis with a speed that varies sinusoidally as a function of time according to the equation

where V, v, and ω are constants. The force required to move the object is given by

where m is the object’s mass, k is a constant of proportionality for the drag, and n is a constant exponent determined by the effective drag law. The work done on the object is given by the integral

We can evaluate the two components of the force separately. Intuitively we don’t expect the inertial component to give any net work, because it is out of phase with the speed, such that at each speed the object spends an equal amount of time being accelerated and decelerated at equal (and opposite) rates. Hence we expect the net work on the object to be zero, consistent with the fact that this is a conservative process. Of course, in the absence of drag, equal and opposite forces would be needed to accelerate and decelerate the object, and both would involve work. In one case work is done on the object, and in the other case the object does work. The net work applied will be zero only if we can absorb the work done by the object during deceleration, and apply it to the acceleration. However, when combined with a drag force of greater magnitude, the decelerations simply reduce the amount of positive work done on the object, so the net contribution of the inertial term is zero. In effect, we apply the work done by the object during decelerations immediately to reduce the amount of work needed to overcome the drag at the same moment, so no storage of the work energy is required in this circumstance.

To verify that the inertial term contributes a net work of zero, we can differentiate the speed to give

Thus the integral of the inertial component of the force is

Replacing dx with (V + v sin(ωt)) dt and carrying out the integration from t = 0 to T gives

This is a bounded function and periodically equals zero, whereas the distance traveled in the time T, found by integrating the speed from t = 0 to T, is

which increases without limit as T increases. Thus the long-term work per distance traveled goes to zero. This merely confirms that the inertial aspect of the motion is a conservative process.

However, for the drag component, we expect to find not only a positive amount of net work required to move a certain distance, but also a variation in the net amount of work required, depending on the oscillation in the speed. This variation is due to the fact that, unlike the inertial component, the drag component of the force is in phase with the speed. The greater the speed, the greater the drag. Now, it’s true that the object will spend the same amount of time with an increase in drag as with an equal and opposite decrease in the drag, but work is proportional to the distance traveled, not to the time. The periods of increased drag correspond to increased speed, so a greater distance is traversed than during the same amount of time spent at reduced speed. Hence, even if drag is directly proportional to speed, we expect that any oscillations in speed will result in a net increase in the total work required to move the object a given distance in a given time. The minimum amount of work corresponds to maintaining a constant speed.

To evaluate this effect quantitatively, we just need to evaluate the integral of the drag force, which gives

With n = 0, meaning that the drag force is constant, independent of the speed, this evaluates to W = kD plus some bounded periodic terms, so the work per distance traveled is simply k, as we would expect. However, if the drag is directly proportional to the speed, we have n = 1, and the integral give

Only the terms proportional to T have significance for the net long-term work over many cycles, because the other terms are bounded and periodic, so the secular work for large T is simply

Likewise the secular distance traveled in the time T is just VT, so the work per distance traveled is

This confirms that, if drag is directly proportional to speed, the minimum work per distance, kV, occurs with the oscillation amplitude v equal to zero.

By the same analysis we can determine the work per distance for higher exponents. For example, if drag is proportional to the square of the speed (i.e., n = 2), we find that the work for moving a given distance in a given time

Thus the fractional increase in work per distance for a given amplitude of speed oscillation is three times as great if drag is proportional to the square rather than to the first power of the speed.

Carrying on the analysis to higher exponents in the drag law, we find the results

and so on.  In general have

where J is the integer part of (n+1)/2. Since this is always an “even” function, the work per distance is always greater than or equal to kVⁿ, and equality applies only in the limiting special case of zero deviations from uniform speed. Any perturbation at all will result in an increase in the required work to travel a given distance in a given time. (Of course, this neglects variations on the order of a single cycle.)

There seems to be an interesting correspondence between this result and the second law of thermodynamics. An object can be pushed a given distance in a given time in infinitely many ways, even if we consider only straight-line monotonic paths. Moving the object a given distance at constant speed through a resisting medium is similar to transferring heat from one temperature to another in the most efficient possible way. Any variability in the process results in reduced efficiency and an increase in entropy.

Return to MathPages Main Menu