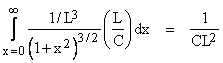Null Cones in Cylindrical Dimensions

In the 1920’s Kaluza attempted to incorporate electromagnetism into the geometrical framework of general relativity by postulating a fourth spatial dimension, and he suggested that this dimension has gone unnoticed because it is cylindrical with a very small circumference. Eventually the theory of Kaluza and Klein came to be seen as merely a formal rather than a substantial unification, but the idea of one or more small “curled-up” dimensions has subsequently re-appeared many times in the speculations of physicists, notably in modern “string theory”.

From a naïve point of view, assuming all the spatial dimensions are locally equivalent, differing only in their topology, a cylindrical dimension raises several interesting physical issues. For example, it’s known that Huygens’ principle “works” only in spacetimes with an odd number of spatial dimensions, so Huygens’ principle would not apply in a spacetime with any odd number of “curled-up” dimensions – at least not on the scale of the cylindrical circumference.

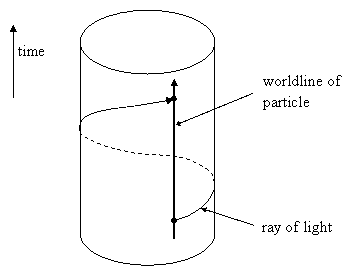
It’s also interesting to consider the null-cone structure of a spacetime with a curled-up dimension. Rays of light (or photons) emitted from a point-like particle in the direction of the cylindrical dimension would presumably travel around the circumference and be re-absorbed by the emitting particle at a later time, as shown below.

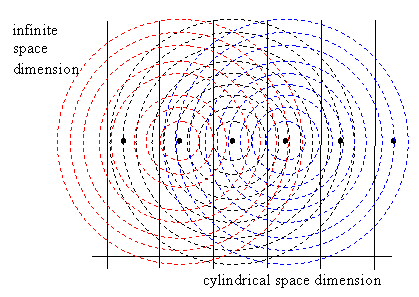
Each timelike worldline actually intersects infinitely many times with the null cone emanating from any given point on the worldline. The time interval between each emission and self-absorption would be C/c, where C is the circumference and c is the speed of light. Of course, a spherical shell of light would expand in all directions, not just the cylindrical direction, so the intensity of the absorptions would drop off for successive intersections (even assuming the wavefront could pass through previous intersections undisturbed). One way of looking at this is to show two space dimensions, one infinite and one cylindrical, and represent the latter as an infinite dimension with periodicity. In other words, we consider a normal doubly-infinite two-dimensional space, but consisting of repeated slices in the cylindrical direction, as illustrated below.

Each of the regions separated by vertical lines is a repetition of the same finite cylindrical “surface” (unrolled), and all the particles shown in this figure are actually the same particle. An expanding spherical electromagnetic wave propagates outward from a particle, and impinges on that same particle repeatedly thereafter, from both directions. By the same token, another particle would be struck by the expanding wave infinitely many times. This is another illustration of why Huygens’ Principle doesn’t work under these conditions, because a single pulse of light will not pass distant particles as a sharp single pulse, but rather as an infinite series of pulses of diminishing strength, as the wave repeatedly circumnavigates the cylindrical dimension.

Assuming three infinite spatial dimensions and one cylindrical dimension, the energy of a spherical pulse is spread over a “spherical” surface in four-dimensional space, and the volume of this three-dimensional manifold is proportional to the cube of the radius. Therefore, assuming conservation of energy, the energy intensity must drop off in proportion to the reciprocal of the cube of the distance. The distances between two particles (aligned with the cylindrical axis) are of the form

where L² = Dx² + Dy² + Dz² and C is the cylindrical circumference. Thus the cumulative energy of all the impingements (per unit cross-section) is proportional to the infinite sum

Since C/L is assumed to be very small (i.e., the extra cylindrical dimension is very small compared with the typical macroscopic distance L with which we are concerned), these summations over j are closely approximated by integrals over the variable x = jC/L. Noting that dj = (L/C)dx, it follows that a spherical pulse of light imparts to a unit cross-section at distance L a total cumulative energy proportional to

In this way we recover (at large scales) the inverse-square relation, which was to be expected, since the extra cylindrical dimension can’t accumulate energy. However, as noted above, the energy from the instantaneous emission at the source arrives not as a single instantaneous pulse but “smeared out” over infinitely many smaller pulses. The first of these pulses arrives at time L/c, but subsequently more pulses arrive, with intensities that decay with time. The distance increases roughly linearly with time, so the intensity drops off approximately as the inverse cube of the time. No such “smearing out” in time is observed (in accord with Huygens’ Principle), so this suggests that either there is no extra cylindrical dimension, or, if there is, that light does not propagate through it in the same way it propagates through the other three spatial dimensions.

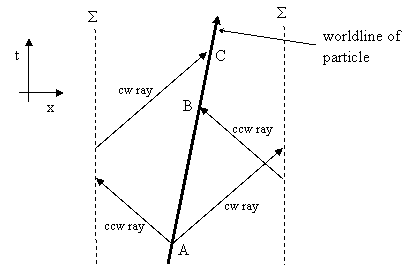
The idea of a small cylindrical dimension also has implications for the ontological status of space and time. Consider just a single cylindrical spatial dimension x and a time dimension t, drawn by unrolling the space dimension and identifying two parallel slices Σ as shown below.

At event A the particle emits light rays in the clock-wise (cw) and counter-clockwise (ccw) directions. Each ray propagates around the cylindrical dimension and returns to the particle from the opposite direction. However, since the particle is moving, the ccw ray strikes it at event B, whereas the cw ray strikes it at event C. Thus the absolute motion of the particle can be inferred from the time lag between B and C. If the particle was at absolute rest (meaning its worldline would be a vertical line in the figure above), the cw and ccw rays would return to the particle simultaneously. This is essentially just an instance of the Sagnac effect, except that it applies to translational (linear) motion in a closed cylindrical dimension. Needless to say, this effect is not unique to light rays. The same effect would appear for identical bullets shot from identical guns in the two directions.

The implication would seem to be that translational motion in a cylindrical dimension of space it absolute, just as rotation is absolute in ordinary spaces. In this context the overall momentum of all the matter in the universe could have some non-zero value. Kurt Gödel is often credited with being the first to find solutions of the field equations of general relativity such that the overall mass of the universe is rotating, a discovery that is seen as having profound implications. However, the same implications can be drawn from this trivial example of a cylindrical universe. This raises Machian questions as to the source of the absolute frame. In our hypothetical cylindrical universe there exists only a single particle, and yet it appears that the particle has a physically meaningful state of absolute motion, i.e., it can be “in motion” relative to the space in which it resides. The spacetime itself imposes a well-defined state of absolute rest, albeit only globally. If we restricted our attention to phenomena in a small region of the cylindrical space we would find that it is still Minkowskian, meaning that special relativity still applies, and there is no locally distinguished state of absolute rest. It is only when we identify the two slices labeled Σ as being the same slice that we introduce a global absolute rest. This seems to support the substantivalist view of spacetime (even locally flat spacetime) as an entity with its own independent existence and properties, prior to the introduction of any material particle.

Of course, in general relativity the metric field of spacetime is itself a physical entity (one that both acts and is acted upon), so in a sense the dichotomy between substantivalism and relationism is moot. Nevertheless, the physical prominence of the spacetime’s state of motion in the hypothetical flat cylindrical space illustrates how strongly the global topology can affect the observable physics. The null cone and, more generally, the inertial structure of spacetime, combined with the cylindrical topology, seem to confer ontological status to spacetime.

To some extent this is conventional, because we are not required to identify the two S slices, and we are not required to associate the signals received at events B and C with the signals emitted at A. We could insist that the space dimension is infinite, and just happens to contain multiple correlated copies of the same physical entities. For example, for each clock in our local region, there are infinitely many other seemingly identical clocks located at equally-spaced distances in both directions, as shown below.

The readings on these clocks define one particular locus of simultaneity, but we are not logically required to regard this as the true or absolute simultaneity. It just so happens that whenever we try to change the synchronization of the clocks by changing our local clock, an infinite number of identical beings change all the other clocks by the same amount, so we are left with the original synchronization. Needless to say, the most natural interpretation of these observations would be that the universe is cylindrical, even though this interpretation is not logically necessary. By identifying all those clocks as “the same clock”, we accept that the locus of simultaneity indicated by those clocks (or rather, by that clock) is the true and absolute simultaneity.

In a cylindrical universe (or even in a normal universe with three space dimensions plus one small cylindrical dimension) the null cone emanating from any given event intersects with itself infinitely many times. As a result, the absolute character (spacelike, null, or timelike) of intervals is lost. In such a space, there exist multiple geodesic paths between two given events, and some of these geodesics are spacelike, some are timelike, and some are null. The causal structure of such a spacetime (if it existed) would be very complicated.

Return to MathPages Main Menu