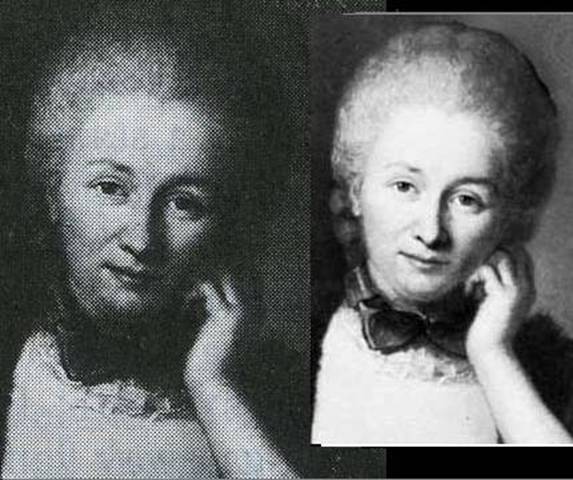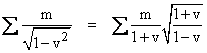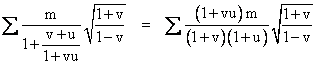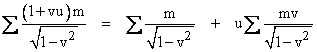The Portraits of Emilie du Chatelet

The first translation of Isaac Newton’s Mathematical Principles of Natural Philosophy from the original Latin into French was made by Emilie du Chatelet (1706-1749). This would be an impressive accomplishment for anyone, but it’s even more remarkable for a woman, considering the limited opportunities that were available to women in those days, and considering that Mme du Chatelet also raised three children and found time to carry on love affairs with several prominent (and some not-so-prominent) men. In addition to her husband (the marquis Florent du Chatelet, whom she married at 19), she had affairs with the Duc de Richelieu, Voltaire, Maupertius, Comte de Guébriant, Clairaut, and Jean Francious Saint-Lambert.

Several portraits of her exist, but the most popular is the one that depicts a woman seated at a desk, holding a compass in one hand over some kind of mathematical text (presumably the Principia) as shown below.

Oddly enough, there seem to be a number of subtly different versions of this portrait in circulation. For example, a portion of the version contained in the 1969 Encyclopedia Britannica is shown below on the left, and on the right is an enlargement of the face from the above version.

Clearly the facial features, while similar, are not identical. The image from Britannica (on the left) seems more womanly and maternal, whereas the image on the right seems slightly girlish. Also, the gaze of the Britannica Emilie is averted slightly to her left, whereas the image on the right makes direct eye contact with the viewer. The difference is most noticeable in the left eye and in the curve of the nose. Is the effect just due to differences in brightness and contrast in the reproductions, creating an optical illusion of slightly different features, or are these two paintings actually different?

The sources of these images is hard to determine. The Britannica article includes the following note beneath the image:

MME DU CHATELET. PORTRAIT BY AN UNKNOWN ARTIST. IN A PRIVATE COLLECTION.

This seems oddly mysterious for an encyclopedia. Evidently the painting is unsigned, and there is no record of who painted it. Also, the owner of the painting (in 1969) preferred not to be identified. It would be interesting to know more about the background of this painting, and where the original resides (assuming there is just a single original). There can hardly be any doubt that it’s a painting of Emilie Chatelet, because no other woman of that time would have been portrayed working with a compass over a mathematical text. Still, the variation in features is odd. Still another version of what appears to be essentially the same portrait is shown below.

Again the facial features are noticeably different. It’s as if many copies of some original painting were made, and each copyist saw her – or chose to portray her – in his own unique way.

The other existing portraits (three of which are shown below) don’t provide many hints as to which version is more accurate, because she looks quite different in each of them, and none of them much resembles the woman with the compass.

Eye-witness accounts are not much help either, because some of the people who knew her described Emilie as quite beautiful, whereas her cousin described her as distinctly ugly and ungainly. We do know Emilie dressed as a man once to gain entrance to a scientific conference, after she had been asked to leave when dressed as a woman. After her death, Voltaire wrote to Frederick that she was “a great man, whose only fault was to be born a woman”. Perhaps the artist who painted the portrait below was trying to pay her a similar compliment.

Emilie did not became interested in science and mathematics until the age of 27, at which point she hired private tutors (including Maupertius) to help with her studies. Originally she was greatly influenced by the writings of Leibniz, and wrote an overview of his work (Institutions of Physics), but she later shifted her attention to Newton’s work and adopted the Newtonian view of physics almost completely – as did her lover and lifelong friend Voltaire. The one notable exception was in the debate over Leibniz’s vis viva (living force), which is proportional to what we would call kinetic energy, and which Emilie believed was more fundamental and important than momentum. In contrast, momentum was regarded by the followers of Descartes as the true measure of motion, and it also plays the central role in Newton’s physics. This was at a time when people were first beginning to think about physics in terms of conserved quantities, and these quantities were seen as having philosophical implications because people tended to regard conserved quantities as representing “true” ontological entities. Thus the true constituents of the world could be identified by determining the fundamentally conserved quantities.

The classical science of mechanics implicitly assumes that the sum of the masses in a given closed system is constant. (This was subsequently extended by Lavoisier to chemical processes as well.) In addition, Newton’s laws imply that the sum of the momentums is constant, where momentum is defined as the product of mass and velocity. Of course, velocity is a vector, so momentum is also a vector, but in one dimension we can regard it as a scalar. Newton’s Principia makes extensive use of the concept of momentum, which Newton called the “quantity of motion”. On the other hand, Leibniz emphasized the significance of what he called vis viva, defined as the product of mass and the square of the velocity. Even though “vis” means literally “force”, this quantity is proportional to what we call the (classical) kinetic energy of a massive particle. Thus we have the three putative conserved quantities

All higher-order quantities, such as the sums of the quantities mv³, mv⁴, and so on, are redundant to the three listed above (together with the assumption of simple additivity), because the conserved quantities for all combinations of any number of entities follow from how the quantities behave for just two discrete particles. To see this, notice that once we’ve determined that any given subset of a large number of particles has constant values for certain conserved quantities, we can consolidate them into a single abstract entity, and then evaluate the interaction of this aggregate entity with one other entity. Thus it is sufficient to consider how just two entities interact. Now, if two entities with speeds v₁ and v₂ jointly have conserved momentum and conserved kinetic energy, then v₁ + v₂ = k₁ and v₁² + v₂² = k₂ for some constants k₁ and k₂. All quantities of the form v₁ⁿ + v₂ⁿ can be expressed in terms of k₁ and k₂, so it follows that all these quantities are constant. In other words, the conservations of momentum and kinetic energy, combined, are necessary and sufficient (at least in one dimension) to imply the conservation of all higher-order quantities.

Today we regard energy and momentum as complementary (indeed they are just different components of the energy-momentum tensor), but the natural philosophers of the early 18th century thought one or the other must be more fundamental, i.e., more “real”. The fervor of the debate may have been fueled in part by the nationalistic rivalries between the supporters of Descartes, Newton, and Leibniz. In any case, Emilie correctly recognized that the vis viva of Leibniz (following Huygens) had profound physical significance. Reviewing the controversy from the standpoint of the late 19th century, Mach commented

We now know that both the Cartesian and the Leibnizian measure of the effectiveness of a body in motion have, each in a different sense, their justification… The investigations of Newton really proved that for free material systems not acted on by external forces the Cartesian sum ∑mv is a constant, and the investigations of Huygens showed that also the sum ∑mv² is a constant, provided work performed by forces does not alter it. The dispute raised by Leibniz rested, therefore, on various misunderstandings. It lasted 57 years, till the appearance of D’Alembert’s Trait de dynamique, in 1743.

Interestingly, despite his dismissal of the significance of the dispute over vis viva, Mach was very impressed with an elementary argument of Schutz (1897) showing how the conservation of kinetic energy (or vis viva), together with a relativistic assumption, actually implies the conservation of momentum. Schutz pointed out that if the sum ∑mv² for a system of particles is a constant, then for any fixed velocity u the sum

ought to also be a constant. The first sum on the right side is just the original constant kinetic energy, and the last term is also a constant, so the middle term on the right side must be constant for any u, which implies ∑mv is constant. A similar argument applies in the context of special relativity. For simplicity, consider a system of co-linear particles, and note that the conservation of mass-energy is expressed by the constancy of the sum

To offset this arrangement of particles by an arbitrary speed u, each term in the summation must be multiplied by the constant square root of (1+u)/(1–u), and each v in the denominator of the leading factor of the summation must be replaced with (v+u)/(1+vu). Canceling out the constant square root factor, this leads to the constant summation

Dividing through by (1+u) and simplifying, this implies the constancy of

for any speed u. The first sum on the right side is just the original constant mass-energy, and the second summation on the right side is the relativistic momentum, so (again) the momentum is constant. From this perhaps Leibniz and du Chatelet might claim some vindication for their belief in the primacy of vis viva. (From a sociological standpoint it might be argued that vis viva, mv², is a feminine quantity, whereas vis mortua, mv, is masculine. This would be in keeping with the “xx” squared female chromosomes and the “xy” linear male chromosomes. One might also try to interpret the difference between scalar and vector quantities in terms of gender.)

Emilie’s most enduring and meaningful relationship was with Voltaire, extending from 1733 to her death in 1749. The two of them were largely responsible for popularizing Newton’s scientific principles on the continent. Ten years after her death, Voltaire saw to the publication of Emilie’s translation of the Principia, which remains to this day the standard French version. The frontispiece of the first edition contained the image shown below, in which Emilie du Chatelet is shown as an angelic intermediary, reflecting Newton’s light down to Voltaire.

At the age of 42, nearing the completion of this translation, Emilie became pregnant by the poet Saint-Lambert. At this time she was living (along with Voltaire) in the Court of Stanislas, former King of Poland, then living in exile in Lorraine. Emilie had been invited there as part of a ploy to lure Stanislas away from his mistress. Nothing came of the scheme, except that Emilie and Stanislas’ mistress became close friends, and Emilie started an affair with Saint-Lambert. She gave birth to a baby girl, but died six days later, with her husband Chatelet, her lover Saint-Lambert, and her former lover Voltaire all attending her, and the baby died a few days later.

Return to MathPages Main Menu