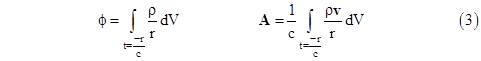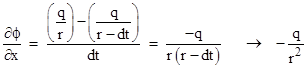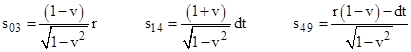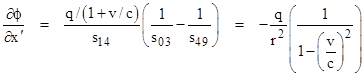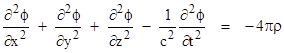Retarded and Advanced Potential

In classical electrodynamics the electromagnetic force F on a charged test particle at any given time and place can be expressed in terms of the electric and magnetic fields E and B and the velocity u of the test particle by Lorentz’s equation

where q is the charge of the test particle (assumed to be small enough so as not to act as a significant source itself). One convenient way of evaluating the fields E and B in terms of the positions and velocities of the surrounding charges is by means of a scalar field ϕ and a vector field A, called the electric and magnetic potentials, defined such that

The potential fields are convenient because their values at any given event can be expressed as simple integrals of the charge density ρ and velocity v over the volume of the past light cone of the event, as follows

where r is the spatial distance from the event in question (with respect to any specified inertial coordinate system). Since the integrals are evaluated over the past light cone of the event, the functional expressions for the charge density and velocity appearing in these integrands are r(r, –r/c) and v(r, –r/c), with the understanding that we have set t = r = 0 at the event in question. Notice that if v is constant, then A = (v/c)ϕ, and equations (2) can be written as

Also, note that the total differential dϕ for any given differentials dt, dx, dy, dz is

For an incremental path co-moving with the charged source particle with velocity v, we have dϕ/dt = 0 for fully developed fields (i.e., the field is in a fixed co-moving configuration with the source), so if we divide through the above equation by dt and re-arrange terms we get

Making this substitution in (4), we can express the electric field due to charged particle moving with constant velocity v as

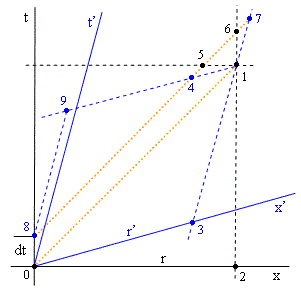
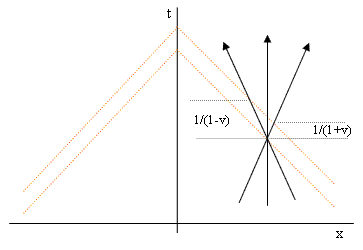
It’s worth noting that the integral expression (3) for the electric potential indicates that the contribution of each stationary point-like element of charge q is q/r where r is the spatial distance, but this distance depends on the choice of inertial coordinate system. The spatial and temporal lengths of a null interval can both be made arbitrarily small by choosing a suitable inertial frame, and yet the charge q is invariant, so it might seem as if the electric potential is singular, because we can make q/r as large as we like, simply by choosing an inertial coordinate system with respect to which r is arbitrarily small. However, the Lorentz covariance of space, time, and electromagnetism fields ensures that a self-consistent picture of the observable phenomena is given, regardless of which inertial reference frame we choose. To see in detail how this happens, consider the interaction shown below.

We first evaluate this with respect to the unprimed x,t coordinate system. Let the spatial distance s₀₁ be denoted by r, so the spatial distance s₀₅ is r – dx (noting that s₁₅ = dx = dt). Hence the potential from a charge q at point 0 is q/r, and assuming the source particle moves along the t axis, it’s contribution at point 5 is q/(r-dx). From this we get the partial derivative

This is the only non-zero component of the gradient, and since v = 0, equation (5) gives the electric field as

Now consider the same situation with respect to inertial coordinates x’,t’ whose spatial origin is moving in the positive x direction at the speed v. It is straightforward to determine the magnitudes of the following intervals:

It might seem that the partial derivative of ϕ with respect to x′ would be given simply by (q/s₄₉ - q/s₀₃)/s₁₄, but this omits one important factor. Consider three charged point-like particles passing through the past light cone of a certain event as illustrated below.

The light cone is shown with a non-zero thickness to illustrate that the duration of time spent by each particle as it passes through the light cone depends on the speed of the particle. The basic charge q is defined based on the static Coulomb potential, represented by the vertical (v = 0) path. In general, the duration of coordinate time spent by a point-like particle in the light cone shell is proportional to 1/(1 + v/c). This proportionality remains the same, regardless of the thickness of the light cone shell, even in the limit as the thickness goes to zero. It is analogous to the Doppler effect, causing the “intensity” of the electric potential to be increased for approaching charges and decreased for receding charges.

In the present example the source charge is moving in the negative x direction, i.e., away from the other particle, with speed v relative to the primed coordinate system, so the effect of the charge q on the potential at the other particle is decreased by the factor of 1/(1 + v/c). Taking this factor into account, we have

This is the gradient of ϕ (because the y′ and z′ components are zero), so we can substitute into equation (5) with v = (v,0,0) to give the electric field with respect to the primed coordinates

As expected, the magnitude of the electric field (in the x direction) is the same as the value it has with respect to the rest frame coordinates. This is consistent with the conventional transformation equations described in Force Laws and Maxwell’s Equations.

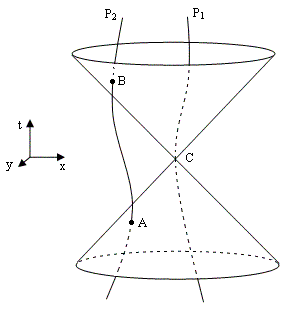
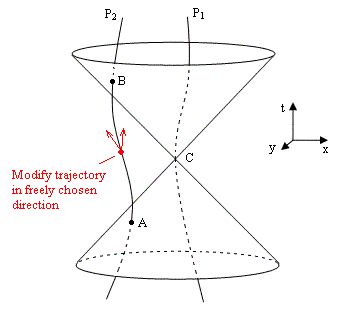
In the preceding discussion the charges were in uniform motion, but we can apply the same approach to charges in arbitrary motion. Consider two point-like particles P₁ and P₂, both with rest mass m and electric charge +q. The worldlines of these two particles may be as shown in the figure below. (Note that the particles can, in principle, be moved around by means of electrically neutral pliers, so their worldliness are essentially arbitrary timelike paths.)

The electric and magnetic potentials to which particle P₁ is subjected at the origin C (excluding those due to its own charge) are fully determined by the position and velocity of the particle P₂ at event A on the past light-cone of C. Of course, due to the temporal symmetry of Maxwell’s equations, we could just as well reverse the sign of t, meaning that the potentials at C would be determined by the position and velocity of P₂ at event B on the future light-cone of C (assuming there are no other charged particles of any significance). In other words, we can just as well use the advanced potentials, given by inserting the functional expressions ρ(r, +r/c) and v(r, +r/c) into (3). It might seem as if this would imply that the potential fields given by these two conditions must be equal, i.e., that q/r_A = q/r_B and hence r_A = r_B. However, this is not the case, because the absolute value of the potential is unobservable; only the partial derivatives of the potential are significant. Furthermore, the electromagnetic potentials are inherently under-specified in the sense that they possess a gauge symmetry, as can be seen from the fact that the electric and magnetic fields given by (2) are unchanged if we replace ϕ and A with

where Ω is a completely arbitrary scalar field. We are free to choose this function such that

but even this does not uniquely fix the potentials, because the electric and magnetic fields are also unchanged if we augment Ω by any arbitrary scalar field whose d’Alembertian vanishes. Thus there are many different potential fields that yield any given electric and magnetic fields, so there is nothing surprising about the proposition that the electric and magnetic fields at any given instant are consistent with both the advanced and the retarded potentials fields. This is somewhat analogous to the Laplacian determinism of classical mechanics, according to which the state of the universe at any given time can equally well be inferred from a complete specification of the conditions in the future as from a specification of conditions in the past. There is, however, an extra complication in electrodynamics due to the light cone structure. In order to determine the future and past states based on the state at a given instant, it is necessary to specify not only the positions and velocities of all the particles, but also the values of the electric and magnetic fields at every point. If we wished to specify only the positions and velocities of the particles, it would be necessary to specify them not just at a given instant but for all time into the past (or into the future), assuming an infinitely large universe.

In 1909 Walter Ritz and Albert Einstein (former classmates at the University of Zurich) debated the question of whether there is a fundamental temporal asymmetry in electrodynamics, and if so, whether Maxwell’s equations (as they stand) can justify this asymmetry. As mentioned above, the potential field equation

is equally well solved by either of the two functions

where ϕ₁ is called the retarded potential and ϕ₂ the advanced potential. Ritz believed the exclusion of the advanced potentials represents a physically significant restriction on the set of possible phenomena, and yet it could not be justified in the context of Maxwell’s equations. From this he concluded that Maxwell’s equations were fundamentally flawed, and could not serve as the basis for a valid theory of electrodynamics. Ironically, Einstein too did not believe in Maxwell’s equations, at least not when it came to the micro-structure of electromagnetic radiation, as he had written in his 1905 paper on what later came to be called photons. However, Ritz’s concern was not related to quantum effects (which he rejected along with special relativity), it was purely classical, and in the classical context Einstein was not troubled by the exclusion of the advanced potentials. He countered Ritz’s argument by pointing out (in his 1909 paper “On the Present State of the Radiation Problem”) that the range of solutions to the field equations is not reduced by restricting ourselves to the retarded potentials, because all the same overall force-interactions can be represented equally well in terms of advanced or retarded potentials (or some combinations of both). He wrote

If ϕ₁ and ϕ₂ are [retarded and advanced] solutions of the [potential field] equation, then ϕ₃ = a₁ϕ₁ + a₂ϕ₂ is also a solution if a₁ + a₂ = 1. But it is not true that the solution ϕ₃ is a more general solution than ϕ₁ and that one specializes the theory by putting a₁ = 1, a₂ = 0. Putting ϕ = ϕ₁ amounts to calculating the electromagnetic effect at the point x,y,z from those motions and configurations of the electric quantities that took place prior to the instant t. Putting ϕ = ϕ₂ we are determining the above electromagnetic effects from the motions that take place after the instant t. In the first case the electric field is calculated from the totality of the processes producing it, and in the second case from the totality of the processes absorbing it. If the whole process occurs in a (finite) space bounded on all sides, then it can be represented in the form ϕ = ϕ₁ as well as in the form ϕ = ϕ₂. If we consider a field that is emitted from the finite into the infinite, we can naturally use only the form ϕ = ϕ₁, precisely because the totality of the absorbing processes is not taken into consideration. But here we are dealing with a misleading paradox of the infinite. Both kinds of representations can always be used, regardless of how distant the absorbing bodies are imagined to be. Thus one cannot conclude that the solution ϕ = ϕ₁ is more special than the solution ϕ = a₁ϕ₁ + a₂ϕ₂ where a₁ + a₂ = 1.

Ritz objected to this, pointing out that there is a real observable asymmetry in the propagation of electromagnetic waves, because such waves invariably originate in small regions and expand into larger regions as time increases, whereas we never observe the opposite happening. Einstein replied that a spherical wave-shell converging on a point is possible in principle, it is just extremely improbable that a widely separate set of boundary conditions would be sufficiently coordinated to produce a coherent in-going wave. Essentially the problem is pushed back to one of asymmetric boundary conditions.

Ritz died in July of 1909 at the age of 31, just six weeks after the last published exchange with Einstein appeared. Later that same year, Einstein published another paper, in which he again addressed the subject of reversibility for electromagnetic interactions, acknowledging that “our theory of light cannot explain certain fundamental properties of light phenomena”, providing a list of phenomena for which existing theory seemed inadequate. He continued

The basic property of the [classical] wave theory that gives rise to these difficulties seems to me to lie in the following. While in the kinetic theory of matter there exists an inverse process for every process in which only a few elementary particles take part (e.g., for every molecular collision), according to the wave theory this is not the case for elementary radiation processes. According to the prevailing theory, an oscillating ion produces an outwardly propagated spherical wave. The opposite process does not exist as an elementary process. It is true that the inwardly propagated spherical wave is mathematically possible, but its approximate realization requires an enormous number of emitting elementary structures. Thus, the elementary process of light radiation as such does not possess the character of reversibility. Here, I believe, our wave theory is off the mark. Concerning this point the Newtonian emission theory of light seems to contain more truth than does the wave theory, since according to the former the energy imparted at emission to a particle of light is not scattered throughout infinite space but remains available for an elementary process of absorption.

It might seem as if Einstein is conceding Ritz’s point here, by questioning the validity of the general wave solutions of Maxwell’s equations, but notice that Einstein’s reasoning is actually the opposite of Ritz, because Einstein is guided by the intuition that the elementary processes must be reversible, whereas Ritz argued for the inherent irreversibility of the fundamental processes. Both of them were led to consider “action at a distance” formulations, but Ritz was working in the classical context, whereas Einstein believed that the deficiency in Maxwell’s equations arises only in the regime where quantum effects are important. As noted above, Ritz never accepted the need for quantum theory.

Interestingly, 30 years later, Richard Feynman as a young graduate student gave his first formal talk at a seminar at Princeton on the subject of advanced and retarded potentials in electromagnetism. Feynman and his advisor John Wheeler had developed a theory of direct interaction (dispensing with classical fields) by using half advanced and half retarded potentials, similar to the theory developed by Dirac in 1938. Feynman’s autobiographical book “Surely You’re Joking Mr. Feynman” includes a chapter entitled “Monster Minds”, in which he recalls his alarm upon learning, shortly before the talk, that the attendees would include Henry Norris Russell, John von Neumann, Wolfgang Pauli and Albert Einstein. Just as the talk was about to get started, Feynman was writing some equations on the blackboard, and Einstein walked in and said “Hello, I’m coming to your seminar, but first, where is the tea?” At this time, Feynman wasn’t aware of Einstein’s debate with Ritz back in 1909 on the subject to advanced and retarded potentials. It’s interesting that some of the ideas of Feynman’s talk that day, such as the need for a complete absorber in the future, were already familiar to Einstein. After the talk was over, Pauli raised some objection to the theory, and asked if Einstein agreed. “No”, Einstein replied, “I find only that it would be very difficult to make a corresponding theory for gravitational interaction”.

As we’ve seen, Einstein had answered Ritz by asserting that the electromagnetic field at a given point can calculated equally well from either the totality of the processes producing it or the totality of the processes absorbing it. This would certainly follow if all processes were symmetrical under time reversal, as are Maxwell’s equations of the electromagnetic field. However, as Einstein himself later remarked, “Maxwell’s theory of the electric field remained a torso, because it was unable to set up laws for the behavior of electric density, without which there can, of course, be no such thing as an electromagnetic field”. A first step toward completing Maxwell’s theory was provided by the Lorentz force law (1), describing how electric charges move in an electromagnetic field, but this equation is satisfactory only for sufficiently small accelerations, because it neglects the effects of a particle’s own field on itself. Attempts to create a fully satisfactory theory of classical electrodynamics, valid for arbitrary motions, seem to inevitably lead to conflicts with the principle of causality. For example, the Lorentz-Dirac equation, developed by Dirac in 1938, leads to the conclusion that if an electric is subjected to a force, it must begin to accelerate just prior to the application of the force. This conflict with the usual ideas of causality was already implicit in Einstein’s answer to Ritz, as can be seen in the figure below.

Recall that the field to which the particle at C is subjected can be calculated (according the equations for the retarded potentials) from the positions of the charges, such as A, on the past light cone of C. But the field at C can also be computed from the positions of the charges, such as B, on the future light cone of C. In Einstein’s terminology, the field at C is produced by A and absorbed by B. But suppose that, after the particle moving along the worldline P₂ has passed through event A, but before it passes through event B, we subject it to a force that changes its trajectory, so it doesn’t pass through B. Thus it seems we can set up a conflict of causality. Of course, it’s unrealistic to consider a universe with just two electrically charged particles. In more realistic models the field at C would be absorbed by more than just the charge at B. Nevertheless, if we postulate that the charge configuration in the future can be freely established by the exercise of free will, independent of the charge distribution of the past, we encounter the same conflict with causality, so it isn’t surprising that a classical theory of electrodynamics of arbitrarily moving charges leads to acausal results.

Return to MathPages Main Menu