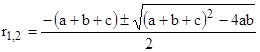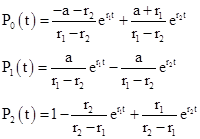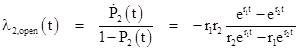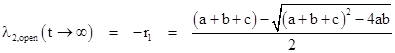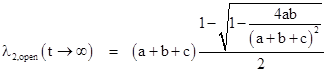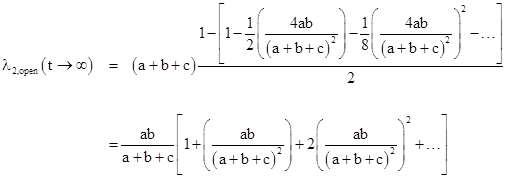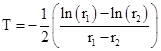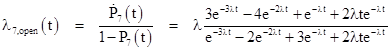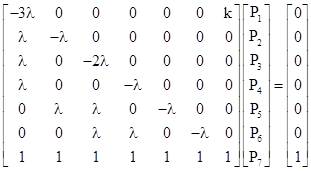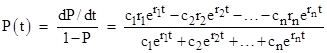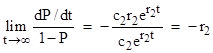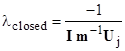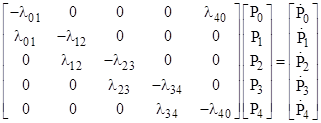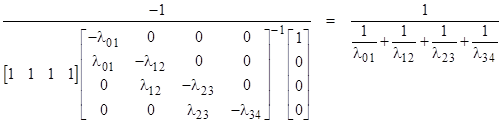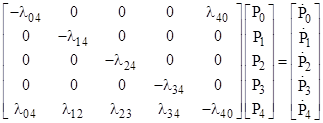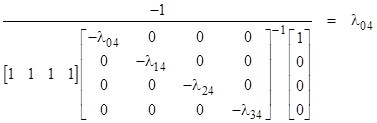Asymptotic Rate of an Open Loop Markov Model

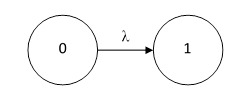
Consider the simplest possible Markov model, consisting of a single transition from State 0 to State 1 with the exponential rate λ as shown below.

The hazard rate (dP/dt)/(1-P) for State 1 is obviously just λ, but we can think of this in two different ways, which we will call “closed-loop” and “open-loop”. The closed-loop approach is to stipulate that whenever the system enters the final state it is repaired and returned to State 0. In other words, there is an implicit return path from State 1 to State 0 with some arbitrary exponential rate σ. Thus the steady-state condition is P₀ = σ/(λ+σ) and P₁ = λ/(λ+σ), and the steady-state flow rate into State 1 is λP₀ = λσ/(λ+σ). Therefore, the hazard rate for State 1 is (dP₁/dt)/(1 - P₁) = λ, just as expected. In contrast, the open-loop approach does not assume any feedback, so if all the probability begins in State 0 it flows continuously into State 1. The probabilities of the states as functions of time are P₀(t) = e^−λt and P₁(t) = 1 – e^−λt, and the flow rate into State 1 is λP₀ = λe^−λt. Therefore the hazard rate for State 1 is (λe^−λt)/(e^−λt) = λ, again just as expected. Thus the open and closed loop interpretations are equivalent for this elementary model.

However, for more complicated models the open-loop hazard rate for the nth state is a function of time, so in general it isn’t clear, a priori, how to infer the steady-state closed-loop hazard rate (for the nth state) from the open-loop behavior. One idea that is sometimes suggested is to evaluate the open-loop hazard rate in the limit as time increases to infinity. Obviously both the numerator and the denominator of the hazard function go to zero in this limit, but we might hope that the ratio approaches a finite value, and we might further hope that this finite value would equal the steady-state closed-loop hazard rate. Now, there are good reasons for expecting the ratio to approach a finite value, but there is no particular reason to think this asymptotic value will equal the steady-state closed-loop hazard rate in general. Indeed we can show that, in general, it does not, although it happens to be approximately equal in some cases.

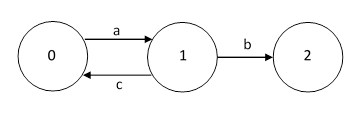
Consider the simple 3-state model shown below.

The equations of state are

The roots of the characteristic equation r² + (a+b+c) r + (ab) = 0 are eigenvalues of the system, so we have

If every widget entering State 2 is repaired and returned to State 0, then this is really a closed loop system, and the hazard rate for State 2 is exactly

(See Open Loop and Closed Loop Markov Models for a derivation of this result.) If, on the other hand, we decide to treat this as an open loop model, allowing all probability to eventually accumulate in State 2, what is the asymptotic hazard rate for State 2? Taking P₀(0) = 1 and P₁(0) = P₂(0) = 0, we solve the equations of state explicitly to find that the probabilities of the three states at the time t are

Therefore, the hazard rate for State 2 as a function of time is

Writing the characteristic roots as r₁ = α + β and r₂ = α – β where β is positive this becomes

As t increases the second terms in the numerator and denominator go to zero, so the asymptotic rate is

(Note that, according to our sign conventions, r₁ is the small of the two roots.) This is not the same as the true steady-state hazard rate, which is λ₂ = ab/(a+b+c), although it will be close if the transition rates a,b are small compared with c. To prove this, we can factor the right hand expression

The fractional term under the square root is always less than 1 (for positive values of a,b,c), so the binomial series for the square root converges. Thus we have

This explains why the asymptotic hazard rate for the open loop model (for this very simple system) tends to be comparable to the actual steady-state hazard rate ab/(a+b+c) of the closed loop system. However, the convergence of this series is not very rapid unless c is much greater than a or b, so the discrepancy can be noticeable. For example, with the transition rates a = 0.01, b = 0.02, and c = 0.005 the steady-state system has a hazard rate of 0.00571 whereas the asymptotic rate for the open loop model is 0.00719. If we define the ratios α = a/c and β = b/c then the asymptotic rate can be written as

The coefficients 1, 1, 2, 5, 14, … are the Catalan numbers. This shows that the asymptotic open loop rate (for this simple model) can be made to approach the closed loop rate by making either a/c or b/c sufficiently small. Also, the asymptotic open loop rate is always greater than the closed loop rate. Incidentally, the time T at which will λ_2,open(T) exactly equals λ_2,closed can be found by equating the two exact expressions and solving for T, which gives

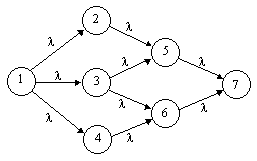
For another example, consider the Markov model shown in the figure below.

In another article the explicit formula for P₇(t) was found to be

so the hazard rate for State 7 is

which obviously approaches λ in the limit as t approaches infinity. On the other hand, the closed-loop steady state solution for this system is given by solving the system

which gives the result

Thus the hazard rate for State 7 is

which is just 6/13 of the asymptotic open-loop rate.

In general, for any Markov model, the asymptotic open loop rate is always equal to the negative of the dominant eigenvalue, where "dominant" means the smallest absolute value. This is because the time-dependent probability for the shutdown state (assuming n distinct eigenvalues) is

where r₁, r₂, ..., r_n are the eigenvalues of the homogeneous system, and c₁, c₂, ..., c_n are some non-zero coefficients. (We require non-zero coefficients to exclude cases in which the model structure or initial conditions make P(t) independent of one or more of the terms.) Therefore, the time-dependent rate is

The eigenvalues are all negative, so as t increases to infinity the numerator and denominator both become dominated by whichever exponential shrinks most slowly, i.e., whichever term has the smallest magnitude of eigenvalue. For example, if r₂ is the smallest eigenvalue, then the rate approaches

Thus the asymptotic open loop rate is just the negative of the smallest eigenvalue of the homogeneous system. (This derivation assumed distinct eigenvalues, but even if the system has repeated roots we can carry through essentially the same derivation to show that the asymptotic rate is still the negative of the dominant eigenvalue.)

Of course, the asymptotic rate of the open loop system does not generally equal the asymptotic rate of the closed loop system. As shown in the note on Two Properties of Markov Models, the latter is given by

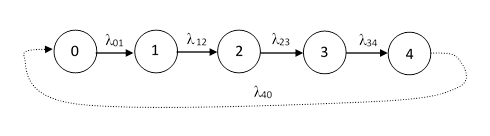
where I is the identity row vector, U_j is the unit column vector formed by scaling the jth column of the coefficient matrix (omitting the jth row), and m is the homogeneous coefficient matrix. To show that the open and closed loop rates can differ by arbitrarily large amounts, consider the series system shown below.

The full transition equation for this system is

The homogeneous system has the eigenvalues –λ₀₁, –λ₁₂, –λ₂₃, –λ₃₄ , so the asymptotic open loop rate for State 4 is the smallest of these eigenvalues. On the other hand, the asymptotic closed loop solution is given by setting the matrix m equal to the coefficient matrix with the 4^th row and column deleted, and by setting U₄ to the last column with the last element deleted and normalized to a sum of unity. In these terms λ₀₄ is given by

If we let T_ij denote the mean time for the system to pass from State i to State j, then it’s intuitively clear that

and this corresponds to the fact that

In contrast, the reciprocal of the asymptotic open loop rate is just the maximum of the four individual values 1/λ₀₁, 1/λ₁₂, 1/λ₂₃, and 1/λ₃₄, which obviously doesn’t represent the mean time from State 0 to State 4. This can be as much as a factor of 4 less than T₀₄. For higher-order systems there is no upper bound on the possible ratio of the asymptotic rates for the open and closed loop systems.

It might seem that the asymptotic condition of the open loop model would be with all the probability that is not in State 4 concentrated in State 3, which could lead us to suspect that the asymptotic rate ought to be λ₃₄, regardless of whether this is the smallest of the rates. However, the asymptotic condition actually tends to establish a disproportionate fraction of the probability in the state with the lowest exit rate, so the lowest rate tends to dominate the result. In view of this, we might suspect that the asymptotic rate should therefore be somewhat less than the smallest transition rate, because once the system makes this transition it must still traverse the remaining states before arriving at State 4. But in fact the presence of probability in the downstream states, with their greater transition rates, exactly compensates for this, leading to the interesting result that the normalized asymptotic rate for entering State 4 is precisely equal to the lowest of the individual upstream transition rates, no matter how far upstream that rate occurs.

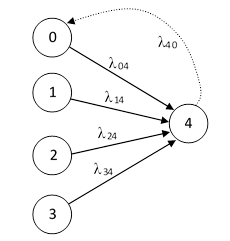
Another system whose eigenvalues equal the individual transition rates is the parallel model shown below.

The full transition equation for this model is

Similar to the previous model, the homogeneous system for this model has the diagonal eigenvalues –λ₀₄, –λ₁₄, –λ₂₄, –λ₃₄ , so the asymptotic open loop rate for State 4 is the smallest of these eigenvalues. (Naturally this assumes some non-zero initial probabilities for each of the states 0 to 3.) For this model the result is quite intuitive, because eventually almost all the probability that is not in State 4 will be in the state with the lowest transition rate, so that will be the asymptotic rate of transition into State 4. On the other hand, the closed loop model gives an asymptotic rate of

as expected, since State 0 is the only state with feedback from State 4.

Return to MathPages Main Menu