Reversibility and Entropy

A certain professor of thermodynamics was known to give the same final exam every year, always consisting of just the single question:  “What is entropy?”  One day an assistant suggested that it might be better to ask a different question now and then, so the students wouldn’t know in advance what they would be asked.  The professor said not to worry.  “It’s always the same question, but every year I change the answer.”

The defining characteristic of a reversible process is that it can (or could) proceed equally well either in the forward or the reverse temporal directions.  An irreversible process is one that can only proceed in one temporal direction, and would violate the laws of physics if it proceeded in the reverse time direction.  At first this might seem to be a reasonable and unproblematic classification, since we can easily think of physical processes that are (essentially) reversible, such as the progression of the planets in orbit around the sun, and we can also think of processes that are (evidently) irreversible, such as the expansion of a gas released into a room from a small container.  In the case of the planetary orbits, if we filmed the solar system and then played the film in reverse, the orbital motions would still look physically realistic, i.e., they would still satisfy Newton’s laws, for the simple reason that Newton’s laws are time-symmetric (neglecting tidal effects and not considering gravitational waves).  In contrast, if we filmed the expanding gas, and then ran the film in reverse, the behavior would look highly unrealistic, as all the wisps of gas backed out of the room and converged, finding their way back into the small container.

However, if we consider the case of the expanding gas more carefully, a puzzle arises.  On the molecular level the gas can be regarded as consisting of many individual particles, each of which obeys Newton’s laws of motion, which, as already mentioned, are time-symmetric.  The individual trajectories of these particles, including the effects of their perfectly elastic collisions, are therefore reversible, so the entire process of the gas expanding into the room must also be reversible, in the sense that it would not strictly violate any fundamental laws of mechanical dynamics.  In fact, all the fundamental laws of physics are purely time-symmetric, including the laws of electromagnetism and the wave equation of quantum mechanics.  (This is indirect evidence of inherent temporal asymmetry in one particular decay process in quantum mechanics, but this decay plays no role in most physical processes, so it cannot account for irreversibility.)  The puzzle is how seemingly irreversible processes emerge from the workings of purely reversible phenomena.  Perhaps it’s better to ask what exactly we mean by “irreversible”.

A solid object moving at constant speed in a straight line through the vacuum of empty space from point A to point B may be regarded as a very simple reversible process.  If we reverse the direction of time, the process consists of the object moving at constant speed in a straight line from B to A.  If instead of a vacuum we imagine the object immersed in a highly viscous (and initially static) fluid, it might begin at point A with some speed and direction of motion, but would quickly lose speed, and arrive at point B moving very slowly.  Reversing the direction of time for this process, we begin with a slowly moving object at B, which then accelerates toward A, and arrives at A with increased speed.  This reversed process seems unrealistic, but it need not be, provided both the object and the fluid are given the correct initial conditions, i.e., the time-reversal of the final conditions that existed once the object had moved from A to B.  The reason the accelerating object seems so unrealistic is that it would be practically (but not theoretically) impossible to set up the appropriate initial conditions in the fluid and surrounding container. 

Of course, it’s quite easy to set up the reverse of the required conditions, simply by beginning with a stationary fluid and then pushing the object from A toward B.  At the end of this process, when the object arrives (slowly) at B, we will have the reverse of the required initial conditions for the unrealistic process, but actually reversing them is far from trivial.  This is presumably what Boltzman had in mind when someone criticized his derivation of the second law on the grounds that any process which occurs is necessarily reversible by simply reversing the conditions at the end of the process, and he answered “Go ahead and reverse them”.  The point being that it’s not so easy. 

If we touch the center of a pool of water, we can produce a circle of ripples emanating outward.  The laws of mechanics governing the propagation of these waves are time-symmetrical, so in principle it would be possible to arrange for in-coming ripples to converge on a point in the center of the pool.  However, this would require a perfectly coordinated set of initial conditions at the boundaries of the pool, something which is practically impossible to accomplish.  Furthermore, to leave the pool in its quiescent state, it would be necessary for a finger to come into contact with the water exactly as the waves converged to absorb the momentum.

These example suggest that our intuitive sense of what processes can and cannot realistically occur depends to a great extent not just on the fundamental physical laws but also on the degree of coordination in the boundary and initial conditions necessary for the process to occur.  Thus, even though every process is theoretically reversible, we may legitimately regard a process as irreversible if the process would require a sufficiently high degree of coherence and coordination in the boundary conditions.  However, even this approach doesn’t lead to a completely satisfactory representation of irreversibility. 

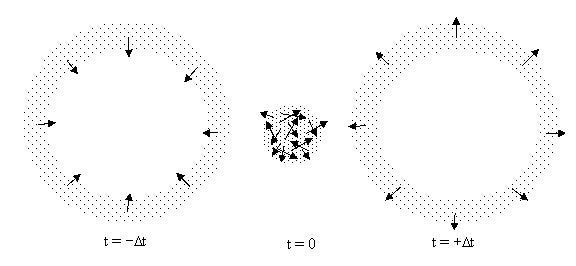
To see why, consider a collection of particles distributed at random inside a spherical region of empty space.  We’ll assume the particles are point-like, so they don’t interact.  If the particles are all stationary, the configuration will remain unchanged, but suppose each particle has a speed v in a randomly chosen direction.  After some time has passed, the volume of the minimum convex region enclosing the particles has necessarily increased, because some of the particles on the original outer perimeter had outward velocities.  In fact, it’s easy to see that, after a sufficient amount of time, the particles will occupy an expanding spherical shell whose thickness equals the diameter of the original sphere, as shown below.

Hence beginning from a “random” bounded configuration of particles there is a tendency for the particles to disperse and expand into the surrounding space, and we might be tempted to regard this as proof that “most” configurations tend to disperse in the positive time direction.  However, just as we can extrapolate the future positions of the particles from their initial positions and velocities, we can also extrapolate their positions into the past, and when we do this for our sphere of randomly directed particles we find that it expands into the past exactly as it does into the future.  Snapshots at three consecutive instants are shown below.

The “randomness” of the directions of motion at time t = 0 corresponds to the fact that, at this instant, the configuration is a superposition of all the incoming spherical regions.  As the particles expand into the future or the past, they tend to “sort themselves out”, because all the particles with a given direction of motion end up in the same spatial region.  In a sense, we could say the overall “orderliness” is conserved, because as the particles become more spatially concentrated (increasing the correlation between their positions), the correlation between the directions of motion of neighboring particles is reduced.  This conservation isn’t surprising, because we stipulated that the particles don’t interact.  However, if we give the particles some non-zero cross section and allow them to bounce off each other, the boundaries of the expanding shell would not be as sharply defined, but we would still have a time-symmetric situation, with a spherical cloud of particles converging inward from the past and then expanding outward into the future.

The second law of thermodynamics is closely related to the idea of an irreversible process, and it is perhaps the only fundamental law of physics that is asymmetrical with respect to time.  In fact, it has been argued that the second law is an essential aspect of the meaning of time itself.  The law can be expressed in many different (but equivalent) ways.  One statement is that heat always flows from higher to lower temperature, never from lower to higher.  Another statement is that it’s not possible for any cyclic process to convert heat entirely into work.  To formalize statements of this kind in a more general and quantitative way, a state variable called entropy is defined, and the second law is expressed by saying that the overall entropy (of an isolated system) can never decrease.  It follows that a process in which entropy increases is irreversible.

So, the meaning of “irreversibility” is intimately connected to the meaning of the thermodynamic quantity called entropy.  Historically there were two different approaches to defining entropy.  Originally it was defined as a macroscopic state variable in the context of classical thermodynamics.  Later it was defined in terms of kinetic theory and statistical mechanics.  What exactly is entropy?  Recall that the first law of thermodynamics asserts that energy can neither be created nor destroyed, so the total amount of energy in the universe is constant, and yet when we use energy to perform some task there is a sense in which that energy has been “expended”.  The ability of energy to produce change depends on the unevenness with which the energy is distributed.  If everything in a system is in equilibrium, no change can occur, despite the fact that there may be a large amount of energy in the system.  In a sense, entropy is a measure of the uniformity of the distribution of energy.  The second law of thermodynamics tells us that energy tends to become more uniformly distributed.

How should we quantify the concept of uniformity?  Suppose we distribute ten balls into ten urns.  Assume for the moment that each urn and each ball is individually distinguishable.  Now, the least uniform distribution would be for all ten balls to be in just one of the urns, leaving the other nine urns empty.  Assuming the arrangement of balls within a given urn is of no account, there are 10 distinct configurations of the system such that all ten balls are in just one of the ten urns.  At the other extreme, the most uniform arrangement would be for each urn to contain exactly one ball.  In this case we have ten choices for the placement of the first ball, nine choices for the placement of the second, and so on, giving a total of 10! = 3628800 distinct configurations with this perfectly uniform distribution.  In general, we find that there are many more distinct ways for the elements of a system to be distributed uniformly than there are for it to be distributed non-uniformly, so we take this as the basis of our definition of entropy. 

We might simply define the entropy of a given distribution as being proportional to the number N of distinct ways in which that distribution can be realized (within the constraints of the system).  However, if we did this, the total entropy of the union of two similar isolated systems considered as a single system would be the product of their individual entropies, because the two constituent systems are still regarded as distinct, so each of the N₁ possible arrangements of the first system in its distribution could be combined with each of the N₂ possible arrangements of the second system in its distribution, giving a total of N₁∙N₂ distinct ways of realizing the joint distribution.  It’s more convenient to define entropy in such a way that the total entropy of the union of two systems is the sum of their individual entropies, because this enables us to regard entropy as an intrinsic property.  To accomplish this, recall that the logarithm of a product equals the sum of the logarithms of the factors.  Thus if we define the entropy of a distribution with N possible realizations as S = k ln(N), where k is just a constant of proportionality, then the entropies of the two system distributions in our example are S₁ = k ln(N₁) and S₂ = k ln(N₂), and the entropy of the union of these two distributions is

In the above discussion we’ve glossed over some important points.  First, we should point out that we have not actually defined the entropy of a system, we have defined the entropy of a distribution of the elements of a system.  Moreover, we’ve assumed that many distinct configurations of the system represent realizations of the same distribution.  For example, the configuration of having all ten balls in the first urn is regarded as being the same distribution as having all ten balls in the second urn, or all in the third, etc., even though these are counted as ten distinct configurations.  When we count configurations we treat each ball and each urn as individually distinguishable components, but we abstract away most of this distinguishability when we define the distributions.

We assumed in the above discussion that the arrangement of balls within a given urn was of no account, but suppose instead we assume that each urn is a tube, and the balls are placed in the urn in a definite linear order.  In this case there would be 10! distinct ways of placing ten distinguishable balls into any single urn.  On this basis we would have to conclude that there are 10∙10! distinct ways of having all ten balls in any one of the ten urns, whereas there are still only 10! distinct ways of having exactly one ball in each urn.  This seems to suggest that the non-uniform distribution has higher entropy than the uniform distribution.  However, the imposition of a definite sequence in the arrangement of the balls in an urn represents a new constraint, and it implies that the positioning of each balls is not independent of the others.  The balls must be placed in a certain sequence (because we do not have a 10x10 array, we have a 10-place array with a fixed sequence for multiple entities in each position).  If we fix this sequence, there are still 10! ways of producing the uniform distribution, but only 10 ways of producing the most non-uniform distribution.  This shows that there are some conceptual difficulties involved in the determination of the number of “distinct arrangements” in which a given “distribution” can be realized. 

Often we refer to the individual distinct arrangements of a system as microstates, and to the distributions of the system as macrostates.  Then we say the entropy of a given macrostate is proportional to the logarithm of the number of microstates covered by that macro-state.  Notice that we count each microstate as being equal, i.e., each microstate contributes exactly one to the total number of microstates.  We don’t try to assign different “weights” to different microstates.  As long as it is a distinct arrangement from any of the other microstates, it counts as a full fledged microstate.  It isn’t a priori obvious that every microstate is created equal, but we take this as assumption.  Of course, this simply pushes the issue back onto the question of what constitutes distinctness.

In statistical mechanics the concept of entropy was first developed in relation to ideal gases.  In this context we can consider a fixed number n of gas molecules, and the 6n-dimensional phase space for this system, representing the components of the position and momentum of all the molecules.  The state of the system, then, is represented by a single point in this phase space.  To define the entropy of a given macrostate of this system we partition the phase space into regions that correspond to the distinguishable macrostates, and then count the number of microstates contained within the given macrostate.  There is admittedly a degree of arbitrariness in defining the boundaries of the macrostates, because the distinction between macro and micro is somewhat subjective.  We could regard each microstate as a macrostate, and then the entropy of every state would be zero.  The concept of entropy works best and is most useful when there is a “thermodynamic limit” in which aggregate “state properties” such as temperature and pressure are applicable.

The regions corresponding to highly uniform distributions of energy are very large - many orders of magnitude larger than regions corresponding to non-uniform distributions - so as the system meanders around in phase space it almost certainly will be found in progressively larger and larger regions, i.e., macrostates of higher entropy.  However, we still encounter the puzzling fact that the same argument works in reverse time.  If we extrapolate the same meandering pattern backwards in time, we always would expect the entropy to have been decreasing up to the present moment, and then increasing toward the future.  Since in fact the entropy of the world has been increasing in the past leading up to the present moment, we are forced to conclude that the “meandering” of the system in phase space is not temporally symmetric.  But all the classical laws of physics are temporally symmetric, so we still face the question of how a system whose detailed behavior is governed by symmetrical laws can evolve in such an asymmetrical way.

Many ideas have been proposed to resolve this puzzle, mostly of two general types.  It can be argued that the second law of thermodynamics is explained by the fact of extremely low entropy in the past, and so the task becomes to explain why the universe began with such low entropy.  Alternatively, it can be argued that the fundamental laws of physics are not temporally symmetric after all, but embody some fundamental directionality, despite their apparent reversibility.  For example, Ritz argued that Maxwell’s equations were flawed because they permit advanced as well as retarded wave solutions, yet we never observe advanced waves.  More fundamentally, the measurement process in quantum mechanics can be seen as irreversible, even though the relativistic Schrodinger equation is time-symmetric.  Whatever the case, it clearly is not correct to extrapolate the state of a system backwards in time symmetrically with our extrapolation forward in time, because this leads unavoidably to the implication of greater entropy in the past.  It must be that either there is a temporal asymmetry in the physical laws or else there is an asymmetry in the current conditions, such that extrapolation backwards in time leads to conditions of progressively lower and lower entropy.  If the laws are symmetrical, and the difference between the forward and backward behavior can be attributed entirely to the asymmetric state of the present condition, then this seems to imply nearly perfect precision in order for the backward trajectory to continue to find itself in states of lower and lower entropy.

Incidentally, we sometimes see a more generic definition of entropy, based explicitly on probability.  Let a given macrostate consist of N microstates, and let p_j denote the probability of being in the jth microstate (on condition that the system is in the given macrostate).  Then the entropy of this macrostate can be defined as

Notice that if a macrostate consists of N equally probable microstates, then p_j = 1/N for all j, and so the summation reduces to S = k ln(N), just as before.

Since probabilities and logarithms are dimensionless, the constant of proportionality k (Boltzman’s constant) determines the units of entropy.  For consistency with the use of entropy in thermodynamics, the value of this constant is taken to be R_u/N_A where R_u is the universal gas constant and N_A is Avogadro’s constant.  Thus we have k = 1.380E-23 Joules/[deg K molecule].

Return to MathPages Main Menu