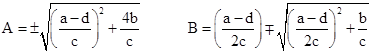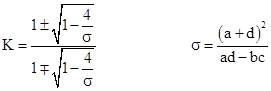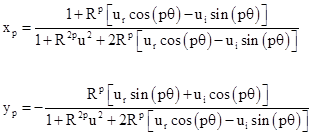Is Entropy Quantized?

It’s well known that the entropy of a system is invariant under Lorentz transformations. This was first discussed by Max Planck in a paper entitled “On the dynamics of moving systems” in 1907. His reasoning was remarkable simple. Considered a body initially at rest relative to inertial coordinate system Σ, and then accelerated by a reversible adiabatic process so that it comes to rest relative to a different inertial coordinate system Σ′. If we let η₁ and η₂ denote the entropy of the body in these two states of motion relative to Σ, then we have η₁ = η₂ because the process is reversible. Likewise, letting η₁′ and η₂′ denote the entropy of the body in these same two states of motion relative to Σ′, we have η₁′ = η₂′. Now, if the entropy of a body is larger relative to a system of coordinates in which it is moving than relative to a system in which it is at rest, then we have η₁′ > η₁, and also η₂ > η₂′. But substituting η₁ and η₂′ in place of η₁′ and η₂ respectively in the latter relation we get η₁ > η₁′, which contradicts the former relation. Hence η₁ = η₁′. Of course, this reasoning assumes that the acceleration of the body can be carried out in a reversible adiabatic way, but this is fairly unobjectionable.

Occasionally one sees an even simpler argument for the invariance of entropy. It is asserted that the entropy of a system (in a given macro-state) is proportional to the logarithm of an integer, namely, the number of distinguishable divisions of its energy content. This, of course, is just the fundamental definition of entropy. Now, since Lorentz transformations are continuous, and since entropy can only change discontinuously, it follows that entropy must be invariant under Lorentz transformations. On the other hand, some people object to this line of reasoning, claiming that the entropy of a system need not be (proportional to) the logarithm of an integer. They point out that if a system is in a macro-state corresponding to n possible micro-states, and the probability of it being in the ith micro-state is p_i, its entropy is

which, they claim, needn't be the logarithm of an integer. However, this summation can vary continuously only if the individual p_i are assumed to be continuously variable, which is an invalid assumption for a finite-state system.

This is an interesting argument. Classically the size of an micro-region (or "cell") in phase space was somewhat arbitrary, the only criteria being that it should be small enough so the changes in energy from one cell to the next were small, and yet large enough to contain a statistically significant population of particles. This is a vague and not very satisfactory foundation, and it is basically the reason for the initially arbitrary constant "k" in the formula S = k log(W). Quantum mechanics gives a much clearer and more definite picture, since the smallest size of a cell in phase space is a multiple of the irreducible spacing between allowable energy levels, which explains why h³ shows up in so many expressions for the volume of a phase cell. On this basis Planck and others were able to derive expressions for the absolute entropy of a system, removing the arbitrariness of "k". Planck later wrote that it was the determination of the value of Boltzman’s constant, rather than the results on black-body radiation, that convinced him of the fundamental importance of energy quantization and the constant h.

If we accept that the allowable energy states of a system are quantized (with a granularity on the order of Planck's constant), then there is a sense in which entropy does indeed change discretely, since for any process we have

where n is the total number of particles, n_i is the number of particles in the ith energy level, N is the number of energy levels, and

where U is the total energy of the system, E_i is the energy of the ith (quantized) energy level. Now, the value of W in (1) commonly refers to the most probable macro-state, but we could consider all the macro-states if we wish, and it wouldn't affect the question of whether entropy is ultimately a continuous or a discrete quantity. Typically we make various macroscopic approximations to (1), introducing the temperature variable, and arrive at something like

Now, since the sum in this expression is the internally reversible change in heat, we have the familiar relation dS = (dQ/T)_rev. Thus, to the approximation that thermodynamic temperature is a continuous variable, so too is entropy. However, "temperature" is inherently a macroscopic parameter, not really suitable for describing the state of individual particles, nor is it accurate on the scale of Planck's constant. If we examine the entropy closely enough, it is indeed discrete, although the granularity is incredibly small for typical macro-systems.

There is, however, another possible objection to the proposed "proof" of entropy invariance under Lorentz transformations. Even if it is granted that the allowable entropy levels are (on some level) discrete, we can question the assumption that the allowable Lorentz transformations are perfectly continuous. Of course, the usual equations expressing the general form of a Lorentz transformation are continuous, but it isn't obvious that the physically allowable Lorentz transformations are actually continuous, at least not on the scale of Planck's constant. In fact, any demonstration that they are continuous on this scale would seem to be ruled out by the uncertainty principle. Hence we can’t legitimately appeal to the continuity of allowable Lorentz transforms to "prove" that entropy is invariant under those transformations.

By the way, these ideas have been explored quite a bit, especially by people (e.g. Penrose) trying to see if the divergences that arise in various field theories are in some sense due to the assumption of infinitely divisible continuous Lorentz transformations, somewhat analogous to the ultra-violet catastrophe based on the assumption of continuous energy levels. There are some mathematically interesting ways in which Lorentz transforms can be quantized, particularly from the standpoint of the complex matrix representation and the associated Mobius transformations of the complex plane under stereographic projection. When represented in this way, it seems natural for the Lorentz transformations to be discrete, i.e., z → (az+b)/(cz+d) for some fixed complex numbers a,b,c,d (with ad–bc = 1). Of course we can parameterize this to act continuously, but the continuous forms are quite algorithmically complicated in comparison with the extreme simplicity of the discrete transforms. It might be interesting to figure out how the coefficients of Mobius/Lorentz transformations might have to be restricted in order to be consistent with discrete entropy changes from one "allowable" inertial frame to another, although this would probably be tricky, especially since the accomplishment of any Lorentz transformation involves an acceleration, during which the invariance of entropy is more problematic.

Note that continuous and discrete changes can both be represented equally well in the spacetime domain as Lorentz transformations or on the extended complex plane as Mobius transformations. Those aren't two different ways of analyzing the same thing, they are two ways of analyzing two different things (continuous and discrete transitions). However, in the Mobius domain the discrete transformations happen to be more natural. The explicit continuous parameterization of a general Mobius transformation is much more complex than the corresponding discrete recursive formula, which is simply

This generates the discrete sequence f₁(z) = f(z), f₂(z) = f(f(z)), f₃(z) = f(f(f(z))), and so on for all f_n(z) where n is a positive integer. Now, if we want to apply this transformation continuously as a function of the real parameter p (instead of the integer parameter n), we must (in general) first map this to a domain in which the conjugate transformations have some pure exponential form, apply the pth-order transformation, and then map back to the original domain. In the most general case with c ≠ 0 and (a–d)² ≠ –4bc the continuous function f_p(z) is given by

where

with

To explicitly give the real and imaginary components of z_p = x_p + i y_p under just the action of F (leaving aside the conjugacy braces), let K = Re^iq , and define

Then the components of z_p are

Clearly this continuous form of F, to say nothing of H^–1FH, is far more algorithmically complicated than the general discrete recursive form (az+b)/(cz+d). The reason for the difference is that we can evaluate the discrete form recursively, whereas the continuous form can only be implemented explicitly. This is why the continuous form of a general Mobius transformation involves more complicated expressions and is substantially more algorithmically complicated than the recursive discrete forms. When applying the criteria of conceptual simplicity to explanations of the workings of nature, the difference in algorithmic complexity between explicit continuous transforms and recursive discrete transforms is not inconsiderable.

Regarding the finite subgroups of Mobius transformations, note that for any given n there are, up to conjugacy, ϕ(n) distinct Mobius (and therefore Lorentz) transformations with fundamental period n, where ϕ(n) is Euler's totient function. Each of these (necessarily elliptic) transformations generates a cyclic group of order n. These would presumably have to be augmented by some suitable discrete transforms of one or more other type(s) in order to generate (approximately) the full set of Lorentz transformations. 

Return to MathPages Main Menu