|
Wonder En Is Gheen Wonder |
|
|
|
It is the task of science to reduce mysteries to trivialities. |
|
Niels Bohr |
|
|
|
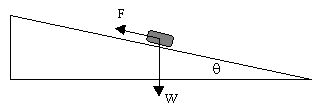
In 1586 the Dutch scientist and civil engineer Simon Stevin published a book on mechanics in which he derived the law of forces for inclined planes, and more generally the vector law for the decomposition of forces. His derivation is interesting because it's one of the first clear examples of a law of mechanics being deduced from a general physical principle, namely, the conservation of energy. The problem was to determine the force F required to hold a frictionless object (of known weight W) in place on an inclined ramp, as shown below. |
|
|
|
|
|
|
|
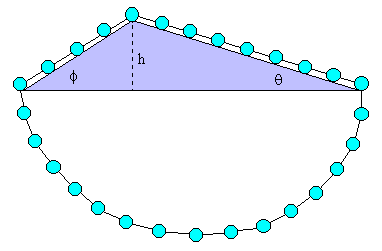
This seems like a trivial problem today because we take the rule for the decomposition of forces for granted, but Stevin was the first to derive this rule. His approach was to consider two inclined planes, back-to-back, with a loop of beads placed on them as shown below. |
|
|
|
|
|
The beads are evenly spaced around the entire loop (clootcrans, or "wreath of spheres"), so the number of beads nL on the left hand slope is proportional to the hypotenuse h/sin(ϕ) and on the number of beads nR on the right hand slope to the hypotenuse h/sin(θ). Thus we have the relation |
|
|
|
|
|
|
|
The beads beneath the planes are symmetrically arranged, so they pull equally in both directions. Therefore, the beads on top of the planes must also pull equally in both directions, because we know the loop will be stationary, i.e., it will not be a perpetual motion machine. If we set ϕ equal to 90 degrees, the pull of the left-hand beads is just the weight W of each bead times the number of beads, which is proportional to h. This must equal the pull of the right-hand beads, of which there are h/sin(θ), so if we let F denote the force of gravity on each bead parallel to the inclined plane, we have the relation Fh/sin(θ) = Wh, from which we get |
|
|
|
|
|
|
|
To find the force exerted by each bead perpendicularly into the inclined plane surface, notice that we can consider the dual situation in which the string is constraining the bead to move along an "inclined plane" perpendicular to the string. In this case the inclined plane has an angle θ′ = π/2 - θ, and the force is W sin(θ′) = W cos(θ). This can all be illustrated in the figure above if we make the apex a right angle by choosing θ + ϕ = π/2. This is how Stevin derived the fact that the component of a force in any particular direction is simply equal to the projection of that force vector onto the direction axis. For orthogonal coordinate systems we can express any total force Ft making an angle θ with the x axis as the vector sum of the basis components |
|
|
|
|
|
|
|
Stevin was quite fond of this demonstration, and underneath the figure he wrote "Wonder en is gheen wonder" (what appears a wonder is not a wonder), a saying that conveys how the sense of mystery and wonder is dispelled by the clear understanding given by the clootcrans thought experiment. |
|
|
|
The most interesting thing about this derivation is that it was a thought experiment, viz, Stevin didn't assert that the loop of beads had been shown empirically to be stationary in every possible case, he asserted that the forces obviously must balance, because otherwise it would constitute a perpetually imbalanced force, i.e., a perpetual motion machine, which is impossible in principle. Thus Stevin's derivation is based directly on the principle of energy conservation - even though this principle was not formally articulated (for mechanics) until a century later. |
|
|
|
Simon Stevin (1548-1620) is most widely remembered today for promoting the use of decimal fractions, which led directly to modern decimal notation, but he actually wrote influential works on a variety of subjects. In the field of astronomy he was one of the first proponents of the Copernican system. He also observed (before Galileo) that bodies of differing weights all fall a certain distance under the influence of gravity in the same time. He also wrote on hydrostatics, optics (perspective), algebra, and the design of military installations. |
|
|
|
Incidentally, Stevin's collected works were translated into Latin and published in 1608 by Willebrod Snell, who subsequently discovered the law of refraction, namely, |
|
|
|
|
|
|
|
where ni and nt are the indices of refraction and θi and θt are the angles of incidence and transmission. The formal similarity between this law and Stevin's equation for the number of clootcrans beads on the ramps is presumably just coincidental, but it's still interesting how some simple mathematical forms reoccur in different contexts at about the same time. |
|
|