Pappus' Theorem
Pappus of Alexandria was a Greek mathematician who lived around the end of the third century AD, although the exact date is uncertain. Theon made a marginal note in one of his manuscripts stating that Pappus wrote during the reign of Roman emperor Diocletian, which places him in the period from 284 to 305 AD, but it also seems from Pappus' commentary on Ptolemy's Almagest that he witnessed a particular solar eclipse that occurred in 320 AD In any case, the "Collection" (Synagoge) of Pappus is an invaluable source of information on Greek mathematics, since it contains summaries and attributions of results based on ancient works that have subsequently been lost. In addition, Pappus gave some apparently original results, such as the proposition that is commonly called "Pappus' Theorem" involving a hexagon inscribed between two lines.
Consider two straight lines emanating from point O and containing the points P1 through P6 as shown in the figure below.
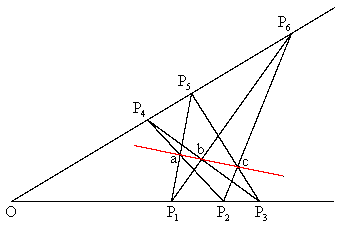
Letting Lij denote the line through points Pi and Pj, and letting a,b,c denote the points of intersection between the pairs of lines [L15,L24], [L16,L34], and [L35,L26] respectively, Pappus' Theorem asserts that the points a,b,c lie on a straight line.
An explicit analytical demonstration of this theorem by determining the coordinates of the points a,b,c is straight-forward, but algebraically less trivial than one might expect. Let xi,yi denote the coordinates of the point Pi, and note that yi = 0 for i = 1,2,3 and yi = kxi for i = 4,5,6 where k signifies the slope of the line OP6. (We have drawn the line OP3 along the x axis for convenience, but we can obviously rotate the entire figure without affecting the co-linearity of any set of points.) The coordinates xa,ya of point a satisfy the conditions
![]()
Solving these for xa and ya gives
![]()
If we let ui denote 1/xi we can re-write these coordinates as
![]()
Similarly the coordinates for points b and c can be written as
![]()
![]()
We can also write these coordinates in the form
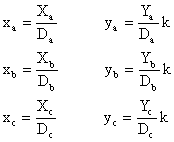
where
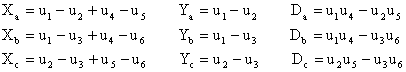
Notice that
![]()
Now, the condition of co-linearity for the points a,b,c is
![]()
which can be re-written in the form
![]()
(We have divided through by k.) The numerators are equal to each other, because the relation
![]()
can be re-arranged into the form
![]()
and, by relations (1), the quantities in parentheses equal Yb and Db respectively. Likewise the denominators of (2) are equal to each other, so the co-linearity condition is satisfied.
It's interesting that, when expressed in terms of numerators and denominators as shown above, xb is the mediant xa and xc, just as yb is the mediant of ya and yc. So, in a literal sense, the point b is the mediant of points a and c. In other words,
![]()
This enables us to encode number-theoretic propositions involving Farey sequences in geometrical form, because the successive terms of a Farey sequence are the mediants of the two preceding terms.
It's also worth noting that the original points need not be arrange on two lines in the order shown on the previous figure, and the points of intersection need not fall between the two original lines. The figure below illustrates another configuration, one for which the line of intersection points falls outside the two original lines.
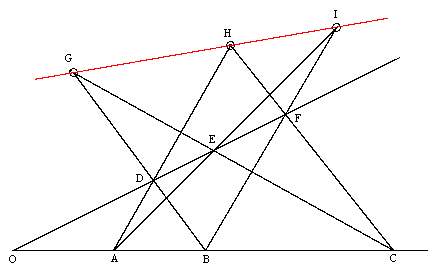
The usual method of proving Pappus' Theorem today is in the context of projective geometry. Given any figures drawn on a flat plane surface S, we can imagine this plane embedded in three-dimensional space, and we can select an arbitrary point P in the space (not on S) and some other flat plane surface S', and we can project (map) every point p of S uniquely to a point p' of S' such that P, p, and p' are colinear. It's clear that straight lines on S map to straight lines on S'. The only possible exception is that, since S and S' are not in general parallel, there is a line on S such that the projection ray from P through this line is parallel to S', and therefore never intersects with S' (in either direction). To remedy this, we augment each plane with a "line at infinity". Since every pair of lines intersects at a single point, we must stipulate that the intersection of any given line with the line at infinity is a single point, regardless of the direction along the line.
Now, given any plane figure such as the one shown above, we can project it onto another plane in such a way that the line through the points G and I is mapped to the line at infinity, and then we wish to show that H is also on the line at infinity. If we can show this, then it proves that H was colinear with H and I in the original plane as well (since any projective mapping preserves straight lines). In the projected plane S', if G' is on the line at infinity, then the intersecting lines B'D' and C'E' must be parallel. Likewise if I' is on the line at infinity, the intersecting lines A'E' and B'F' must be parallel. Therefore, the projected figure is as shown below.
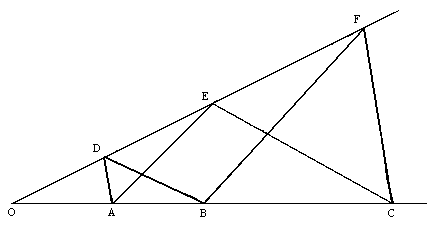
where the symbols A,B, etc., denote the projected versions of those points. By similar triangles we have
![]()
Multiplying through these expressions by OE and OB respectively, and taking the ratio, we get
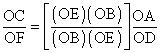
Obviously the quantity in square brackets is unity, because multiplication of real numbers of commutative, which is to say, xy = yx. Therefore, OAD and OCF are similar, so AD and CF are parallel, which proves that their point of intersection (the point H) is on the line at infinity, co-linear with the points G and I.
It's worth noting that Pappus' Theorem relies on the commutivity of multiplication of lengths. Needless to say, the previous proof freely also made use of commutative multiplication of lengths. We could imagine a geometry in which this does not apply, and in such a context Pappus' Theorem would not be valid.
About 1300 years after Pappus wrote the Collection, an interesting generalization of Pappus' Theorem was discovered by Blaise Pascal based on the ideas of Girard Desargues. This generalization is discussed in the note on Pascal's Mystic Hexagram.