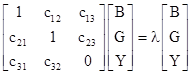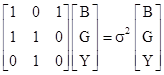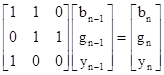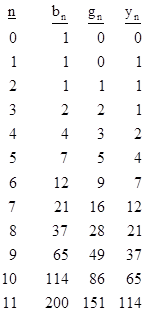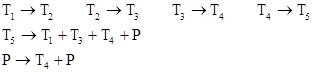Tilings Based on Perrin's Sequence

Perrin's sequence consists of the integers 3, 0, 2, 3, 2, 5, 5, 7, 10,... and so on, satisfying the recurrence relation s_n = s_n−2 + s_n−3. We wish to construct a non-periodic tiling of the plane with the corresponding characteristic polynomial p(x) = x³ − x − 1. One way of doing this is by an infinite geometric sequence of equilateral triangles in a spiral arrangement called the golden pentagon. However, if we want a tiling consisting of just a finite number of distinct tile types, we need to take a different approach. Following the method described in a previous note on non-periodic tilings, we seek a system of area equations with the characteristic cubic polynomial Q such that Q(x²) = −p(−x)p(x). This leads to

for which we have

From this we see that the trace of the system of area equations is 2, and since the area coefficients must be non-negative integers the only possibilities are 2+0+0 and 1+1+0. The first of these has no overall solution in non-negative integers, so the trace partition must be 1+1+0. Therefore, letting B, G, and Y denote the areas of the three distinct tile types, the system of area equations is of the form

In terms of the unknown coefficients the characteristic polynomial is

Identifying this polynomial with Q(λ), we have the conditions

The products of three coefficients in the second condition cannot both vanish, because each coefficient must be a non-negative integer, so the last two terms in the second condition could not equal 1. Consequently, the only solution (up to symmetry) is given by c₁₂ = c₂₃ = c₃₁ = 0 and c₂₁ = c₃₂ = c₁₃ = 1. Also, the dominant eigenvalue λ of the area equations is the square of the scale factor σ, so the area equations are

where σ = 1.3247179572447... is the root of p(σ) = σ³ − σ − 1. This implies that the inflated Blue tile is composed of one Blue and one Yellow tile. Also, the inflated Green tile is composed of one Blue and one Green tile. Lastly, the inflated Yellow tile is identical with the Blue tile.

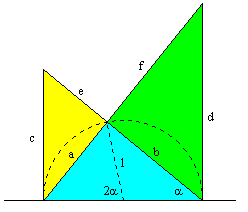
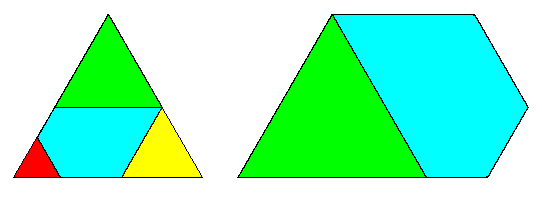
The G and Y tiles have the same shape, and we know that when G is appended to B it yields this same shape. In addition we know that when Y is appended to B it yields another figure similar to B. If these shapes are all triangles, they must all be similar right triangles, and we can arrange them schematically as shown below.

The necessary and sufficient condition for these shapes to combine in the required way is for the angle α to be such that b/2 = c/d. We have

and therefore

Substituting [1−cos(α)²]/cos(α)² for tan(α)² and clearing the denominator, we get

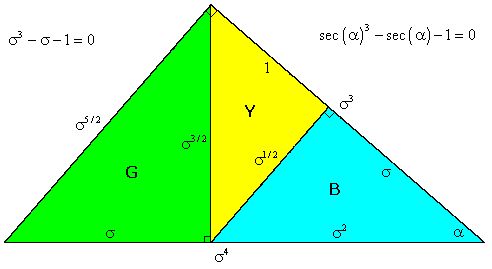
This shows that the secant (the reciprocal of the cosine) of α equals the scale factor σ, because it is the positive real root of the characteristic polynomial x³ − x − 1. The numerical value is α = 0.71532875... radians (about 40.985... degrees). Thus we arrive at the tiles given by three similar right triangles with the angles and edge lengths shown in the figure below.

Beginning with a single Blue tile, we can inflate by the factor s and sub-divide into one Blue and one Yellow tile. We can then inflate again, and the Yellow tile becomes a Green tile, and we can sub-divide the Blue tile into a Yellow and a Blue. And so on. If we let b_n, g_n, and y_n denote the numbers of Blue, Green, and Yellow tiles respectively on the nth stage, we have recurrences given by the transpose of the area equations, i.e.,

The numbers of tiles of the three types on the first several levels are shown below.

Each sequence individually satisfies the third order recurrence s_n = 2s_n−1 − s_n−2 + s_n−3, as well as the fourth order recurrence s_n = s_n−1 + s_n−2 + s_n−4, due to the factorization of the quartic

Asymptotically the terms increase by a factor of λ = σ² on each step, and we can see that y_n = b_n−1 and g_n = b_n−1 + b_n−3. Therefore, the fractions of tiles of each type as n goes to infinity approach

where T_n = b_n + g_n + y_n. Substituting σ² for λ and making use of the identity σ³ = σ + 1, these asymptotic ratios reduce to

These have the values 0.430159..., 0.324717..., and 0.245122... respectively. Equating the sum of these fractions to 1 gives the quartic noted above.

Incidentally, the cumulative sums of the b_n sequence give the g_n sequence, and the cumulative sums of the g_n sequence give values that are one less than the b_n sequence, so these two sequences are nearly the transform-duals of each other.

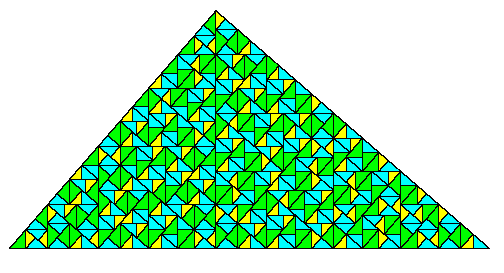
The figure below shows the tiling produced at the 11th stage, which consists of 200 Blue tiles, 151 Green tiles, and 114 Yellow tiles, in accord with the table given previously.

It's interesting to examine the variety of rectangular arrangements appearing in this tiling. The tiles do not all join "vertex-to-vertex", but there are only finitely many distinct edge junctions, and we could simply define additional vertices (with angles of π) along the edges so as to achieve vertex-to-vertex joining.

As an alternative to the inflation/partition method, these tilings can also be generated by constructing three sequences beginning with individual Blue, Green, and Yellow tiles respectively, and then combining them to produce the subsequent generations. Since the Green sequence is essentially just a copy of the Yellow, we really need only two sequences.

Another tiling based on Perrin's sequence can be constructed using equilateral triangles and golden pentagons. Each of these two shapes can be partitioned into smaller versions of the same shapes, as shown below.

The consecutive edges of the blue pentagons are in the ratio of 1 : σ : σ² : σ³ : σ⁴ :σ⁵, where σ is the real root of x³ − x − 1 = 0. If we let T_j for j = 1,2,..,5 denote an equilateral triangle with edge length σ^j, and P a golden pentagon with smallest edge length 1, then by partition and inflation we have the substitutions

Beginning with a single T₅ tile, the numbers of the various tile types after n stages of inflation and partition are given by

The characteristic polynomial of this equation is

The first factor is just the "inverse" of Perrin's polynomial (i.e., it has the reciprocal roots), and the second factor is the same as the polynomial Q(λ) discussed previously. In other words, Q(x²) = −p(−x)p(x) where p is Perrin's polynomial. After ten stages of inflation and partition, we arrive at the arrangement of 469 tiles shown below.

This contains 45 tiles of type T₁ (dark green), 28 of type T₂ (light blue), 60 of type T₃ (red), 144 of type T₄ (light green), 84 if type T₅ (yellow), and 108 of type P (dark blue). The asymptotic numbers of tiles of these types are proportional to σ², 1, σ³, σ⁶, σ⁴, and σ⁵ respectively, and thus the total number of tiles is proportional to 4 + 5σ + 4σ².

Return to MathPages Main Menu